Аристотелева силлогистика и логика предикатов

В предыдущем пункте показано как аристотелевы силлогизмы переводятся на язык логики предикатов: каждому силлогизму сопоставляется формула логики предикатов, при этом правильным силлогизмам соответствуют тавтологии (общезначимые формулы) логики предикатов, а неправильным силлогизмам — формулы, не являющиеся тавтологиями.

Тем не менее при более пристальном рассмотрении этих формул выясняется, что так происходит не для всех правильных аристотелевых силлогизмов: тавтологии соответствуют лишь пятнадцати из них. Остальным четырем правильным силлогизмам Darapti, Felapton, Bramantip и Fesapo соответствуют формулы логики предикатов, не являющиеся общезначимыми, т.е. тавтологиями.

Пример 24.10. Рассмотрим формулу, отвечающую силлогизму Darapti:

Покажем, что эта формула не является общезначимой. Для этого нужно указать такие конкретные предикаты , заданные над некоторым множеством , что посылка силлогизма превратится в истинное высказывание

, А следствие — в ложное .

Для этого достаточно, чтобы предикат был тождественно ложен, а предикаты и обладали бы тем свойством, что для любого предмета одно из высказываний или было бы ложным. Последнее возможно, если, например, один из предикатов или является отрицанием другого. Укажите самостоятельно примеры таких предикатов, например, на множестве натуральных чисел .

Выпишите самостоятельно формулы логики предикатов для оставшихся трех "плохих" силлогизмов и докажите, что они не общезначимы. Выпишите также формулы логики предикатов для пятнадцати "хороших" аристотелевых силлогизмов и докажите их общезначимость.

Какой же вывод можно сделать после анализа результатов перевода аристотелевых силлогизмов на язык логики предикатов? Вывод таков, что логика предикатов, как и алгебра высказываний, далеко не является совершенной математической теорией, отражающей (описывающей) процесс человеческого мышления. И эта теория допускает изъяны, приводит к выводам, не сопоставимым с результатами реальных процессов, которые теория призвана описать. Это же обстоятельство приводит, с одной стороны, к задаче создания аксиоматической теории аристотелевых силлогизмов, в которой каждый верный силлогизм по каким-то правилам выводился бы из аксиом, а с другой — к задаче построения такой логической системы, которая все же вписывала бы всю традиционную силлогистику в общий ансамбль современной формальной логики. Эти вопросы будут рассмотрены в следующих лекциях.

Теоретико-множественная интерпретация аристотелевой силлогистики

Данная интерпретация, в частности, поможет лучше понять причину того, что не все верные силлогизмы выражаются на языке логики предикатов общезначимой формулой. Обозначим множества истинности предикатов через соответственно. Тогда утверждения об истинности категорических суждений могут быть следующим образом выражены на теоретико-множественном языке (учитывайте запись этих утверждений на языке логики предикатов, мы говорили уже об этом выше):

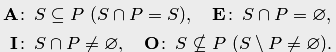
Нетрудно изобразить с помощью диаграмм Эйлера–Венна взаимоотношения между множествами и в каждом случае:

Теперь каждый аристотелев силлогизм будет представлять собой утверждение о том, что из каких-то двух соотношений между множествами непременно следует третье соотно

шение между множествами и .

Пример 24.11. Например, силлогизм Bocardo на теоретико-множественном языке запишется так:

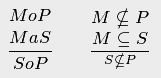
Используя свойства отношения включения , нетрудно установить справедливость данного силлогизма. В самом деле, допустим, что он несправедлив, т. е. , но . Тогда из второго и третьего условий, в силу транзитивности отношения с, заключаем, что , а это противоречит первому условию.

Пример 24.12. Пример верного силлогизма Fresison. Его запись:

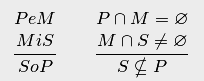
Предположим, что . Тогда . Учитывая это, находим:

(неравенство на основании второго условия). Следовательно, , что противоречит первому условию.

Пример 24.13. Приведем пример неправильного силлогизма:

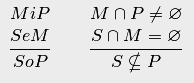
Диаграмма показывает, что для трех множеств возможна ситуация, когда условия выполнены: , а заключение — нет: . Следовательно, данный силлогизм неверен, т.е. рассуждения по данной схеме неправильны.

Наконец обратимся к четырем "плохим" с точки зрения логики предикатов правильным силлогизмам Darapti, Felaption, Bramantip и Fesapo и постараемся понять, почему выражающие их формулы логики предикатов оказались необщезначимыми.