Приложение алгебры высказываний к доказательству теорем

Прямая и обратная теоремы

Многие математические теоремы имеют структуру, выражаемую формулой . Утверждение называется условием теоремы, а утверждение — ее заключением.

Например: "Если в четырехугольнике все стороны равны между собой , то его диагонали перпендикулярны ". Символическая запись этой теоремы: .

Рассмотрим еще такой пример: "Если один из углов треугольника прямой , то квадрат длины одной из сторон этого треугольника равен сумме квадратов длин двух других его сторон ". Символически: .

Тщательный анализ теоремы позволяет выявить в ней более сложную структуру: условие представляет собой дизъюнкцию трех утверждений , где высказывание есть " ", высказывание есть " " и высказывание — " " (символами обозначены величины углов треугольника). Аналогично, заключение также представляет собой дизъюнкцию трех утверждений: , где — высказьшание " ", — высказывание " ", — высказывание " " (символами обозначены длины сторон треугольника, лежащие против углов величины соответственно). Таким образом, теорема при более пристальном рассмотрении имеет вид

Далее, если некоторая теорема имеет форму , утверждение называется обратным для данной теоремы. Это утверждение может быть справедливым, и тогда оно называется теоремой, обратной для теоремы , которая, в свою очередь, называется прямой теоремой. Если же утверждение не выполняется, то говорят, что обратная теорема для теоремы неверна. Так, для теоремы обратная теорема неверна, а для теоремы справедлива обратная теорема (проверьте!). Таким образом, при доказательстве теоремы нужно четко выделять, каково ее условие и что доказывается. Доказательство прямой теоремы не дает оснований для вывода о том, что и обратная теорема также верна. Обратная теорема требует специальной проверки. Это обусловлено тем, что формулы и , выражающие структуры прямой и обратной теорем, не равносильны, в чем мы убедились на приведенных примерах. Их неравносильность можно усмотреть также из таблиц истинности данных формул.

Структура теоремы достаточно проста. Рассмотрим теорему более сложной структуры: "В равных треугольниках против равных углов лежат равные стороны". Чтобы четко выделить условие данной теоремы и заключение, сформулируем ее следующим образом: "Если два треугольника равны , то из попарного равенства двух углов этих треугольников следует равенство их противолежащих сторон ". Символически теорема записывается так: , т. е. она имеет строение, описываемое формулой . На основании равносильности, получающейся из тавтологии теоремы (правило перестановки посылок), данная формула равносильна формуле , а на основании равносильности— правило объединения и разъединения посылок) она равносильна формуле . Следовательно, теорема может быть сформулирована в виде

"Если два угла двух треугольников попарно равны , то из равенства этих треугольников следует равенство сторон, противолежащих этим углам ".

Наконец, третий вид данной теоремы :

"Если треугольники равны и в них два угла попарно равны , то и противолежащие стороны равны ".

Таким образом, условие этой теоремы состоит из двух утверждений и или представляет собой их конъюнкцию , а заключением является утверждение .

Если теперь зададимся целью сформулировать теорему, обратную рассмотренной теореме , то столкнемся с некоторыми трудностями, преодолеть которые помогает алгебра высказываний. Обратная теорема — такая, в которой условие и заключение прямой теоремы поменялись местами. В рассматриваемой прямой теореме два условия и одно заключение. Это приводит к тому, что получается не одна обратная теорема, а несколько. Так, обращение первых трех форм данной теоремы приводит к следующим обратным утверждениям:

1) "Если из попарного равенства двух углов треугольников следует равенство их противолежащих сторон, то такие треугольники равны";

2) "Если отрезки обладают тем свойством, что, будучи сторонами в равных треугольниках, они лежат против равных углов, то эти отрезки равны";

3) "Если сторона одного треугольника равна стороне другого треугольника, то треугольники равны и углы, противолежащие этим сторонам, также равны".

Необходимые и достаточные условия

С понятиями прямой и обратной теорем тесно связан вопрос о необходимых и достаточных условиях. Если некоторая математическая теорема имеет структуру, выражаемую формулой , то высказывание называется необходимым условием для высказывания (другими словами, если истинно, то с необходимостью должно быть также истинным), а высказывание называется достаточным условием для высказывания (другими словами, для того чтобы было истинным, достаточно, чтобы истинным было высказывание ). Посмотрим с этой точки зрения на первую теорему . Необходимым условием равенства в четырехугольнике всех сторон является перпендикулярность его диагоналей. Иначе говоря, достаточным условием для перпендикулярности диагоналей четырехугольника является равенство всех его четырех сторон.

Одно и то же утверждение может иметь несколько необходимых условий. Так, необходимыми условиями равенства всех сторон четырехугольника являются, кроме указанного, деление диагоналей точкой их пересечения пополам , деление диагоналями соответствующих углов пополам и т.д. Аналогично, одно и то же утверждение может иметь несколько достаточных условий. Так, для перпендикулярности диагоналей четырехугольника достаточно также, чтобы в нем было две пары равных смежных сторон.

После того как доказана теорема , возникает вопрос, будет ли найденное необходимое условие достаточным или достаточное — необходимым. Иначе говоря, будет ли верно утверждение , называемое обратным по отношению к теореме . Известно, что условие перпендикулярности диагоналей четырехугольника , необходимое для равенства всех его сторон , не будет достаточным для такого равенства. Для проверки нужно привести пример четырехугольника с перпендикулярными диагоналями, у которого не все стороны равны (сделайте это!).

Если справедливы утверждения и , т. е. справедливо , то считают, что — необходимое и достаточное условие для , и, наоборот, что — необходимое и достаточное условие для , или же что является критерием (для) . Математическая наука изобилует утверждениями вида , представляющими собой необходимые и достаточные условия, и их приходится отыскивать в самых разных ее областях. Происходит это приблизительно следующим образом. Предположим, требуется найти необходимое и достаточное условие для некоторого утверждения . Начинают с отыскания ряда необходимых условий для , т.е. утверждений , следующих из . При этом каждый раз пытаются анализировать, не окажется ли то или иное найденное условие или какая-либо их совокупность (конъюнкция) достаточным условием для , т. е. окажется ли истинной какая-либо из импликаций:

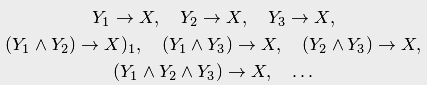
Так, в примере с четырехугольником имеем два необходимых условия и для свойства , т.е. верны две теоремы: и . Затем, если ни одно из необходимых условий в отдельности не является достаточным (именно такая ситуация в данном примере), то пытаются проверять на достаточность всевозможные конъюнкции этих условий. Так, в указанном примере справедливо следующее утверждение: . (Убедитесь в этом самостоятельно.) Поэтому конъюнкция является достаточным условием для свойства .

Рассмотрим еще один пример.

Пример 7.1. Пусть требуется найти необходимое и достаточное Условие того, что выпуклый четырехугольник является квадратом . Находим ряд необходимых условий для этого утверждения:

"Диагонали четырехугольника перпендикулярны"; "Диагонали четырехугольника равны"; "Диагонали четырехугольника точкой пересечения делятся пополам".

Ясно, что каждое из утверждений верно. Анализируем обратные утверждения. Только соединение (конъюнкция) всех трех необходимых для условий дает условие, достаточное для . Это "Диагонали четырехугольника перпендикулярны, равны и делятся пополам точкой их пересечения". Таким образом, истинно утверждение . Кроме того, из истинности утверждений вытекает истинность утверждения . Итак, необходимым и достаточным условием для является условие .