
- •Инструкция по exel
- •Возможности excel
- •1. Организация и принцип действия электронных таблиц
- •2. Оформление таблицы
- •Очень удобно при редактировании таблицы применять команды контекстного меню, которое вызывается правой кнопкой мыши.
- •3. Функции и вычисления ( логические, табличные, матричные функции )
- •Логическая функция если имеет три аргумента и позволяет по условию выбирать различные пути решения. Её синтаксис: если ( лог_выраж; значение1_если_истина; значение2_если_ложь )
- •Табличные функции предназначены для обработки данных одной или нескольких таблиц. В данном разделе рассматриваются функции впр, гпр, частота и ранг.
- •4. Функции и вычисления
- •Практическая работа № 4. Применяю теорию на практике:
- •Практическое задание № 5. Операции со списками:
- •Макропрограммирование.
- •Практическая работа № 6.
Логическая функция если имеет три аргумента и позволяет по условию выбирать различные пути решения. Её синтаксис: если ( лог_выраж; значение1_если_истина; значение2_если_ложь )
Смысл (семантику) данной функции можно пояснить следующим образом:
если логическое_выражение (1-й аргумент) - истина, то результатом будет значение1_если_истина (2-й аргумент), иначе – значение2_если_ложь (3-й аргумент).
Любое логическое выражение (“высказывание”) может иметь одно из двух значений: TRUE (истина) или FALSE (ложь). В качестве логических выражений используются
- логические отношения два арифметических выражения, соединенные символом операции отношения, например, x > k-1; это самые простые логические выражения;
- логические одночлены - два или более логических отношения, соединенные логической операцией "И": x > 10 И x < 15 ( "х лежит между 10 и 15"); эту операцию называют также логическим умножением; в Еxcel эти выражения записываются по-другому (в префиксной форме) символ логической операции находится перед аргументами): И (x > 10; x < 15) ;
- логические многочлены - два или более логических одночлена, соединенные операцией "ИЛИ": ИЛИ ( x=2; y=2; z=2 ) - т.е. "хотя бы одна из трех переменных - x, y, z - равна 2" .
Пример использования функции ЕСЛИ в одном из вариантов расчёта подоходного налога: =ЕСЛИ ( C4>1000000; 20%*C4; 12%*С4) ; здесь функция ЕСЛИ выдаёт два возможных результата в зависимости от оклада. Если в качестве 3-го аргумента функции ЕСЛИ использовать эту же функцию, то можно получить 3 пути решения: = ЕСЛИ ( Х>10; формула1; ЕСЛИ (X<5; формула2; форм.3)).
В этой же формуле на место формулы3 можно вставить еще одну функцию ЕСЛИ и выполнить вычисления по 4 формулам и т.д. (но не более 7). Функция ЕСЛИ неявно применяется в других вычислениях, например, в функциях СУММЕСЛИ и СЧЁТЕСЛИ , вычисляющих сумму или количество лишь тех значений, которые удовлетворяют заданному условию.
Табличные функции предназначены для обработки данных одной или нескольких таблиц. В данном разделе рассматриваются функции впр, гпр, частота и ранг.
Функции ВПР (вертикальный просмотр таблиц по столбцам) и ГПР (горизонтальный по строкам) позволяют сопоставить данные двух таблиц основной и вспомогательной (справочной). Справочные таблицы содержат граничные значения диапазонов, а основные произвольные значения, каждое из которых должно быть отнесено к одному из диапазонов.
Функция РАНГ возвращает ранг значений в списке значений (их порядковые номера относительно других значений). Например, тестируемых можно распределить по местам, задав 1 тому, кто набрал наибольшее количество баллов, 2 – для второго места и т.д. Функция имеет 3 аргумента: число в первой ячейке столбца исходных данных; ссылка на весь исходный столбец в абсолютной адресации; порядок (0 по возрастанию ранга, 1 по убыванию).
Функция ЧАСТОТА (исходный массив; массив карманов) подсчитывает, сколько значений из исходного массива попадают в диапазоны значений, представленных в массиве карманов. Если массив карманов содержит числа {a, b, c}, то числа исходного массива распределяются по интервалам: (-¥, a], (a, b], (b, c], (c, ¥). Таким образом, количество промежутков на 1 больше элементов в массиве карманов. Прежде чем использовать функцию ЧАСТОТА, выделяют свободный массив ячеек, на единицу больший чем массив карманов, и вводят функцию ЧАСТОТА. За исходный массив можно взять массив ячеек в любом столбце таблицы Табл1, за массив карманов – значения из столбца Сумма баллов справочной таблицы Табл2 (в абсолютных адресах). Затем щелчок в строке формул и завершение операции одновременным нажатием Ctrl+Shift+Enter (не ОК).
Матричные функции предназначены для обработки двумерных массивов данных матриц, которые широко применяются для решения математических задач. В Excel это функции категории Математические: МОПРЕД – вычисление определителя матрицы, МОБР – вычисление обратной матрицы, МУМНОЖ – перемножение матриц, и в категории Ссылки и массивы ТРАНСП – транспонирование матрицы. Функция МОПРЕД возвращает число, поэтому вводится как обычная формула. Остальные функции (а также операции поэлементной обработки матриц одинакового размера) формируют блок ячеек, поэтому они вводятся как массивы. При обработке матриц удобно вводить имена для массивов данных. Так, например, если две матрицы введены в блоки А1:С2 и Е1:G2 и этим блокам присвоены имена М и N, то формула поэлементного сложения матриц будет иметь простой и понятный вид: =M+N (набор формулы завершается групповой операцией ввода).
Ф
![]()
![]()
Для решения системы уравнений её представляют в матричном виде: АХ=В, где А матрица коэффициентов при неизвестных, Х массив неизвестных, В массив свободных членов. Если определитель матрицы не равен нулю, то решение системы можно получить путём перемножения обратной матрицы A-1 на массив В (с применением функции МУМНОЖ).
Практическая работа № 3. В данной работе я должна была вставить формулы расчета среднего балла для каждого студента, по каждому предмету и общего по всем предметам (добавив итоговую строку); ввести в последний столбец формулу с функцией ЕСЛИ, вычисляющую следующие текстовые значения: ОТЛ для студентов, имеющих только “5”, ХОР"4" и "5", УД "3", "4", "5" и НЕУД "2" , "3", "4", 5"; посчитать сумму баллов для каждого ученика; подсчитать в новых ячейках (с пояснениями) количество отличников и неуспевающих:
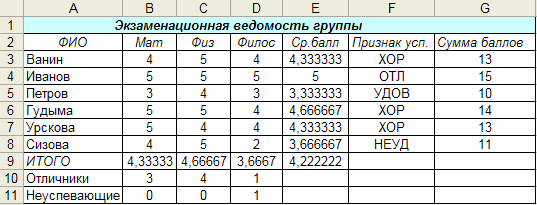
Мои действия:
1.
 2.
2.

3.

4.
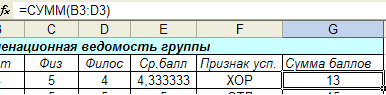
5.
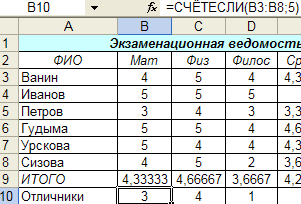 6.
6.
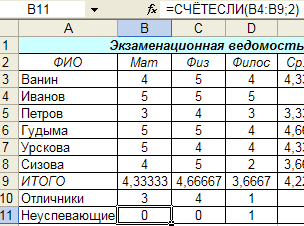
Также я выполнила
обработку табличных данных с использованием
функций ВПР, ЧАСТОТА и РАНГ:
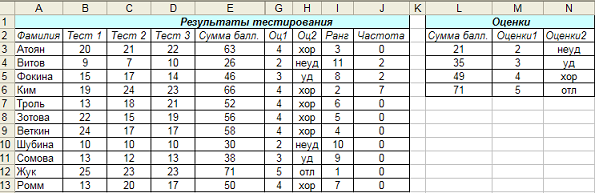
Мои действия:
1.
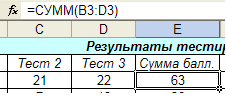 2.
2.
3. 4.
4.
5.
Также нужно было применить матричные функции:

Мои действия:
1.
 2.
2.
3. 4.
4.
5. 6.
6.
7.
