Министерство образования и науки Российской Федерации ФГБОУ ВПО «Поволжский государственный технологический университет»

Кафедра РТ и МБС

Курсовая работа

«Опыт Нернста. Анализ формулы Нернста. Работы В. Освальда. Расчет потенциала Нернста»

Выполнил: ст. гр. БТС-31

Мосунов А.В.

Проверил: д.т.н., профессор

Фурман Я.А.

Йошкар-Ола

2014 г.

Содержание

1. Цель работы……………...………………………………….3

2. Опыт Нернста………………………….……………………4

3. Анализ формулы Нернста…………………………………5

4. Расчет потенциала Нернста ……………………………….8

5. Работа Вильгельма Освальда …………………………......11

6. Заключение…………………………………………………13

7. Список литературы……………………………………..…..14

Целью курсовой работы является изучение работы Вальтера Нернста и Вильгельма Освальда.

Опыт Нернста

        Закон распределения определяет относительное содержание в двух несмешивающихся или ограниченно смешивающихся жидкостях растворимого в них компонента; является одним из законов идеальных разбавленных растворов. Открыт в 1890 Вильгельмом Нернстом. Согласно Нернста закон распределения, при равновесии отношение концентраций третьего компонента в двух жидких фазах является постоянной величиной. Нернстом закон распределения может быть записан в виде c₁/c₂ = k, где c₁и c₂ — равновесные молярные концентрации третьего компонента в первой и второй фазах; постоянная k — коэффициент распределения, зависящий от температуры. Его закон позволяет определить более выгодные условия экстрагирования веществ из растворов.

Анализ формулы Нернста

Третье начало термодинамики (теорема Нернста) – физический принцип, определяющий поведение энтропии при приближении температуры к абсолютному нулю. Является одним из постулатов термодинамики, принимаемым на основе обобщения значительного количества экспериментальных данных.

Третье начало термодинамики может быть сформулировано так:

«Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система».

или

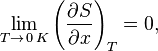
где  – любой термодинамический параметр.

Третье начало термодинамики относится только к равновесным состояниям.

Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение):

,

Третье начало термодинамики может быть использовано для точного определения энтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю.

Третье начало термодинамики позволяет находить абсолютное значение энтропии, что нельзя сделать в рамках классической термодинамики (на основе первого и второго начал термодинамики). В классической термодинамике энтропия может быть определена лишь с точностью до произвольной аддитивной постоянной , что не мешает термодинамическим исследованиям, так как реально измеряется разность энтропий в различных состояниях. Согласно третьему началу термодинамики, при значение .

В 1911 году Макс Планк сформулировал третье начало термодинамики как условие обращения в нуль энтропии всех тел при стремлении температуры к абсолютному нулю: . Отсюда , что даёт возможность определять абсолютное значения энтропии и других термодинамических потенциалов. Формулировка Планка соответствует определению энтропии в статистической физике через термодинамическую вероятность состояния системы . При абсолютном нуле температуры система находится в основном квантово-механическом состоянии. Если оно невырожденно, то (состояние реализуется единственным микрораспределением) и энтропия при равна нулю. В действительности при всех измерениях стремление энтропии к нулю начинает проявляться значительно раньше, чем могут стать существенными дискретность квантовых уровней макроскопической системы и влияние квантового вырождения.