
- •3) Эквипотенциальные поверхности. Связь между напряженностью и разностью потенциалов.
- •2)Строение Атомного Ядра
- •Элементом называется вещество, состоящее из атомов с одинаковым зарядом ядра.
- •Элемент – это вещество, которое при химическом превращении всегда увеличивает свой вес.
- •3)Ядерные Силы
- •4)Энергия Связи Ядра
Билет по Физике №26
Вопрос Работа сил Электрического Поля
При
перемещении пробного заряда q в
электрическом поле электрические силы
совершают работу. Эта работа при малом
перемещении ![]() равна
(рис. 1.4.1):
равна
(рис. 1.4.1):
|
-

Рисунок 1.4.1.
Работа электрических сил при малом перемещении заряда q
Рассмотрим работу сил в электрическом поле, создаваемом неизменным во времени распределенным зарядом, т.е. электростатическом поле
Электростатическое поле обладает важным свойством:
Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Аналогичным свойством обладает и гравитационное поле, и в этом нет ничего удивительного, так как гравитационные и кулоновские силы описываются одинаковыми соотношениями.
Следствием независимости работы от формы траектории является следующее утверждение:
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Силовые поля, обладающие этим свойством, называют потенциальными или консервативными.
На рис. 1.4.2 изображены силовые линии кулоновского поля точечного заряда Q и две различные траектории перемещения пробного заряда q из начальной точки (1) в конечную точку (2). На одной из траекторий выделено малое перемещение
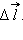 Работа
ΔA кулоновских
сил на этом перемещении равна
Работа
ΔA кулоновских
сил на этом перемещении равна 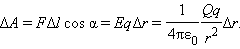
Таким образом, работа на малом перемещении зависит только от расстояния r между зарядами и его изменения Δr. Если это выражение проинтегрировать на интервале от r = r1 до r = r2, то можно получить
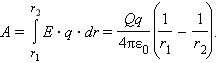
-
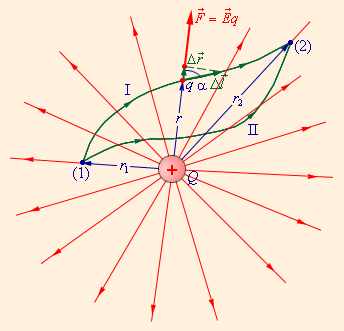
Рисунок 1.4.2.
Работа кулоновских сил при перемещении заряда qзависит только от расстояний r1 и r2 начальной и конечной точек траектории
Полученный результат не зависит от формы траектории. На траекториях I и II, изображенных на рис. 1.4.2, работы кулоновских сил одинаковы. Если на одной из траекторий изменить направление перемещения заряда q на противоположное, то работа изменит знак. Отсюда следует, что на замкнутой траектории работа кулоновских сил равна нулю.
Если электростатическое поле создается совокупностью точечных зарядов
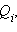 то
при перемещении пробного
заряда q работа A результирующего
поля в соответствии с принципом
суперпозиции будет
складываться из работ
то
при перемещении пробного
заряда q работа A результирующего
поля в соответствии с принципом
суперпозиции будет
складываться из работ  кулоновских
полей точечных зарядов:
кулоновских
полей точечных зарядов: 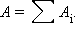 Так
как каждый член суммы
не
зависит от формы траектории, то и полная
работа A результирующего
поля не зависит от пути и определяется
только положением начальной и конечной
точек.
Так
как каждый член суммы
не
зависит от формы траектории, то и полная
работа A результирующего
поля не зависит от пути и определяется
только положением начальной и конечной
точек.Свойство потенциальности электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. Для этого в пространстве выбирается некоторая точка (0), и потенциальная энергия заряда q, помещенного в эту точку, принимается равной нулю.
Потенциальная энергия заряда q, помещенного в любую точку (1) пространства, относительно фиксированной точки (0) равна работе A10, которую совершит электростатическое поле при перемещении заряда q из точки (1) в точку (0):
Wp1 = A10.
(В электростатике энергию принято обозначать буквой W, так как буквой E обозначают напряженность поля.)
Так же, как и в механике, потенциальная энергия определена с точностью до постоянной величины, зависящей от выбора опорной точки (0). Такая неоднозначность в определении потенциальной энергии не приводит к каким-либо недоразумениям, так как физический смысл имеет не сама потенциальная энергия, а разность ее значений в двух точках пространства.
Работа, совершаемая электростатическое полем при перемещении точечного заряда q из точки (1) в точку (2), равна разности значений потенциальной энергии в этих точках и не зависит от пути перемещения заряда и от выбора точки (0).
A12 = A10 + A02 = A10 – A20 = Wp1 – Wp2.
Потенциальная энергия заряда q, помещенного в электростатическое поле, пропорциональна величине этого заряда.
Физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
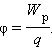
Потенциал φ является энергетической характеристикой электростатического поля.
Работа A12 по перемещению электрического заряда q из начальной точки (1) в конечную точку (2) равна произведению заряда на разность потенциалов (φ1 – φ2) начальной и конечной точек:
A12 = Wp1 – Wp2 = qφ1 – qφ2 = q(φ1 – φ2).
В Международной системе единиц (СИ) единицей потенциала является вольт (В).
1 В = 1 Дж / 1 Кл.
Во многих задачах электростатики при вычислении потенциалов за опорную точку (0) удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом:
Потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
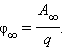
Потенциал φ∞ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
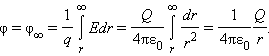
Как следует из теоремы Гаусса, эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R, где R – радиус шара.
Для наглядного представления электростатическое поля наряду с силовыми линиями используют эквипотенциальные поверхности.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью илиповерхностью равного потенциала.
Силовые линии электростатическое поля всегда перпендикулярны эквипотенциальным поверхностям.
Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы. На рис. 1.4.3 представлены картины силовых линий и эквипотенциальных поверхностей некоторых простых электростатических полей.
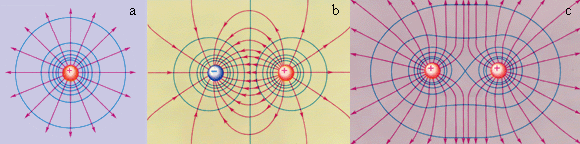
Рисунок 1.4.3.
Эквипотенциальные поверхности (синие линии) и силовые линии (красные линии) простых электрических полей: a – точечный заряд; b – электрический диполь; c – два равных положительных заряда
В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей.
Если пробный заряд q совершил малое перемещение вдоль силовой линии из точки (1) в точку (2), то можно записать:
ΔA12 = qEΔl = q(φ1 – φ2) = – qΔφ,
где Δφ = φ1 – φ2 – изменение потенциала. Отсюда следует

Это соотношение в скалярной форме выражает связь между напряженностью поля и потенциалом. Здесь l – координата, отсчитываемая вдоль силовой линии.
Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов:
φ = φ1 + φ2 + φ3 + ... |
2) Потенциал и разность потенциалов
Потенциал. Разность потенциалов. Напряжение. |
|
Потенциал электростатического
поля — скалярная величина, равная
отношению потенциальной энергии
заряда в поле к этому заряду: - энергетическая характеристика поля в данной точке. Потенциал не зависит от величины заряда, помещенного в это поле. |
|
Т.к. потенциальная энергия зависит от выбора системы координат, то и потенциал определяется с точностью до постоянной. За точку отсчета потенциала выбирают в зависимости от задачи: а) потенциал Земли, б) потенциал бесконечно удаленной точки поля, в) потенциал отрицательной пластины конденсатора. |
|
- следствие принципа суперпозиции полей (потенциалы складываютсяалгебраически). |
|
Потенциал численно равен работе поля по перемещению единичного положительного заряда из данной точки электрического поля в бесконечность. В
СИ потенциал измеряется в вольтах: |
|
Разность потенциалов |
|
|
|
Напряжение — разность значений потенциала в начальной и конечнойточках траектории. Напряжение численно равно работе электростатического поля при перемещении единичного положительного заряда вдоль силовых линий этого поля. Разность потенциалов (напряжение) не зависит от выбора системы координат! |
|
Единица разности потенциалов
Напряжение равно 1 В, если при перемещении положительного заряда в 1 Кл вдоль силовых линий поле совершает работу в 1 Дж. |
|
Связь между напряженностью и напряжением. |
|
Из
доказанного выше: напряженность равна градиенту потенциала (скорости изменения потенциала вдоль направления d). |
|
Из этого соотношения видно:
|
|
Эквипотенциальные поверхности. ЭПП - поверхности равного потенциала. Свойства ЭПП: - работа при перемещении заряда вдоль эквипотенциальной поверхности не совершается; - вектор напряженности перпендикулярен к ЭПП в каждой ее точке. |
|
|
|
Измерение электрического напряжения (разности потенциалов) Между стержнем и корпусом — электрическое поле. Измерение потенциала кондуктора Измерение напряжения на гальваническом элементе Электрометр дает большую точность, чем вольтметр. |
|
Потенциальная энергия взаимодействия зарядов. |
|
|
|
Потенциал поля точечного заряда |
|
|
|
Потенциал заряженного шара а) Внутри шара Е=0, следовательно, потенциалы во всех точках внутри заряженного металлического шара одинаковы (!!!) и равны потенциалу на поверхности шара. б) Снаружи поле шара убывает обратно пропорционально расстоянию от центра шара, как и в случае точечного заряда. |
|
Перераспределение зарядов при контакте заряженных проводников. Переход зарядов происходит до тех пор, пока потенциалы контактирующих тел не станут равными. |
|
3) Эквипотенциальные поверхности. Связь между напряженностью и разностью потенциалов.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью.
Между
двумя любыми точками на эквипотзенциальной
поверхности разность потенциалов равна
нулю, поэтому работа сил электрического
поля при любом перемещении заряда по
эквипотенциальной поверхности равна
нулю. Это означает, что вектор силы ![]() в
любой точке траектории движения заряда
по эквипотенциальной поверхности
перпендикулярен вектору скорости.
Следовательно, линии напряженности
электростатического поля перпендикулярны
эквипотенциальной поверхности.
в
любой точке траектории движения заряда
по эквипотенциальной поверхности
перпендикулярен вектору скорости.
Следовательно, линии напряженности
электростатического поля перпендикулярны
эквипотенциальной поверхности.
Эквипотенциальными поверхностями поля точечного электрического заряда являются сферы, в центре которых расположен заряд (рис. 112).
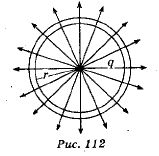
Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные линиям напряженности (рис. 113).

Напряжённость, силовая характеристика поля, и разность потенциалов, его энергетическая характеристика, связаны однозначно. Вычислим работу поля при малом перемещении заряда двумя способами: A=qEΔlcosα=qElΔl;где α - угол между векторами напряжённости и перемещения, El - проекция напряжённости на перемещение. A=-qΔφ. Приравнивая, получаем: ElΔl=-Δφ=U. Зная напряжённость в каждой точке, можно вычислить разность потенциалов между любыми точками. Зная разность потенциалов между любыми точками, можно вычислить проекцию напряжённости на направление между ними. El=-Δφ/Δl=U/Δl. Отсюда следует,что напряжённость направлена в сторону убывания потенциала. Эта формула позволяет также определить вторую единицу напряжённости - вольт на метр (В/м). 1В/м=1Н/Кл.
При перемещении заряда под прямым углом к линиям напряжённости работа поля равна нулю, так как сила перпендикулярна перемещению. Следовательно, все точки поверхности, перпендикулярной в каждой точке линиям напряжённости имеют одинаковый потенциал. Такие поверхности называют эквипотенциальными. Эквипотенциальные поверхности, как и силовые линии, позволяют наглядно представить электрическое поле.
Эквипотенциальные поверхности однородного поля - параллельные плоскости, точечного заряда - концентрические сферы. Поверхность любого проводника является эквипотенциальной, так как напряжённость направлена перпендикулярно ей. Потенциал всех точек внутри проводника одинаков, потому что, раз напряжённость поля в проводнике равна нулю, то равна нулю и разность потенциалов.
Разность потенциалов и напряжённость являются количественными характеристиками поля. Напряжённость более наглядна и указывает направление силы, действующей на заряд. Но разность потенциалов тоже имеет свои преимущества. Разность потенциалов легче измерить, чем напряжённость. Потенциал - скаляр, поэтому задаётся одним числом, а напряжённость - вектор, поэтому задаётся тремя числами - проекциями на оси кооординат. Многие процессы и величины (например, сила тока) определяются не силой, действующей со стороны поля, а его энергией и работой, то есть разностью потенциалов.
Билет по Физике №26 (2 Вопрос)
1. Атомное ядро – связанная система нейтронов и протонов Атомное ядро – центральная и очень компактная часть атома, в которой сосредоточена практически вся его масса и весь положительный электрический заряд. Ядро, удерживая вблизи себя кулоновскими силами электроны в количестве, компенсирующем его положительный заряд, образует нейтральный атом. Большинство ядер имеют форму, близкую к сферической. Ядро имеет размер ≈ 10-12 см, что на четыре порядка меньше размера атома (10-8 см).Плотность вещества в ядре – около 230 млн. тонн/см3. Атомное ядро было открыто в 1911 г. в результате серии экспериментов по рассеянию α-частиц тонкими золотыми и платиновыми фольгами, выполненных в Кембридже (Англия) под руководствомЭ. Резерфорда. Оказалось, что угловое распределение α-частиц, рассеянных на атоме, имеет вид
где
Zα -
электрический заряд α-частицы, Zядра –
электрический заряд ядра, E – кинетическая
энергия α-частицы, θ – угол рассеяния
α-частицы.
Это означало,
что в атоме имеется точечное положительно
заряженное ядро, содержащее в себе
практически всю массу ядра. В 1914 году
Э.Резерфорд показал, что в состав
атомного ядра входят протоны – ядра
атома водорода.
В 1932 г.
после открытия Дж.Чедвиком нейтрона
стало ясно, что ядро состоит из протонов
и нейтронов
(В. Гейзенберг, Д.Д. Иваненко, Э. Майорана).
Атомные ядра представляют собой
квантовые системы нуклонов, связанных
между собой ядерным взаимодействием.
Свойства атомных ядер определяются
совместным действием сильных,
электромагнитных и слабых
взаимодействий.
Атомные ядра состоят из нейтронов n и
протонов p. Свойства свободных нейтрона
и протона приведены в Табл. 1.
Для обозначения атомного ядра
используется символ химического
элемента атома, в состав которого
входит ядро. Левый верхний индекс у
этого символа показывает суммарное
число нейтронов и протонов в данном
ядре, а левый нижний – число протонов
в нём. Например, ядро никеля, содержащее
58 нуклонов, из которых 28 протонов,
обозначается Таблица 1. Свойства свободных нейтрона и протона
Ядерное взаимодействие (взаимодействие между нуклонами в ядре) возникает за счёт того, что нуклоны обмениваются мезонами. Это взаимодействие – проявление более фундаментального сильного взаимодействия между кварками, из которых состоят нуклоны и мезоны. Мир ядер очень разнообразен. Известно около 3500 ядер, отличающихся друг от друга либо числом протонов, либо числом нейтронов, либо тем и другим. Большинство из них получено искусственным путём. 264 ядра стабильны, т.е. не испытывают со временем никаких самопроизвольных превращений. Остальные ядра испытывают различные виды радиоактивного распада – альфа-распад (испускание альфа-частицы, т.е. ядра атома гелия); бета-распад (одновременное испускание – электрона и антинейтрино или позитрона и нейтрино, а также поглощение атомарного электрона с испусканием нейтрино); гамма-распад (испускание фотона), деление и другие. Простейшим приближением распределения ядерной материи является распределение Ферми (рис. 1).
где ρ0 - плотность ядерной материи в центре ядра, R - радиус ядра (расстояние от центра ядра, на котором плотность ядерной материи спадает в два раза), t – толщина поверхностного слоя ядра (расстояние, на котором плотность ядерной материи спадает от 0.9ρ0 до 0.1ρ0). Параметры a и t связаны соотношением t ≈ 4.4a.
Для ядер, расположенных вблизи долины стабильности, были установлены следующие закономерности:
Однако для ядер, удаленных от долины стабильности, ситуация иная. Для некоторых ядер, перегруженных нейтронами, наблюдается так называемый нейтронный слой - область вблизи поверхности ядра, в которой, с учетом фактора нормировки N/Zплотность нейтронов больше плотности протонов - ρn > ρp (см. рис. 4). В легких ядрах с большим отношением N/Z было открыто нейтронное гало. Нейтронное гало наблюдается в ядрах, у которых энергия связи нейтрона Bn < 1 - 1.5 МэВ. Оказалось, что в гало-ядрах наряду с кором, для которого плотности распределения протонов и нейтронов с точностью до фактора Z/A совпадают, существует довольно большая область периферии ядра, в которой плотность распределения нейтронов ρn существенно больше плотности распределения ρp протонов – ρn > ρp. Примерами ядер, имеющих нейтронное гало, являются изотопы 8He, 11Li, 14Be, 17B. Радиус нейтронного облака, окружающего кор ядра, оказывается существенно большим, чем радиус ядра, определяемый соотношением R ≈ 1.3 A1/3 Фм. Так для гало-ядра 11Li пространственное распределение двух нейтронов, образующих ядерное гало вокруг кора 9Li, простирается столь далеко, что радиус ядра 11Li оказывается сравним с радиусом ядра 208Pb (рис. 5).
Обнаружены также ядра, имеющие протонное гало – 9C, 17F, 17Ne. Наиболее подробную информацию о распределении электрических зарядов и токов в атомных ядрах получают в экспериментах по рассеянию на ядрах быстрых электронов. Данные о плотности распределения ядерной материи извлекаются из экспериментов по рассеянию на ядрах адронов. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

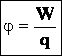

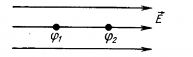


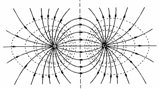
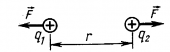
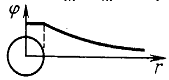
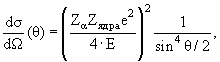
 Рис.
1. Распределение плотности ядерной
материи.
Рис.
1. Распределение плотности ядерной
материи.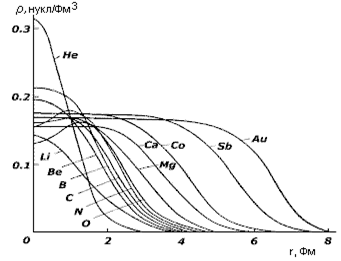 Рис. 2.
Плотность распределения ядерной
материи ядер, расположенных вблизи
долины стабильности.
Рис. 2.
Плотность распределения ядерной
материи ядер, расположенных вблизи
долины стабильности. Рис.
3. Радиусы атомных ядер, полученные
в экспериментах по рассеянию
электронов на ядрах.
Рис.
3. Радиусы атомных ядер, полученные
в экспериментах по рассеянию
электронов на ядрах. Рис.
4. Нейтронный слой ядра 22С:
ρn –
плотность пространственного
распределения нейтронов,
ρp –
плотность пространственного
распределения протонов.
Рис.
4. Нейтронный слой ядра 22С:
ρn –
плотность пространственного
распределения нейтронов,
ρp –
плотность пространственного
распределения протонов.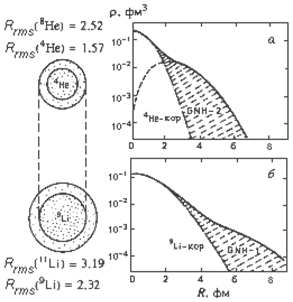 Рис.
5. Распределение нейтронной
плотности
в гало-ядрах 8He
и 11 Li.
Рис.
5. Распределение нейтронной
плотности
в гало-ядрах 8He
и 11 Li.