Содержание

Y

Введение 4

1. Расчет электрической цепи постоянного тока 5

1.1 Метод узловых и контурных уравнений 5

1.3Баланс мощностей 10

1.4 Потенциальная диаграмма 11

2. Расчет однофазной цепи переменного тока 13

2.1 Расчет символическим методом 13

3.1 Графоаналитический метод расчета 18

Литература 23

Нормативная документация 24

В ведение

Теоретические основы электротехники являются базовым общетехническим курсом для электротехнических и электроэнергетических специальностей вузов. Курс ТОЭ рассчитан на изучение в течение трех семестров и состоит из двух основных частей: теории цепей и теории электромагнитного поля. Данный лекционный курс посвящен первой из указанных частей ТОЭ -теории линейных и нелинейных электрических и магнитных цепей. Содержание курса и последовательность изложения материала в нем в целом соответствуют программе дисциплины ТОЭ для электротехнических и электроэнергетических специальностей вузов.

Цель данного курса состоит в том, чтобы дать студентам достаточно полное представление об электрических и магнитных цепях и их составных элементах, их математических описаниях, основных методах анализа и расчета этих цепей в статических и динамических режимах работы, т.е. в создании научной базы для последующего изучения различных специальных электротехнических дисциплин.

Задачи курса заключаются в освоении теории физических явлений, положенных в основу создания и функционирования различных электротехнических устройств, а также в привитии практических навыков использования методов анализа и расчета электрических и магнитных цепей для решения широкого круга задач.

В результате изучения курса студент должен знать основные методы анализа и расчета установившихся процессов в линейных и нелинейных цепях с сосредоточенными параметрами, в линейных цепях несинусоидального тока, в линейных цепях с распределенными параметрами, основные методы анализа и расчета переходных процессов в указанных цепях и уметь применять их на практике.

Знания и навыки, полученные при изучении данного курса, являются базой для освоения таких дисциплин, как: математические основы теории автоматического управления, теория автоматического управления, электропривод, промышленная электроника, электроснабжение промышленных предприятий, переходные процессы в электрических системах, электрические измерения и т. д.

П

Подпись

КР 27Г2к.09.00.00.000 ПЗ

ри изучении дисциплины предполагается, что студент имеет соответствующую математическую подготовку в области дифференциального и интегрального исчислений, линейной и нелинейной алгебры, комплексных чисел и тригонометрических функций, а также знаком с основными понятиями и законами электричества и магнетизма, рассматриваемыми в курсе физики.

1. Р асчет электрической цепи постоянного тока

• Метод узловых и контурных уравнений

• Метод контурных токов

• Баланс мощности

• Потенциальная диаграмма

1.1 Метод узловых и контурных уравнений

Для электрической цепи, изображенной на рисунке 1, выполнить следующее:

1. составить на основании законов Кирхгофа систему уравнений для определения токов во всех ветвях схемы;

2. определить токи во всех ветвях схемы, используя метод контурных токов;

3. составить баланс мощностей для заданной схемы;

4. результаты расчета токов по пунктам 2 и 3 представить в виде таблицы и сравнить;

5. построить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.

Рисунок 1 - Схемы электрической цепи постоянного тока

Таблица 1- Исходные данные

Дано	E1, B	E2, B	R1, Ом	R2, Ом	R3, Ом	R4, Ом	R5, Ом	R6, Ом
	50	30	53	34	24	18	25	42

1

Подпись

КР 27Г2к.01.00.00.000 ПЗ

)Составить систему уравнений, применяя законы Кирхгофа для определения токов во всех ветвях.

М етод узловых и контурных уравнений основан на применении первого и второго законов Кирхгофа. Он не требует никаких преобразований схемы и пригоден для расчета любой цепи.

При расчете данным методом произвольно задаем направление токов I₁, I₂, I₃, I₄, I₅, I₆в ветвях.

Составляем систему уравнений. В системе должно быть столько уравнений, сколько в цепи ветвей (неизвестных токов).

В заданной цепи шесть ветвей, значит, в системе должно быть шесть уравнений (m = 6). Сначала составляем уравнения для узлов по первому закону Кирхгофа. Для цепи с nузлами можно составить (n – 1) независимых уравнений.

В нашей цепи четыре узла (A, Б, С, Д), значит число уравнений: n

– 1 = 4 – 1 = 3.Составляем два уравнения для любых 3-х узлов, например, для узлов A, B, C.

узелA: I₁ – I₃− I₆ = 0

узелБ:I₂+ I₃ – I₄ = 0

узелВ: −I₁ + I₄–I₅ = 0

Всего в системе должно быть пять уравнений. Три уже есть. Три недостающих составляем для линейно независимых контуров. Чтобы они были независимыми, в каждый следующий контур надо включить хотя бы одну ветвь, не входящую в предыдущие.

Задаемся обходом каждого контура и составляем уравнения по второму закону Кирхгофа.

1. Контур ВГАВ – обход против часовой стрелки

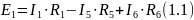
2. Контур ГБВГ – обход против часовой стрелки

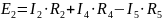
3. Контур ВАБВ – обход против часовой стрелки

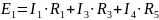
ЭДС в контуре берется со знаком “ + ”, если направление ЭДС совпадает с обходом контура, если не совпадает – знак “ – “.

Падение напряжения на сопротивлении контура берется со знаком “ + “, если направление тока в нем совпадает с обходом контура, со знаком “ – “, если не совпадает.

Мы получили систему из шести уравнений с шестью неизвестными:

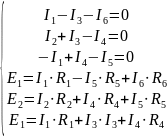
Подпись

КР 27Г2к.01.00.00.000 ПЗ

1 .2 Метод контурных токов

Метод контурных токов основан на использовании только второго закона Кирхгофа. Это позволяет уменьшить число уравнений в системе на n-1.

Достигается это разделением схемы на ячейки (независимые контуры) и введением для каждого контура-ячейки своего тока – контурного тока, являющегося расчетной величиной.

Итак, в заданной цепи на рисунке 1 можно рассмотреть три контура-ячейки (ВГАВ, ГБВГ, ВАБВ) и ввести для них контурные токи I_I, I_II, I_III.

Контуры-ячейки имеют ветвь, не входящую в другие контуры – это внешние ветви. В этих ветвях контурные токи являются действительными токами ветвей.

Ветви, принадлежащие двум смежным контурам, называются смежными ветвями. В них действительный ток равен алгебраической сумме контурных токов смежных контуров, с учетом их направления.

При составлении уравнений по второму закону Кирхгофа в левой части равенства алгебраически суммируются ЭДС источников, входящих в контур-ячейку, в правой части равенства алгебраически суммируются напряжения на сопротивлениях, входящих в этот контур, а также учитывается падение напряжения на сопротивлениях смежной ветви, определяемое по контурному току соседнего контура.

На основании вышеизложенного порядок расчета цепи методом контурных токов будет следующим:

стрелками указываем выбранные направления контурных токов I_k1, I_k2, I_k3в контурах-ячейках. Направление обхода контуров принимаем таким же;

составляем уравнения и решаем систему уравнений или методом подстановки, или с помощью определителей.

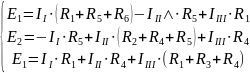
Подставляем в уравнение численные значения ЭДС и сопротивлений.

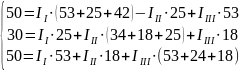
или

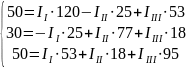
Решим систему с помощью определителей. Вычислим определитель системы Δ и частные определители Δ₁, Δ₂, Δ₃.

𝛥 =

Δ ₁ =

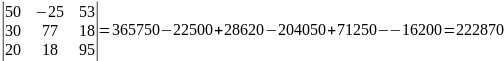
Δ₂ =

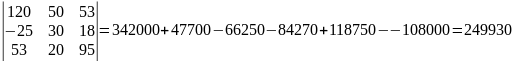
Δ₃ =

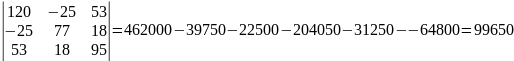
Вычисляем контурные токипо формуле:

(1.2)

где i – это номер контурного тока

Подставляем значения по формуле (1.2):

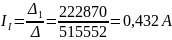
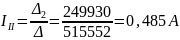
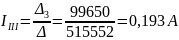
Действительные токи ветвей:

I₁ = I_I + I_III = 0,432 + 0,193 = 0,625A,

I₂ = I_II = 0,485 A,

I₃ = I_III = 0,193 A,

I₄ = I_II + I_III = 0,485 + 0,193 = 0,678A,

I₅ = I_II – I_I = 0,485 – 0,432 = 0,053 A,

I₆ = I_I = 0,432 A.

Подпись

КР 27Г2к.01.00.00.000 ПЗ