МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Государственное образовательное учреждение

высшего профессионального образования

Коми государственный педагогический институт

Кафедра алгебры, геометрии и

теории и методики обучения математике

Методические рекомендации

по подготовке к государственному

экзамену по математике

Сыктывкар, 2011

Составители: В.Ф.Бушуев, к.ф.-м.н., доцент;

Н.Г.Уляшова, к.ф.-м.н., доцент.

СОДЕРЖАНИЕ

ВОПРОС № 1 Определение группы. Свойства. Коммутативные (абелевы) группы. Конечные группы. Примеры групп. 3

ВОПРОС № 2 Определение кольца. Свойства. Коммутативные кольца. Делители нуля. Примеры колец. 9

ВОПРОС № 3 Определение поля. Свойства. Характеристика поля. Примеры полей. 12

ВОПРОС № 4 Определение векторного пространства. Свойства. Примеры векторных пространств. 16

ВОПРОС № 5 Конечномерные векторные пространства. Базис и размерность. Координаты вектора. 20

ВОПРОС № 6 Евклидовы пространства. Ортонормированные базисы. 25

ВОПРОС № 7 Простые и составные числа. Основная теорема арифметики о разложении чисел на простые множители и её применения. 29

ВОПРОС № 8 Приводимые и неприводимые многочлены. Теорема о разложении многочлена на неприводимые множители над произвольным полем. 33

ВОПРОС № 9 Разложение многочлена на неприводимые множители над полем комплексных и над полем действительных чисел. 37

ВОПРОС № 10 Корни многочлена. Отыскание целых и рациональных корней многочлена с целыми коэффициентами. 40

ВОПРОС № 11 Теорема о делении с остатком для целых чисел и для многочленов. 44

ВОПРОС № 12 Алгоритм Евклида для целых чисел и для многочленов. НОД и НОК. 49

ВОПРОС № 1 Определение группы. Свойства. Коммутативные (абелевы) группы. Конечные группы. Примеры групп.

Дадим определения понятий, на которых основано понятие группы, а именно понятие бинарной операции, нейтрального элемента относительно этой операции и элемента, симметричного данному элементу.

П.1. Бинарная операция.

Опр.1. Пусть А  произвольное непустое множество,  декартов квадрат множества А (т.е. множество всех пар элементов множества А). Бинарной операцией на множестве А называется отображение , которое каждой паре элементов множества А ставит в соответствие единственный элемент , обозначаемый .

Элемент с называют композицией элементов а и b (или результатом операции *, примененной к элементам а и b).

Часто используются аддитивная и мультипликативная форма записи бинарной операции.

При аддитивной форме записи бинарную операцию * называют сложением и обозначают +. При этом вместо пишут и элемент называют суммой элементов а и b.

При мультипликативной форме записи бинарную операцию * называют умножением и обозначают ∙. При этом вместо пишут и элемент называют произведением элементов а и b.

П.2. Виды бинарных операций.

Пусть *  бинарная операция на множестве А.

Опр.2. Операция * называется коммутативной, если .

Опр.3. Операция * называется ассоциативной, если .

Примеры:

1.  множество всех целых чисел. «+», «∙»  сложение и умножение целых чисел  коммутативны и ассоциативны.

2.  множество всех целых чисел. «»  бинарная операция вычитания на  не коммутативна и не ассоциативна. Действительно, ;

.

3. Пусть М  произвольное множество, а Р(М)  множество всех подмножеств множества М. Пересечение и объединение  это бинарные операции на множестве Р(М). Они коммутативны и ассоциативны.

П. 3. Нейтральные элементы

Опр.4. Пусть *  бинарная операция на множестве А. Элемент называют нейтральным относительно операции *, если .

При аддитивной форме записи бинарной операции нейтральный элемент обозначают символом 0 и называют нулевым элементом (или нулем).

При мультипликативной форме записи нейтральный элемент обозначают символом 1 или е и называют единичным элементом (или единицей).

Примеры:

1.  множество всех целых чисел. «+»  сложение целых чисел. 0  нейтральный элемент относительно сложения (нуль).

2.  множество всех целых чисел. «∙»  умножение целых чисел. 1  нейтральный элемент относительно умножения (единица).

3. Р(М), объединение .  нейтральный относительно элемент, т.к.

.

4. Р(М), пересечение . М  нейтральный относительно элемент, т.к.

.

Справедлива следующая теорема

Теорема.1. Пусть *  бинарная операция на множестве А. Если нейтральный относительно операции * элемент существует, то он единственный.

Доказательство: Допустим, что существует два нейтральных элемента  . Тогда по определению нейтрального элемента имеем

Раз для любого , то в частности,

▲.

П. 4. Симметричные элементы

Опр.5. Пусть *  бинарная операция на множестве А,  нейтральный относительно операции * элемент. Элемент называется симметричным к элементу относительно операции *, если .

При аддитивной форме записи операции симметричный к а элемент обозначается (а) и называется противоположным элементу а.

При мультипликативной форме записи симметричный к а элемент обозначается и называется обратным к элементу а.

Примеры:

1. Множество классов вычетов по модулю 6. «+»  операция сложения. Нейтральный относительно «+» элемент  , противоположный к классу относительно «+» элемент  класс . Действительно, . Значит  = .

2. , «∙»  операция умножения. Нейтральный относительно «∙» элемент  . . Действительно,

Справедлива следующая теорема

Теорема.2. Пусть *  бинарная операция на множестве А, *  ассоциативна и существует  нейтральный относительно этой операции * элемент.

Тогда: а) если существует симметричный к элементу элемент, то он единственный;

б) .

Доказательство: а) Допустим, что существует два симметричных к элементу а элемента  . Тогда .

б)

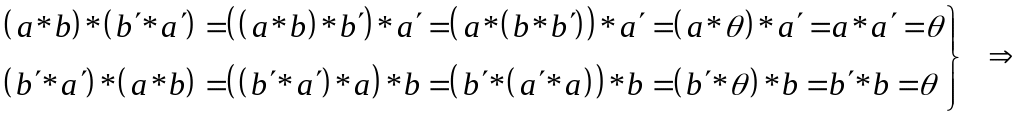
 симметричный к элементу элемент, т.е. . ▲