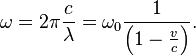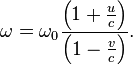Билет номер 10

1

Термодинамика – это наука о тепловых явлениях. В противоположность молекулярно-кинетической теории, которая делает выводы на основе представлений о молекулярном строении вещества, термодинамика исходит из наиболее общих закономерностей тепловых процессов и свойств макроскопических систем. Выводы термодинамики опираются на совокупность опытных фактов и не зависят от наших знаний о внутреннем устройстве вещества, хотя в целом ряде случаев термодинамика использует молекулярно-кинетические модели для иллюстрации своих выводов.

Термодинамика рассматривает изолированные системы тел, находящиеся в состоянии термодинамического равновесия. Это означает, что в таких системах прекратились все наблюдаемые макроскопические процессы. Важным свойством термодинамически равновесной системы является выравнивание температуры всех ее частей.

Если термодинамическая система была подвержена внешнему воздействию, то в конечном итоге она перейдет в другое равновесное состояние. Такой переход называется термодинамическим процессом. Если процесс протекает достаточно медленно (в пределе бесконечно медленно), то система в каждый момент времени оказывается близкой к равновесному состоянию. Процессы, состоящие из последовательности равновесных состояний, называются квазистатическими.

Одним из важнейших понятий термодинамики является внутренняя энергия тела. Все макроскопические тела обладают энергией, заключенной внутри самих тел. С точки зрения молекулярно-кинетической теории внутренняя энергия вещества складывается из кинетической энергии всех атомов и молекул и потенциальной энергии их взаимодействия друг с другом. В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении. Отсюда вытекает закон Джоуля, подтверждаемый многочисленными экспериментами.

Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема

Молекулярно-кинетическая теория приводит к следующему выражению для внутренней энергии одного моля идеального одноатомного газа (гелий, неон и др.), молекулы которого совершают только поступательное движение: 

Поскольку потенциальная энергия взаимодействия молекул зависит от расстояния между ними, в общем случае внутренняя энергия U тела зависит наряду с температурой T также и от объема V: 

U = U (T, V).

Таким образом, внутренняя энергия U тела однозначно определяется макроскопическими параметрами, характеризующими состояние тела. Она не зависит от того, каким путем было реализовано данное состояние. Принято говорить, что внутренняя энергия является функцией состояния.

Внутренняя энергия тела может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную). Например, если газ подвергается сжатию в цилиндре под поршнем, то внешние силы совершают над газом некоторую положительную работу A'. В то же время силы давления, действующие со стороны газа на поршень, совершают работу A = –A'. Если объем газа изменился на малую величинуΔV, то газ совершает работу pSΔx = pΔV, где p – давление газа, S – площадь поршня, Δx – его перемещение (рис. 3.8.1). При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна. В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой: 

Рисунок 3.8.1. Работа газа при расширении

Работа численно равна площади под графиком процесса на диаграмме (p, V). Величина работы зависит от того, каким путем совершался переход из начального состояния в конечное.

Внутренняя энергия тела может изменяться не только в результате совершаемой работы, но и вследствие теплообмена. При тепловом контакте тел внутренняя энергия одного из них может увеличиваться, а другого – уменьшаться. В этом случае говорят о тепловом потоке от одного тела к другому. Количеством теплоты Q, полученным телом, называют изменение внутренней энергии тела в результате теплообмена.

Передача энергии от одного тела другому в форме тепла может происходить только при наличии разности температур между ними.

Тепловой поток всегда направлен от горячего тела к холодному.

Количество теплоты Q является энергетической величиной. В СИ количество теплоты измеряется в единицах механической работы – джоулях (Дж).

Работа идеального газа

1. в изохорном процессе работа не совершается.  2. в изобарическом A=p(V2-V1).  3. в изотермическом A=m/M*RTln(V2/V1).  4. в адиабатном A=(p1V1/(x-1))(1-T2/T1), где х - показатель адиабаты.

2

       ЗАТУХАЮЩИЕ КОЛЕБАНИЯ - колебания с постоянно убывающей со временем амплитудой.

        Свободные колебания реальных систем всегда затухают. Затухание обусловлено в основном трением (механические системы) и сопротивлением ( в электромагнитных колебательных контурах).

        Колебательная система называется линейной, если её свойства не меняются при колебаниях, то есть такие параметры, как сила тяжести, упругость пружины, сопротивление, емкость, индуктивность не зависят ни от смещения, ни от скорости, ни от ускорения колеблющейся величины. В дальнейшем мы будем рассматривать только линейные системы.

   Чем меньше силы трения в системе, тем медленнее затухают колебания, тем лучше колебательная система.

Для характеристики качества колебательной системы вводится ряд параметров:

t = 1/b - время релаксации затухающих колебаний (за t  амплитуда уменьшается в e раз).   

Промежуток времени τ, за который амплитуда уменьшается в «е» раз, называется временем затухания (или релаксации), где «е» – основание натурального логарифма, е ≈ 2,718.

   - логарифмический декремент затухания; N - число колебаний, в течение которых амплитуда уменьшается в e раз. Соответственно, exp(bT) - просто декремент затухания.

   - добротность колебательной системы; W(t) - энергия (полная) колебательной системы в момент времени t.

Добротность Q колебательной системы – безразмерная физическая величина, равная произведению величины (2π) на отношение энергииW(t) системы в произвольный момент времени к убыли энергии за один период затухающих колебаний:

3.          

Билет номер 11

1(1)

Звуковые волны

Под звуком понимают упругие волны среды, воспринимаемые ухом человека. Опыт показывает, что наше ухо воспринимает как звук механические колебания, частота которых лежит в пределах от 20 Гц до 20 кГц. Упругие волны с частотой менее 20 Гц называются инфразвуком, с частотой более 20 кГц - ультразвуком.

Звук может распространяться в виде продольных и поперечных волн. В газообразной и жидкой фазе возникают только продольные волны, в твердых телах, помимо продольных, возникают также и поперечные волны.

В зависимости от структуры спектра колебания среды различают шумы и музыкальные звуки. Шумы - это непериодические колебания. Им соответствует сплошной спектр, т. е. набор частот, непрерывно заполняющих некоторый интервал. Музыкальные звуки обладают линейчатым спектром с кратными частотами, следовательно, они представляют собой периодические колебания.

Для слушающего человека сразу становятся очевидными две характеристики звука, а именно его громкость и высота тона. Каждой из этих субъективных характеристик соответствует величина, измеряемая физическими методами. Громкость связана с энергией звуковой волны, которая представляет продольные колебания воздуха. Согласно уравнению (4.8) энергия волны пропорциональна квадрату амплитуды.

Человеческое ухо способно воспринимать звуки с интенсивностью вплоть до 10^-12 Вт/м² (порог слышимости) и до 1 Вт/м² (так называемый порог болевого ощущения). Громкость зависит также от частоты звука. Поэтому величина, которую мы воспринимаем, как громкость, не прямо пропорциональна интенсивности. Но, чем больше интенсивность, тем звук громче. Высота тона звука определяется частотой упругих колебаний, воспринимаемых ухом.

Звук характеризуется тембром. Тембр звука, или иногда называют его окраской звука, определяется амплитудами и частотой дополнительных обертонов (звуки более высокой частоты). На основной тон могут накладываться обертоны с различными амплитудами, что и определяет тембр звука.

1(2)

Эффе́кт До́плера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника. Эффект назван в честь австрийского физика К. Доплера.

Сущность явления[

Эффект Доплера легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной. Предположим, сирена выдаёт какой-то определённый тон, и он не меняется. Когда машина не движется относительно наблюдателя, тогда он слышит именно тот тон, который издаёт сирена. Но если машина будет приближаться к наблюдателю, то частота звуковых волн увеличится, и наблюдатель услышит более высокий тон, чем на самом деле издаёт сирена. В тот момент, когда машина будет проезжать мимо наблюдателя, он услышит тот самый тон, который на самом деле издаёт сирена. А когда машина проедет дальше и будет уже отдаляться, а не приближаться, то наблюдатель услышит более низкий тон, вследствие меньшей частоты звуковых волн.

Для волн (например, звука), распространяющихся в какой-либо среде, нужно принимать во внимание движение как источника, так и приёмника волн относительно этой среды. Дляэлектромагнитных волн (например, света), для распространения которых не нужна никакая среда, в вакууме имеет значение только относительное движение источника и приёмника^[1].

Эффект был впервые описан Кристианом Доплером в 1842 году.

Также важен случай, когда в среде движется заряженная частица с релятивистской скоростью. В этом случае в лабораторной системе регистрируется черенковское излучение, имеющее непосредственное отношение к эффекту Доплера.

Математическое описание

Если источник волн движется относительно среды, то расстояние между гребнями волн (длина волны λ) зависит от скорости и направления движения. Если источник движется по направлению к приёмнику, то есть догоняет испускаемую им волну, то длина волны уменьшается, если удаляется — длина волны увеличивается:

где   — круговая частота, с которой источник испускает волны,   — скорость распространения волн в среде,   — скорость источника волн относительно среды (положительная, если источник приближается к приёмнику и отрицательная, если удаляется).

Частота, регистрируемая неподвижным приёмником

Аналогично, если приёмник движется навстречу волнам, он регистрирует их гребни чаще и наоборот. Для неподвижного источника и движущегося приёмника

где   — скорость приёмника относительно среды (положительная, если он движется по направлению к источнику).

Подставив вместо   в формуле (2) значение частоты   из формулы (1), получим формулу для общего случая:

2(1)

Вприроде существует несколько типов полей: гравитационное, электромагнитное, сильное, слабое. Каждое имеет свою константу взаимодействия или заряд (так, например, массу m можно назвать гравитационным зарядом). Вокруг тел, имеющих электрический заряд, всегда существует электрическое поле. Вначале мы рассмотрим свойствапокоящихся зарядов, между которыми действуют только электрические силы. Электрическое поле, созданное системой покоящихся зарядов, называетсяэлектростатическим полем.

Точечным зарядом является заряженное тело, геометрическими размерами которого в данных условиях можно пренебречь. Закон Кулона (1785 г.) устанавливает, что сила Кулона или сила взаимодействия двух точечных электрических зарядов   и  , находящихся в вакууме на расстоянии   друг от друга, определяется выражением  , где  - это единичный радиус-вектор, направленный вдоль линии, соединяющей точечные заряды, 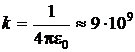 м/Ф, а постоянная  Ф/м называется электрической постоянной.

Величину электрического поля можно определить по величине кулоновской силы  , с которой поле действует на пробный заряд  . Но само поле заряда   не должно зависеть от величины  . Поэтому электрическое поле принято характеризовать вектором напряженности   .

Электрическое поле изображается с помощью силовых линий - это линии, касательные к которым в каждой точке совпадают с направлением вектора напряженности   (не имеющий начальной скорости свободный точечный заряд   в электрическом поле всегда начинает двигаться вдоль силовой линии). Плотность силовых линий или число силовых линий  , пересекающих расположенную под прямым углом площадку  , пропорционально величине напряженности поля   в данной точке. Силовые линии электрического поля начинаются на положительных зарядах и заканчиваются на отрицательных, либо уходят в бесконечность. Теорема Гаусса для электрического поля: поток вектора напряженности электростатического поля через любую замкнутую поверхность равен алгебраической  сумме заключенных внутри этой поверхности зарядов, деленной на  : , или (теорема Остроградского-Гаусса для электростатического поля в дифференциальной форме).

Электростатическое поле потенциально и характеризуется потенциалом. , т.е. потенциал равен потенциальной энергии единичного точечного заряда в данной точке поля. При решении электростатических задач полезно учитывать и следующее утверждение: точечный заряд  в точке с потенциалом   всегда обладает потенциальной энергией  , поэтому работа по перемещению точечного заряда   в любом электростатическом поле всегда равна произведению величины заряда на разность потенциалов между точками начального и конечного положений заряда:  Совокупность точек (поверхность) с одинаковым потенциалом называетсяэквипотенциальной поверхностью. Вектор напряженности связан с потенциалом соотношением  ,

и силовые линии поля всегда перпендикулярны к эквипотенциальным поверхностям.

Для электростатического поля циркуляция вектора напряженности по любому замкнутому контуру равна нулю:  - это теорема о циркуляции вектора  Следовательно, электростатическое поле – потенциальное поле.