Симметричные составляющие несимметричных трехфазных систем.
Цель работы:
Ознакомиться практически с разложением несимметричных систем ЭДС на симметричные трехфазные системы.
Исследовать возможности возникновения несимметричных систем в трехфазных цепях.
Краткая теория
Несимметрия в трехфазной цепи может быть вызвана различными причинами.:
Неодинаковым сопротивлением фаз (несимметричная нагрузка).
Несимметрчным коротким замыканием ( например, между двумя фазами или фазой и нейтральным проводом);
Размыканием фазы;
Неравенством ЭДС и т.п.
Для расчета несимметричных режимов трехфазных электрических цепей в общем случае применяется метод симметричных составляющих, основанный на представлении любой трехфазной несимметричной системе электрических величин (токов, напряжений ) в виде суммы трех симметричных систем. Эти симметричные системы величин , образующих в совокупности несимметричную систему, носят название симметричных составляющих прямой, обратной и нулевой последовательностей (рис.9). При этом под последовательностью подразумевается порядок следования во времени максимумов фазных величин. Симметричные составляющие обозначаются цифрами 1,2,0.
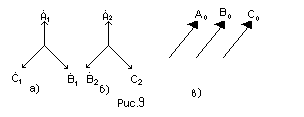
Векторами, показанными на рис.9 могут изображаться как комплексные амплитуды, так и комплексные действующие значения токов трех последовательностей.
Взаимное расположение и модуль векторов прямой, обратной и нулевой последовательностей зависят от характера несимметрии и электрических параметров трехфазной цепи.
На основании рис.9 :
;
;
;
;
(1)
где
- фазовый оператор.
С учетом этих выражений токи в фазах А, В и С определяются как суммы соответствующих симметричных составляющих :
;
;
.
(2)
С учетом выражений (1) и при пренебрежении индексами получим :
;
;
.
(3)
Эти формулы служат для нахождения фазных токов по их симметричным составляющим.
Если известны фазные токи, то могут быть найдены симметричные составляющие :
(4)
Аналогичные выражения могут быть записаны и для фазных напряжений.
Линейное напряжение не содержит составляющей нулевой последовательности.
В
цепи с нулевым проводом ток в нулевом
проводе равен геометрической сумме
фазных токов:
Следовательно,
составляющая нулевой последовательности
равна одной трети тока в нулевом проводе:
.
В цепи без нулевого провода линейные токи не имеют составляющей нулевой последовательности.
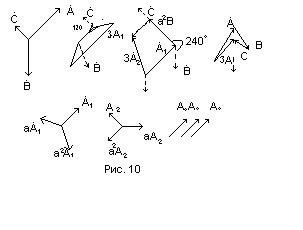
Симметричные составляющие несимметричных токов и напряжений могут быть определены также графическим путем.
На рис. 10 а, б, в представлены графическим путем нулевая, прямая и обратная последовательности.
Порядок выполнения работы
Собрать электрическую цепь по схеме рис. 11.
П
ри
питании цепи симметричной системой
напряжений измерить все токи и напряжения
при симметричной и несимметричной
нагрузке как с нулевым проводом, так и
без него.Произвести те же измерения при питании цепи несимметричной системой напряжений, когда нагрузка симметричная и несимметричная как с нулевым проводом, так и без него.
Прямая Обратная Нулевая
последовательность последовательность последовательность
Рис. 11