2

Федеральное агентство по образованию

Государственное образовательное учреждение высшего

профессионального образования

«Восточно-Сибирский государственный технологический университет»

(ГОУ ВПО ВСГТУ)

Теоретическая электротехника основы теории цепей

Методические указания по проведению практических занятий

для студентов всех специальностей электротехнических и

радиотехнических направлений очной формы обучения.

Составитель: Федоров К.А.

Издательство ВСГТУ

Улан-Удэ 2009г

Настоящее учебное пособие предназначено для преподавателей и студентов, оно содержит методические и справочные материалы для проведения практических занятий по курсам «Основы теории цепей» и «Теоретические основы электротехники». Пособие может быть использовано студентами всех специальностей электротехнических и радиотехнических направлений очного и заочного обучения, изучающими указанные курсы, при решении контрольных задач, а также при выполнении контрольных и расчетно-графических работ. Пособие содержит необходимые теоретические сведения и примеры решения конкретных типовых задач по основным разделам данных курсов.

СОДЕРЖАНИЕ

Стр.111

Предисловие ……………………………………………………….. 2

Тема 1. Линейные электрические цепи постоянного тока …....... 5

Тема 2. Однофазные электрические цепи синусоидального

тока …………………………………………………........................ 12

Тема З. Трёхфазные цепи ………………………………………… 19

Тема 4. Несинусоидальные периодические токи и

напряжения …………………………………………………………. 23

Тема 5. Четырёхполюсники …………………………………… … 25

Тема 6. Переходные процессы в линейных электрических

цепях ……………………………………………………………….. 27

Библиографический список …………………………………………. 36

Тема 1. Линейные электрические цепи постоянного тока.

Порядок решения задач рассматривается на примере цепи, изображенной

на рис.1., в которой Е₁ = 70 В, Е₂=40 В, Е₅ = 25 В, Е₆ = 35 В; J₃=1А;

R₁ = 6 Ом, R₂ = 20 Ом, R₃ = 20 Ом, R₄ = 10 Ом, R₅ = 15 Ом, R₆ = 5 Ом.

Рис.1. Исходная цепь

ЗАДАЧА 1. Составление уравнений на основании законов Кирхгофа.

Решение начинают с выбора условно-положительных направлений токов во всех ветвях цепи. При записи уравнений необходимо помнить, что ветви с источниками тока в расчетные контуры не входят:

а) I₁ + I₄ – I₆ = 0;

в) - I₁ + I₂ – I₃ = 0;

с) - I₂ – I₄ – I₅ = 0;

A) I₁R₁ + I₂R₂ – I₄R₄ = E₁;

B) - I₂R₂ + I₃'R₃ + I₅R₅= E₅ – E₂;

C) I₄R₄ – I₅R₅ + I₆R₆ = E₆ – E₅.

В уравнении для контура В записано произведение I₃^’R₃, так как именно ток I₃^’ протекает по резистору R₃.

ЗАДАЧА 2. Расчет линейной цепи постоянного тока методом контурных токов. 11Вначале желательно преобразовать все источники тока в эквивалентные источники напряжения и начертить схему полученной электрической цепи (рис. 2). Эквивалентная ЭДС определяется как Е₃ = J₃R₃, отсюда

Е₃ = 1∙20 = 20 В.

Составляем уравнения контурных токов:

A) I_A(R₁ + R₂ + R₄) – I_BR₂ – I_CR₄= E₁ + Е₂;

B) - I_AR₂ + I_B(R₂ + R₃ + R₅) – I_CR₅ = -E₁ – E₃ + E₅;

C) - I_AR₄ – I_BR₅ + I_C(R₄ + R₅ + R₆) = E₆ – E₅ .

Подставляя числовые данные в приведенные уравнения и решая их, получим

I_А = 5 А; I_В = 2 А; I_С = 3 А.

Реальные токи в исходной цепи определяют по контурным токам, причем ветви с источниками тока составляют контур, в котором контурный ток равен задающему току этого источника тока:

I₁=I_A = 5 A; I₂ = I_A- I_B = 5-2 = 3 A; I₃ = -I_B = -2 A; I₃' = I_B + J₃ = 2+3 = 5 А; I₄ = I_C - I_A = 3-5=2 A; I₅=I_B-I_c = 2-3=-1 A; I₆ = -I_C = -3 A.

Знак минус у токов I₃, I₄, I₅, I₆ показывает, что их истинные направления противоположны направлениям, принятым на рис.1, но эти направления следует оставить.

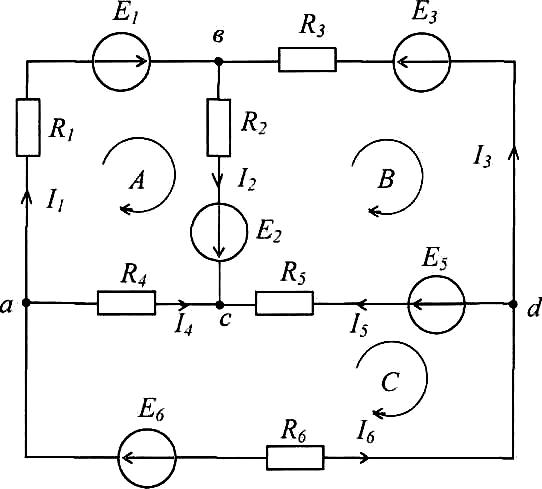
Рис.2. Цепь для расчета методом контурных токов

ЗАДАЧА 3. Расчет линейной цепи постоянного тока методом узловых потенциалов.

Перед составлением уравнений желательно преобразовать все источники напряжения в эквивалентные источники тока и выбрать узел цепи, потенциал которого можно приравнять нулю, пусть это будет узел d, Ф_d = 0 (рис. 3):

где i - номер ветви с исходным источником напряжения.

Составляем уравнения узловых потенциалов для узлов а, в, с:

Подставляя числовые данные в записанные уравнения и решая их, получим

Ф_а = 20 В; Ф_в = 60 В; Ф_с = 40 В.

Реальные токи в исходной цепи определяют по обобщенному закону Ома, например,

Здесь в круглых скобках записан потенциал верхнего (по схеме рис. 3) вывода резистора Аналогично можно найти и остальные токи.

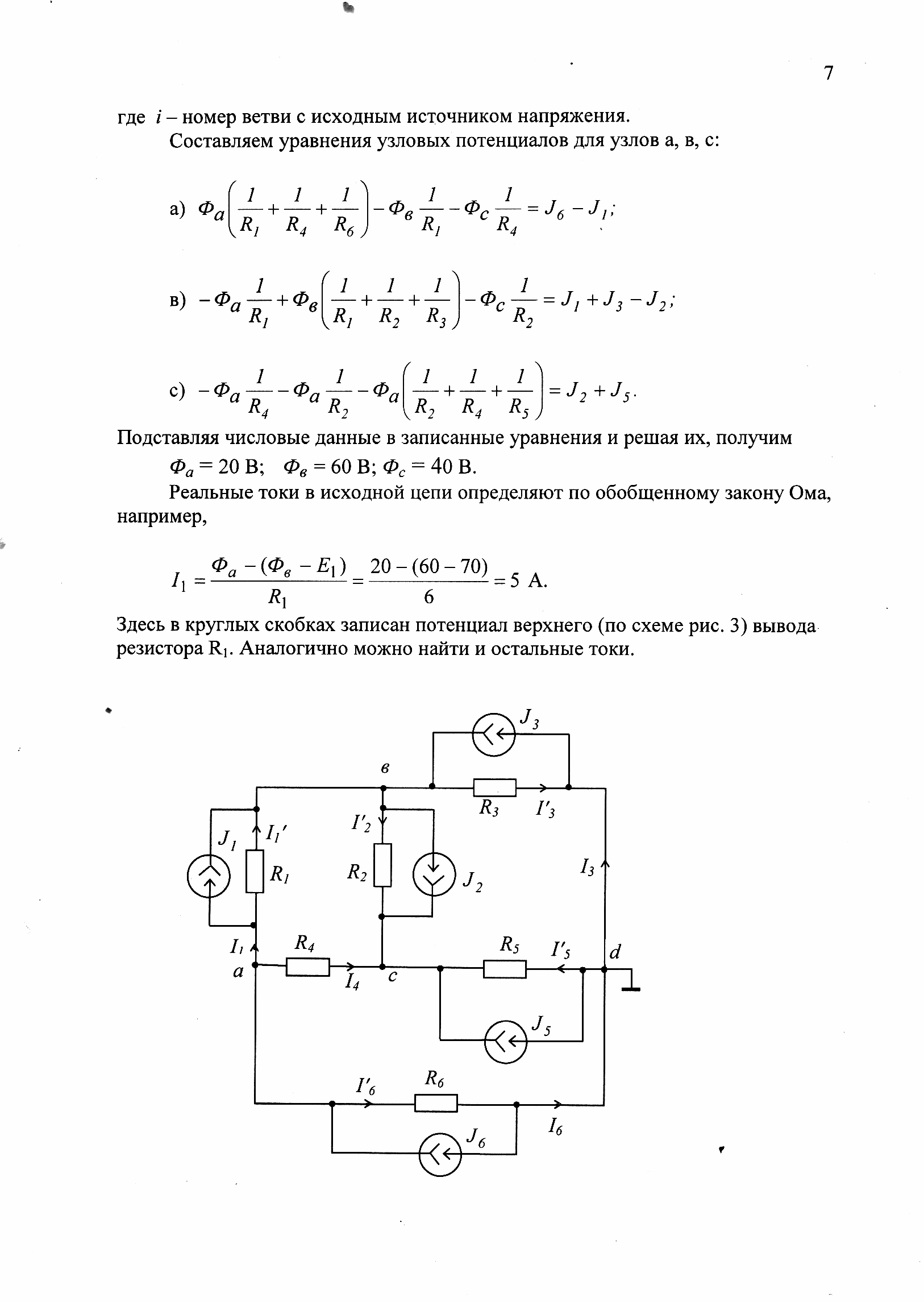
Рис. 3. Цепь для расчета методом узловых потенциалов

ЗАДАЧА 4. Расчет баланса мощностей линейной цепи постоянного тока.

Мощность источника (напряжения или тока) записывают со знаком плюс, если ток, протекающий через источник, противоположен по направлению напряжению на зажимах источника, в противном случае мощность источника отрицательна. Для источника напряжения можно сравнить направления тока через источник и ЭДС источника: если они совпадают, то мощность источника положительна, в противном случае мощность источника записывают со знаком минус. Для данной цепи мощность источников равна

P_ист=E₁I₁ + E₂I­₂ + J₃U_вd + E₅I₅ – E₆I₆.

Здесь мощность источника тока J₃ можно найти несколькими способами:

P_из=J₃U_вd= - J₃U_dв= - J₃(Ф_d – Ф_в)=J₃(I`₃R₃).

Подставляя числовые значения величин (с учетом их знаков), получим:

P_ист=70∙5 + 40∙3 + 1∙ (3∙20) + 25∙ (-1) – 35∙ (-3) = 610 Вт.

Мощность приемников всегда положительна:

P_пр=I_I² R₁ + I₂² R₂ + I₃^`2 R₁ + I₄² R₄ + I₅² R₅ + I₆² R₆.

Здесь в третьем слагаемом правой части уравнения записан ток I₃^`, так как именно он протекает по резистору R₃. Подставляя числовые значения величин, можно получить

Р_пр= 610 Вт,

т.е. баланс сходится. При Р_ист ≠P_пр баланс считается выполненным, если расхождение между Р_ист и Р_пр не более 3 %. Обозначая большую из этих мощностей Р_Б, а меньшую Р_М, имеем условие выполнения баланса:

ЗАДАЧА 5. Расчет линейной цепи постоянного тока методом активного двухполюсника (эквивалентного генератора).

Найдем ток второй ветви. Применяя любой метод расчета электрических цепей, определим напряжение холостого хода (рис. 4). Пусть это будет метод контурных токов. Поменяем местами ветви Е₆ – R₆ и R₄ - R₅ - Е₅ (рис. 5).

Составим уравнения:

I_1x(R₁ +R₃ + R₆) – U_4xR₆ = E₁ - E₃ + E₆;

-I_1xR₆ + I_4x(R₆ + R₄ +R₅) =E₅- E₆.

Рис. 4. Цепь для расчета напряжения холостого хода

Рис. 5. Преобразованная цепь для расчета

Подставляя числовые данные и решая систему уравнений, имеем:

I_1x = 2,762 А; I_4х = 0,127 А.

Для определения U_x запишем уравнение второго закона Кирхгофа для любого контура, включающего искомое напряжение, например для контура

R₁ – Е₁ - U_x - Е₂ – R₄ – R₁:

I_1xR_I + U_x+I_4xR₄ = E₁+ E₂ .

Отсюда U_X = E₁+E₂- I_1xR₁ - I_4xR₄ = 70 + 40 - 2,762∙6 - 0,127∙10 =92,158 В.

Для вычисления входного сопротивления R_вx составляют схему пассивной части активного двухполюсника (рис. 6), в которой идеальные источники напряжения закорачиваются, а идеальные источники тока размыкаются.

Рис. 6. Цепь для расчета входного сопротивления

Преобразуем треугольник сопротивлений R₁ - R₃ – R₆ между точками а, в, d в эквивалентную звезду (рис. 7).

Рис. 7. Преобразованная цепь для расчета

Сопротивления звезды R_a , R_в, R_d равны

11111

Для цепи рис. 7 получим:

Искомый ток

ЗАДАЧА 6. Расчет и построение потенциальной диаграммы линейной цепи постоянного тока.

Для построения потенциальной диаграммы выбираем контур С исходной цепи и вводим обозначения точек после каждого элемента контура (добавлены точки е и f (рис.8)).

Рис. 8. К расчету потенциальной диаграммы

Примем потенциал точки d за нуль и определим потенциалы остальных точек контура (направление обхода - по движению часовой стрелки):

Ф_d = 0;

Ф_f = Ф_d + I₆R₆ = 0 + (-3)∙5 = -15 В;

Ф_a = Ф_f + E₆ = -15 + 35 = 20 B;

Ф_с = Ф_a – I₄R₄ = 20 – (-2) ∙10 = 40 B;

Ф_e = Ф_с + I₅R₅ = 40 + (-1) ∙15 = 25 B;

Ф_d = Ф_e – E₅ = 25 – 25 = 0. 11Потенциальная диаграмма построена на рис. 9. По оси абсцисс откладывается сумма сопротивлений контура. Вертикальные отрезки af и ed численно равны в масштабе ЭДС Е₆ и Е₅ соответственно.

Рис. 9. Потенциальная диаграмма.