2. Питання до теми

1. За якої умови використовується формула Пуассона7

2. Записати формулу Пуассона для малоймовірних випадкових подій.

3. Записати асимптотичні формули для обчислення ймовірностей випадкових подій для n незалежних експериментів за схемою Бернуллі.

4. Чому дорівнює ?

5. Чому дорівнює ?

6. Чому дорівнює ?

5. Сформулювати локальну теорему Муавра – Лапласа.

7. Сформулювати інтегральну теорему Муавра – Лапласа.

3. Розв’язання завдань

Приклад 1. Фабрика випускає 75% виробів 1-го сорту. Із партії готових виробів навмання беруть 400 деталей. Обчислити ймовірність таких випадкових подій:

1) виробів 1-го сорту виявиться 290 шт.;

2) 300 шт.;

3) 320 шт.

Розв’язання. За умовою задачі маємо:

n=400; p = 0.75; q = 0.25; m = 290; 300; 320.

1)

;

;

3)

Приклад 2. Імовірність того, що посіяне зерно проросте в лабораторних умовах, у середньому дорівнює 0,9. Було посіяно 700 зернин ячменю в лабораторних умовах. Визначити найімовірніше число зернин, що проростуть із цієї кількості зернин, та обчислити ймовірність цього числа.

Розв’язання. За умовою задачі маємо:

n=700; p = 0.9; q = 0.1.

Отже, шукане число дорівнює 630.

Відповідна ймовірність буде така:

Приклад 3. Верстат-автомат виготовляє однотипні деталі. Імовірність того, що виготовлена одна деталь виявиться стандартною, є величиною сталою і дорівнює 0,95. За зміну верстатом було виготовлено 800 деталей. Яка ймовірність того, що стандартних деталей серед них буде:

1) від 720 до 780 шт.;

2) від 740 до 790 шт.

Розв’язання. За умовою задачі маємо:

n=800; p = 0.95; q = 0.05; 720 m 780; 740 m 790.

1)

2)

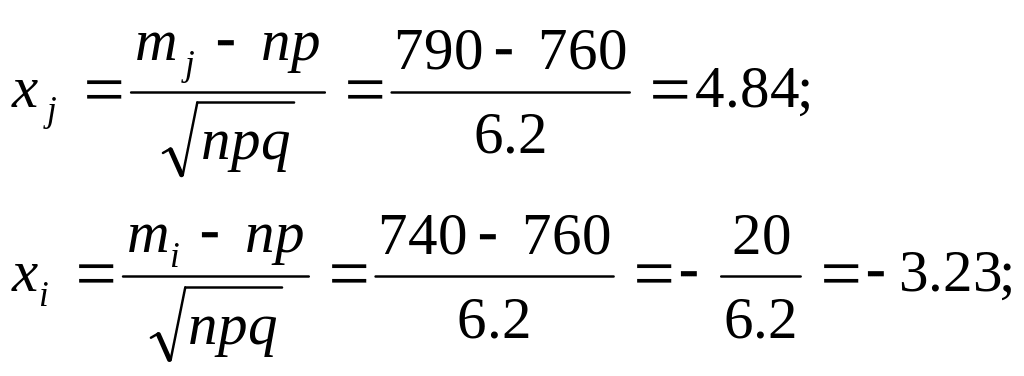
Приклад 4. В електромережу ввімкнено незалежно одну від одної 500 електролампочок, які освітлюють у вечірній час виробничий цех заводу. Імовірність того, що електролампочка в електромережі не перегорить, є величиною сталою і дорівнює 0,8. Яка ймовірність того, що з 500 лампочок не перегорить не більш як 380 шт.?

Розв’язання. За умовою задачі маємо:

n=500; p = 0.8; q = 0.2; 0 m 380

Приклад 5. Радіоприлад містить 1000 мікроелементів, які працюють незалежно один від одного, причому кожний може вийти з ладу під час роботи приладу з ймовірністю р = 0,002. Обчислити ймовірності таких випадкових подій:

1) під час роботи приладу з ладу вийдуть 3 мікроелементи;

2) від трьох до шести.

Розв’язання. За умовою задачі маємо: р = 0,002; ; n =1000; m =3, . Оскільки n велике, а р мале число, то для обчислення ймовірностей застосуємо формули (13) та (14). Для цього обчислимо значення параметра а=np=1000*0,002=2.

1)

2) =

Приклад 6. Імовірність появи випадкової події в кожному з 900 незалежних експериментів є величиною сталою і дорівнює 0,75. Яким має бути значення , щоб 0,99?

Розв’язання. За умовою задачі р = 0,75; q =0,25; n =900; 2Ф(х) = 0,99. Далі маємо Ф(х) = 0,495; х =2,74 і

Отже, умову задачі задовольняє значення .