Міністерство освіти і науки України

Відокремлений структурний підрозділ Національного авіаційного університету Слов’янський коледж Національного авіаційного університету

Теорія ймовірностей

ТА

Математична статистика Методичні вказівки до практичних занять

Для спеціальностей 6.030509 «Облік і аудит»

6.030507 «Маркетинг»

СЛОВ'ЯНСЬК

2010

Тема: Розв’язування задач з використанням формул комбінаторики.

1. Теоретичні вказівки

Імовірністю випадкової події називається відношення кількості подій, які сприяють цій події, до кількості всіх рівноможливих несумісних подій, які утворюють повну групу подій під час певного випробування.

, де - загальна кількість рівноможливих і несумісних подій, які утворюють повну групу, - число елементарних подій, які сприяють події А.

Якщо А – випадкова подія, тобто така, що може відбутися або не відбутися, то імовірність її задовольняє нерівність

2. Питання до теми

1. Яка подія називається вірогідною? Навести приклади.

2. Яка подія називається елементарною; складеною випадковою подією? Навести приклади.

3. Що називається простором елементарних подій? Навести приклади.

4. Сумою двох випадкових подій А і В називається ...

5. Добутком двох випадкових подій А і В називається ...

6. Дати класичне означення ймовірності випадкової події.

3. Розв’язання завдань

1. Маємо 10 лотерейних білетів. На кожний із них може випасти виграш із певною ймовірністю.

Побудувати простір елементарних подій (множину ) числа білетів, на які випаде виграш, а також такі випадкові події:

А – із 10 білетів виграють не більше як три;

В – із 10 білетів виграють не менш як п’ять.

Обчислити Р(А), Р(В), Р(А В).

Р(А В)=0.

2. Задано дві множини цілих чисел: ₁= , ₂= . Із кожної множини навмання беруть по одному числу. Побудувати простір елементарних подій для цього експерименту і такі випадкові події:

А – сума цифр буде кратною 3;

В – сума цифр буде кратною 7.

Обчислити Р(А), Р(В), Р(А В).

, , Р(А В)=0.

3. Гральний кубик підкидається один раз, а монета чотири рази. Побудувати простір таких елементарних подій – поява числа на гральному кубику і поява герба на монеті, а також випадкові події:

А – на гральному кубику з’явиться число, кратне 2, і герб при цьому випаде не менш як двічі;

В – на гральному кубику з’явиться число, кратне 3, і герб при цьому випаде не більш як тричі.

Обчислити Р(А), Р(В), Р(А В).

, , Р(А В)=

4. В електромережу ввімкнено 15 електролампочок. Кожна з яких може перегоріти із певною ймовірністю. Визначити простір елементарних подій (множину ) – числа електролампочок, що не вийдуть із ладу, і такі випадкові події:

А – число електролампочок, що не вийдуть із ладу, буде не більшим від чотирьох;

В – від трьох до шести.

Обчислити Р(А), Р(В), Р(А В).

, , Р(А В)=

5. Монета підкидається 20 раз. Яка ймовірність того, що при цьому герб з’явиться 7 або 17 раз?

А - герб з’явиться 7 або 17 раз.

Обчислити Р(А).

Р(А) = .

6. На кожній із п’яти однакових карток написана одна із цифр 1,2,3,4,5. Навмання картки розкладають в один рядок. Обчислити ймовірність таких випадкових подій:

А – цифри на картках утворюють зростаючу послідовність;

В – спадну послідовність;

С – цифри 1,2 розміщуватимуться в такій послідовності на початку рядка;

D – цифра 1 стоятимемо на першому місці, а 5 – на останньому.

, Р(В) = , Р(С) = ,

7. Задано множину цілих чисел = . Числа навмання розміщуються в рядок. Яка ймовірність того, що при цьому утвориться парне п’ятицифрове число?

8. Маємо тринадцять однакових карток з буквами Е, Е, А,А, Е, І, П, Л, Л, Д, Р, П, П, які навмання розкладають у рядок. Яка ймовірність того, що при цьому дістанемо слово „паралелепіпед”.

9. Дев’ять пасажирів навмання розміщуються у трьох вагонах. Обчислити ймовірність таких випадкових подій:

А – у кожному вагоні виявиться по три пасажири,

В – у першому вагоні виявиться 4 пасажири, у другому – 3 і в третьому – 2 пасажири.

,

=

10. В урні міститься 4 червоних, 5 синіх і 6 зелених кульок. Навмання із урни беруть три кульки. Яка ймовірність того, що вони виявляться одного кольору або всі три будуть мати різні кольори?

11. В урні міститься 20 кульок, пронумерованих відповідно від 1 до 20. Кульки з урни виймають по одній із поверненням. Таким способом кульки виймалися 10 разів. Яка ймовірність того, що номери кульок утворять зростаючу послідовність?

12. Підкидається n штук гральних кубиків. Обчислити ймовірність таких випадкових подій:

А – сума випадкових цифр дорівнюватиме n;

В – сума цифр, що випали, дорівнюватиме n+1.

Р(А) =

Р(В) =

13. У бригаді робітників 5 чоловіків і 10 жінок. Яка ймовірність того, що навмання розбиваючи їх на 5 груп по три чоловіки, у кожній із них виявиться один чоловік.

15 робітників можна розбити на 5 трійок так:

;

10 жінок можна розбити на 5 груп, по дві жінки в кожній групі так:

;

5 чоловіків можна розмістити в 5 групах 5! способами. Отже,

.
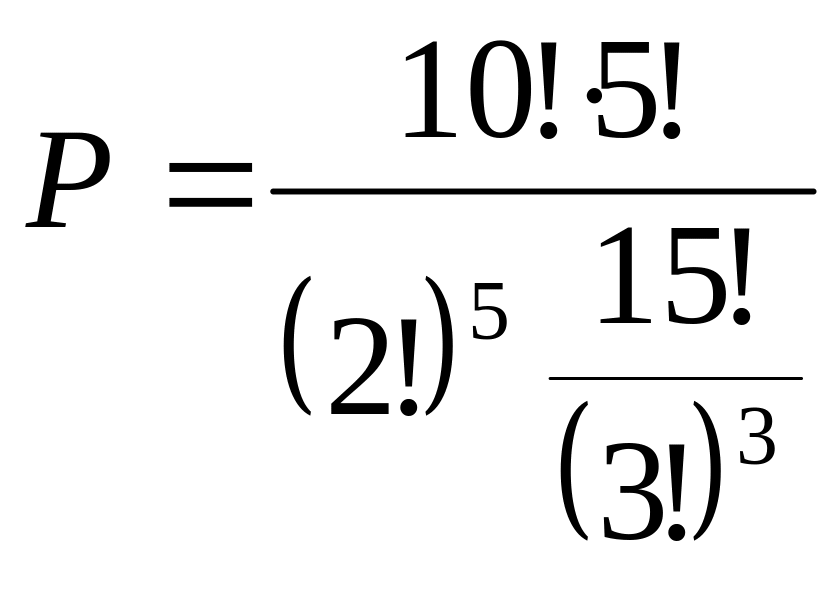