Смешивание

Смешивание цветов это процесс, который контролируется лишь внутренним устройством человека. Поэтому существуют различные формулы смешивания, каждая из которых, вообще говоря, не совсем верна с точки зрения человеческого восприятия.

Обозначим операцию смешивания, как  и рассмотрим некоторые варианты смешивания в пространстве RGB.

Среднее

Наиболее популярной формулой является среднее.

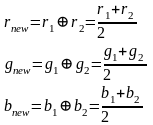
Т.к суммирование выполняется по каналам, то можно рассматривать только 1 сумму.

(R₁R₂) R₃=R₁/4+R₂/4+R_3­/2

R₁ (R₂R₃)=R₁/2+R₂/4+R_3­/4

Легко заметить, что операция является коммутативной и не является ассоциативной.

И задача нахождения второго цвета участвующего в суммировании имеет не более одного решения, для заданного результата и одного цвета. Причём если решение существует, оно находиться крайне быстро.

Легко находиться условие существования решения уравнения R₁x= R₂:

0≤ 2R₂-R₁ ≤255

Недостатки формулы:

Из принципа RGB мы знаем, что желтый=красный+зеленый. А по нашей формуле красный+зеленый даёт не желтый.

Рисунок 8. Смесь красного и зеленого не даёт желтый

Сложение по модулю 256

Т.к среднее имеет некоторые недостатки, можно рассмотреть вариант сложения значений интенсивности по каналам. И брать значение по модулю 256 для обеспечения нахождения результата в пространстве RGB

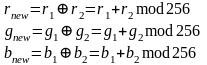
Данная формула обладает свойством ассоциативности и коммутативности.

Существует нейтральный элемент = 0(черный цвет).

Задача нахождения второго цвета участвующего в суммировании всегда имеет единственное решение, для заданного результата и одного цвета. Причём, оно находиться крайне быстро.

Однако результат сложения по этой формуле получается неестественным.

Произведение по модулю 256

Так же можно рассмотреть вариант с произведением интенсивностей по модулю.

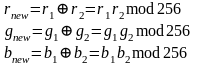
Данная формула также обладает свойством ассоциативности и коммутативности.

Существует нейтральный элемент, относительно операции  равный (1,1,1).

Однако задача нахождения второго цвета участвующего в суммировании не всегда имеет решение, для заданного результата и одного цвета. Но если решение существует, оно находиться крайне быстро.

Результат сложения также как и с суммированием по модулю получается неестественным.

Смещенный вариант мультипликативного смешения цветов

Рассмотрим такую формулу для канала R, для остальных вычисляем аналогично.

При использовании такой формулы у нас существует нейтральный элемент =255. Доказательство этого свойства было проведено на Wolfram Mathematica.

Такая формула является коммутативной и не является ассоциативной.

Например, возьмём следующие 3 цвета: В первом интенсивность красного - 101, в втором – 234, в третьем – 163. В результате получим, что

(R₁R₂)R₃=60

R₁ (R₂R₃)=59

Задача нахождения второго цвета участвующего в суммировании не всегда имеет решение, для заданного результата и одного цвета. Но если решение существует, оно часто оказывается не единственным. Все решения данной задачи находятся достаточно быстро.

Цвет1 Цвет2 Результат Среднее

Рисунок 9. Смешивание цветов.

Также интересно, что в случае смешивания вторичных цветов мы будем получать основные(рис. 10).

Рисунок 10. Сумма вторичных цветов даёт основные