Лабораторная работа № 3 Тарирование расходомера

Краткие теоретические сведения

Работа расходомеров (труба Вентури, мерная диафрагма), ус­танавливаемых на трубопроводах, происходит в соответствии с усло­виями, описанными в уравнениях Бер­нулли и неразрыв­ности.

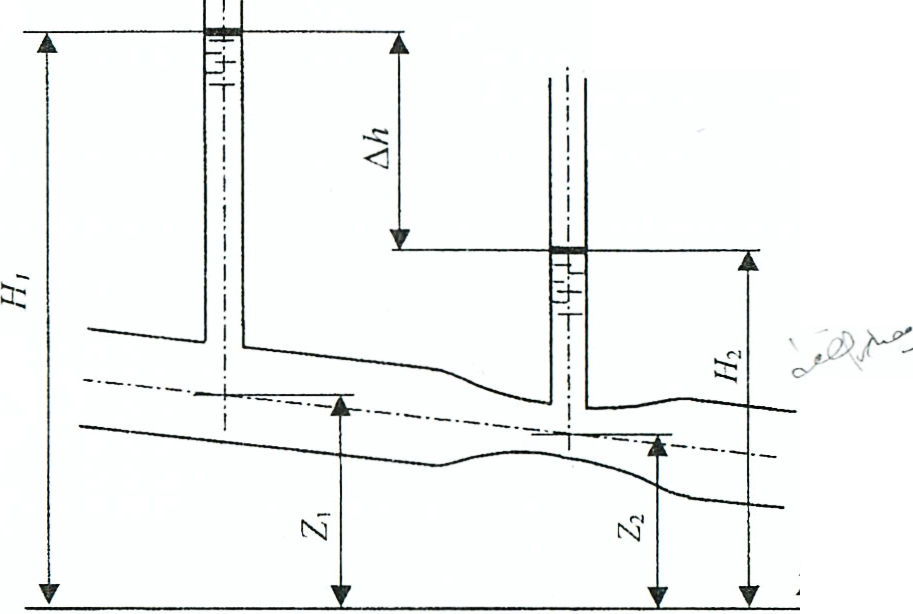
Рис. 3.1

Схема рас­ходомера типа тру­бы Вентури с пье­зометрами, присое­динёнными к широ­кому и узкому её сечениям, пред­ставлена на рис.3.1. На участке расхо­домера сечение по­тока в трубопрово­де сначала сужается, за счет чего средняя скорость жидкости увели­чивается, а затем снова плавно расширяется до первоначальной вели­чины. Возникающее при этом преобразование части статического напора Н = z + р/(ρg) (z - геодезический напор; р/(ρg) - пьезомет­рический напор) в скоростной отражается на уровнях жидкости в пьезометрах H₁ = z₁ + р₁/(ρg) и H₂=z₂+ р₂/(ρg). При этом уро­вень в пьезометре, установленном вузкой части расходомера, будет ниже, чем в пьезометре, установленном в широкой части, на величи­ну Δh, которая включает в себя и потери напора на участке между пьезометрами.

Зависимость между расходом жидкости трубе Q и величи­ной Δh, устанавливаемая на основе уравнений Бернулли и нераз­рывности, имеет вид:

, (3.1)

где С - константа расходомера.

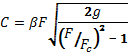
, (3.2)

(величинуС можно также определить опытным путем); β - коэффи­циент расхода; F и F_c - площади поперечных сечений трубы соответ­ственно до сужения и в узком сечении.

Опыт показывает, что в условиях турбулентного режима кон­станты β иС для каждого расходомера есть величины постоянныепри различных значениях Q и Δh. Опытное определение константы расходомераС называется его тарированием. Зависимость между Δh₁ и Δh₂, определяемая на основе уравнений гидростатики, имеет вид:

, (3.3)

где ρ_р - плотность ртути, ρ_р =13600 кг/м3; ρ- плотность жидкости втрубопроводе, кг/м³.

Тарирование расходомеров всех видов, в том числе и трубы Вентури, заключается в опытном определении расходов жидкости через расходомерное устройство на нескольких режимах при одно­временной регистрации разности напоров в широком и узком сече­ниях. В связи с тем, что значения констант расходомера в силу по­грешностей измерений в каждом из опытов могут несколько отли­чаться, необходимо определить средневзвешенное по всем опытам значение этой величины. Для этого могут быть использованы раз­личные способы обработки опытных данных.

Один из таких способов заключается в построении графиков, исследуемой зависимости в логарифмических координатах. Так, про­логарифмировав выражение (3.1), получим:

, (3.4)

откуда следует, что lgQ линейно зависит от lgΔh.

Таким образом, если выразить значения Q иΔh в логарифмах этих величин и отложить их в виде точек на графике (рис.3.2), то между этими точками можно провести прямую линию а, до пересечения сосью lgQ. От­клонения опыт­ных точек от этой прямой (разброс точек) позволяют оце­нить качество эксперимента. Значение коэф­фициента С_граф может быть най­дено по длине отрезка lgC, от­секаемого пря­мойа на оси lgQ.

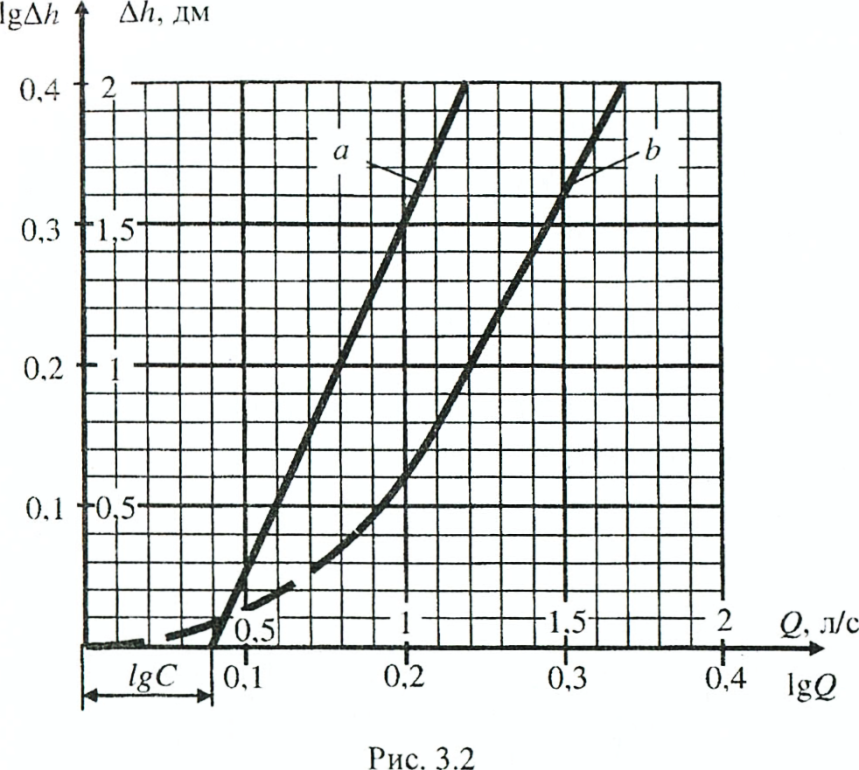
Рис. 3.2

Другим способом обра­ботки опытныхданных является метод наименьших квадратов. Сущность его за­ключается в определении таких значений опытных коэффициентов известной или отыскиваемой функциональной зависимости, при ко­торых сумма квадратов отклонений опытных значений от искомой функции была бы наименьшей. Для определенияС необходимо обеспечить минимум сумм квадратов величин, входящих в выраже­ние:

, (3.5)

Для обеспечения минимума функции М по выражению (3.5) необходимо приравнять нулю ее производную по аргументу dM/dC=0, откуда после математических преобразований получим:

, (3.6)

где n - число опытов.

ЗнаяС, можно построить параболу

(рис.3.2, кри­вая b). Часть параболы, показанная пунктиром, в опытах не исполь­зуется, так как при низких значениях критерия Рейнольдса постоян­ство С не соблюдается.

Описание установки

Опытный трубопровод (рис.3.3) включает в себя два прямо­линейных участка 14 и 17, расширенную часть 16, колено 1, мерную диафрагму 13 и задвижку 10, предназначенную для регулирования расхода в трубопроводе.

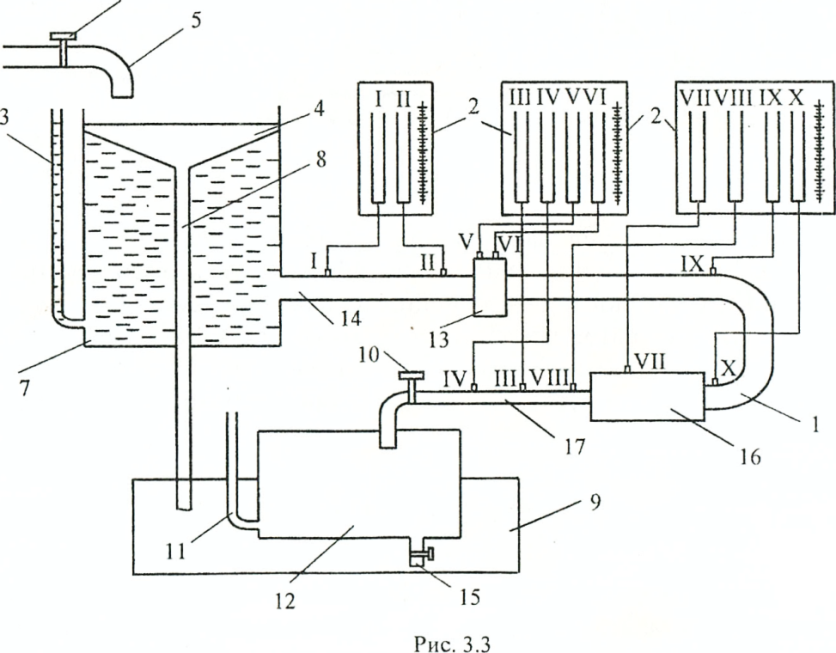
Рис. 3.3

Трубопровод питается от напорного бака 7, снабжённого во­досливом 4 и сливной трубой 8 для поддержания постоянного напо­ра на входе в трубопровод. Поступление воды в бак 7 осуществляет­ся по трубе 5 от лабораторного насоса и регулируется задвижкой 6. Вода, пройдя через опытный трубопровод, сливается в малый слив­ной бак 12 площадью 0,475 м2. Мерный бак снабжён водомерной стеклянной трубкой 11 для определения разности уровней воды в нём до и после замера.

К трубопроводу в десяти сечениях приварены штуцера (по­мечены на схеме рис. 3.3 номерами с I по X), которые соединены резиновыми шлангами со стеклянными пьезометрами, установлен­ными на щитах 2, с миллиметровой градуировкой и началом отсчёта от плоскости, в которой находится ось трубопровода.

Для контроля уровня воды, в баке 7 установлена водомерная стеклянная трубка 3. В процессе опытов на всех режимах нужно следить за тем, чтобы сток через сливную трубу 8 не прекращался, иначе начнётся падение уровня воды в баке 7 и результаты опыта не будут соответствовать тем результатам, которые должны быть полу­чены при постоянном напоре воды на входе в трубопровод.

Порядок выполнения работы

Следует провести не менее трех измерений при каждом уста­новившемся режиме течения жидкости по трубопроводу. Установка каждого режима течения производится руководителем лабораторны­ми работами (с помощью задвижки 10).

1. При помощи крана 15 перекрыть слив воды из бака 12.

2. Зафиксировать начальный уровень воды z\ в баке 12 по показани­ям водомерной стеклянной трубки 11.

3. По истечении 60 секунд измерить конечный уровень воды z₂ в мерном баке 12. Вычислить Δz = z₂- z₁.

4. Снять показания с пьезометров V и VI по нижним точкам мениска с точностью до 1 мм.

5. Спустить воду из мерного бака 12 в зумпф насоса при помощи крана 15.

Формулы и данные для вычислений

Объём воды в мерном баке для каждого замера:

,

где F - площадь мерного бака, (F = 0,475 м²).

Расход воды в каждом замере:

Средний расход воды в каждом из опытов:

Разность показаний пьезометров в каждом из опытов:

Δh = h_V - h_VI .

Значения lgQ_cp и lgΔh определяют по значениям Q_cp и Δh и фиксируют на графике lgΔh = f(lgQ_cp).

Провести прямую с угловым коэффициентом к оси lgQ, рав­ным 0,5. Определить значение lgC (точка пересечения прямой а с осью lgQ и найти С_граф.

Определить значение С' по формуле (3.6). Построить зависи­мость в координатной плоскости Δh = f(Q) при значениях Q, за­данных преподавателем, по формуле:

и нанести на график опытные значения Δh и Q_ср.

Опытные и расчетные величины

Номер опыта	Номер замера	t, с	Δz, м	W, м3	Q, м3/с	Qср, м/c	hV , м	hVI, м
1	2	3	4	5	6	7	8	9

Δh, м		С'	lgQср	lgΔ7	lgC	Cграф
10	11	12	13	14	15	16