7. Проверить с помощью критерия согласия Пирсона гипотезу о том, что выборка извлечена из генеральной совокупности с предполагаемым нормальным законом распределения.

Нулевая гипотеза: Генеральная совокупность, из которой извлечена выборка, распределена по нормальному закону. ( Н₀ : Х

Основная гипотеза ( Н₀ : Х 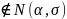, которую мы проверим с помощью критерия Пирсона

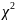
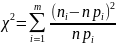
Вероятности рассчитываются с помощью функции Лапласа Ф(x):

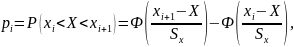
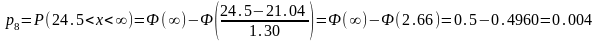
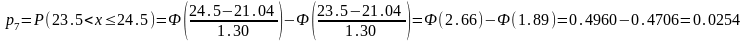
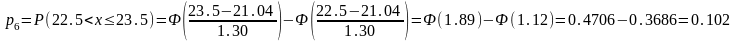
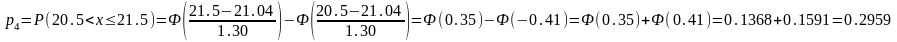
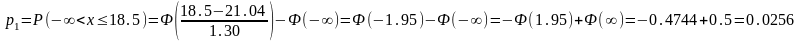
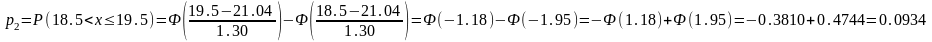
Таблица 5

Расчетная таблица для вычисления

Интервалы (Xi;Xi+1]	Частоты эмпирические ni	Вероятности pi	Теоретич. Частоты n*pi	((ni-n*pi)^2)/(n*pi)
(- ∞ ; 18,5]	3	0,0256	2,56	0,0756
(18,5; 19,5]	8	0,0934	9,34	0,1922
(19,5; 20,5]	18	0,2219	22,19	0,7912
(20,5; 21,5]	41	0,2959	29,59	4,3997
(21,5; 22,5]	18	0,2318	23,18	1,1576
(22,5; 23,5]	8	0,102	10,2	0,4745
(23,5; 24,5]	3	0,0254	2,54	0,0833
(24,5; + ∞]	1	0,004	0,4	0,9000
Сумма	100	1	100	χ^2=8,0742

= 8,0742.

Для определения критических точек распределения необходимо знать уровень значимости(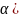 и число степеней свободы( .

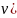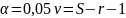
S – число интервалов = 9, r – число параметров = 2.

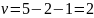
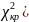2)=5.991

Т.к. 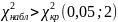, то считаем, что нулевая гипотеза при заданном уровне значимости 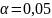не подтверждена.

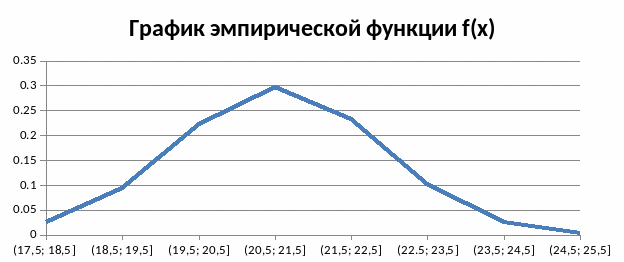
Рисунок 3. График эмпирической функции f(x)

8. В случае принятия гипотезы найти интервальные оценки параметров нормального закона распределения (доверительную вероятность принять равной 0,95).

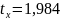
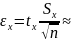1,984* 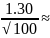0,258

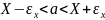
21,04-0,258 < a < 21,04+0,258

20,782 < a < 21,298 – доверительный интервал математического ожидания

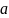
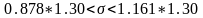
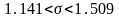- доверительный интервал среднего квадратического отклонения.

9. Провести корреляционный анализ:

1. Составить корреляционную таблицу;

2. Найти выборочный коэффициент корреляции;

3. Проверить значимость выборочного коэффициента корреляции при α = 0,05(Н₀ : ρ = 0), при альтернативной гипотезе Н_α: ρ ≠ 0;

4. Построить корреляционное поле и по характеру расположения точек на нём подобрать общий вид функции регрессии;

5. Найти эмпирические функции регрессии Y на X, X на Y и построить их графики.

Таблица 6

Корреляционная таблица эмпирического распределения двумерной

СВ (X,Y)

	18		19	20		21		22	23	24	25	ny
25	1		5	4								10
35	2		3	4		1						10
45				7		8		2				17
55				3		19		2				24
65						11		4				15
75						2		8	1			11
85								2	5	2		9
95									2	1	1	4
nx	3		8	18		41		18	8	3	1	n = 100
		Sx =			1,30
		Sy =			18,69

Выб. Сред X	Выб. Сред. Y
21,04	56,30
П =	1184,55

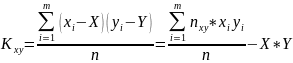
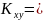20,95

Выборочный коэффициент корреляции:

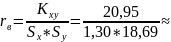0,86

Проверим значимость выбранного коэффициента корреляции.

Нулевая гипотеза:

Альтернативная гипотеза:

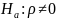
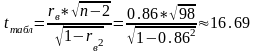
Принятие гипотезы Н_а при уровне значимости 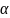=0,05 означает, что выборочный коэффициент корреляции отличается от нуля с ошибкой 7%.

Найдем по таблице квантилей распределения Стьюдента по наиболее употребляемому уровню значимости =0,05 и числу степени свободы v=n-2 квантиль t(1-a;n-2)=t(0.95;98)=1.984.

Так как |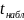 |=16,69>1.984, то нулевая гипотеза отвергается и коэффициент корреляции можно считать существенным, а связь между случайными величинами достоверной, т.е выборочный коэффициент корреляции значимо отличается от нуля. Это означает, что между СВ Х и СВ У существует корреляционная зависимость.

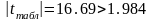
Выборочное уравнение регрессии Y на X:

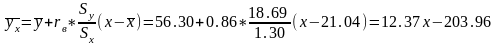
Выборочное уравнение регрессии Х на Y:

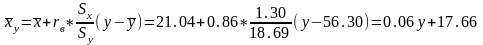
Контроль вычислений: 0.06*12.37 = 0.7422 =

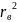
Графики найденных выборочных функций нанесены на рис. 4.