2.3. Порядок проведения пфэ

2.3.1. Порядок постановки опытов

Для оценки дисперсии наблюдений в каждой -й точке факторного пространства проводят опытов. В результате получают значения исследуемого параметра, для которых находят средние значения

.

При этом опыты в одной точке факторного пространства проводят не подряд, а обходят все точки пространства в первой, во второй, ... в -й серии опытов. Для уменьшения влияния внешней среды и неконтролируемых факторов внутри каждой серии точки факторного пространства обходят случайным образом – рандомизируют последовательность опытов. Рандомизацию опытов можно провести с помощью генератора случайных чисел. При формировании задания для выполнения лабораторной работы рандомизация производится ЭВМ автоматически.

2.3.2. Проверка воспроизводимости опытов (однородности дисперсий)

Опыт считается статистически воспроизводимым, если дисперсия параметра однородна (одинакова) в каждой точке факторного пространства. Оценка дисперсии определяется для каждой -й точки факторного пространства по соотношению

.

Гипотезу об однородности дисперсий проверяют с помощью критерия Кохрена. Расчетное значение этого критерия вычисляют по формуле

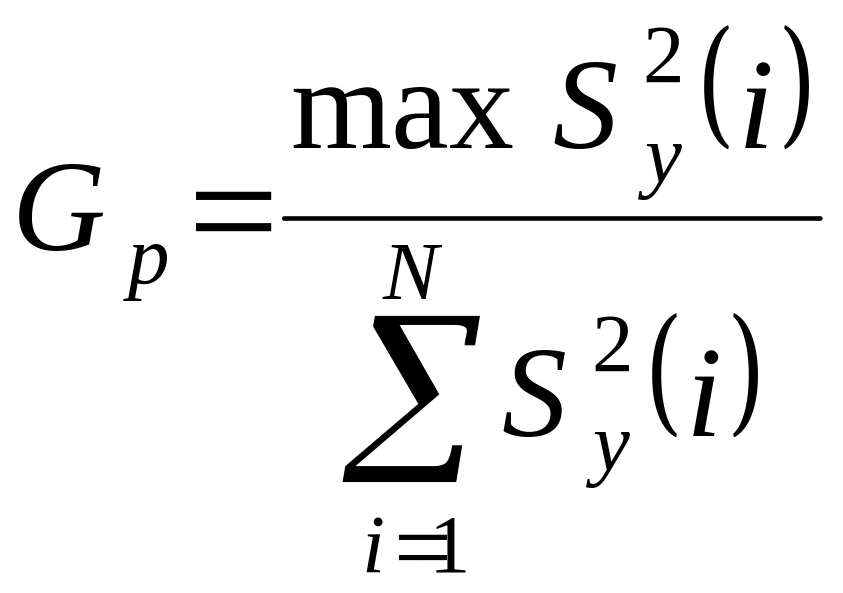, (2.3)

а его критическое значение находят из таблицы распределения Кохрена по числу степеней свободы числителя и знаменателя и уровню значимости (прил. 4). Если гипотеза об однородности принимается, в противном случае отвергается и тогда эксперимент необходимо повторить, изменив условия его проведения (набор факторов, интервал их варьирования, точность измерительных приборов и пр.). Например, если при варьировании какого-то фактора изменение исследуемого параметра сравнимо с погрешностью эксперимента, то интервал варьирования необходимо увеличить примерно на порядок.

2.3.3. Расчет оценок коэффициентов регрессионного уравнения Алгебраический способ

Благодаря предварительной нормировке масштаба факторов, расчет оценок коэффициентов регрессии в ПФЭ сводится к простой арифметической процедуре

.

Матричный способ

Составляем матрицу

.

.Вычисляем информационную матрицу , которая для ПФЭ имеет вид

,

где – единичная диагональная матрица размером , и дисперсионную матрицу

.

Оценки коэффициентов находим по формуле

,

где – вектор средних значений.

2.3.4. Проверка значимости коэффициентов регрессии

Как уже отмечалось выше, гипотеза о статистической значимости (отличии от нуля) коэффициентов регрессии проверяется критерием Стьюдента. Расчетное значение этого критерия определяют как частное от деления модуля оценки коэффициента на оценку его среднеквадратического отклонения

. (2.4)

В ПФЭ благодаря одинаковой удаленности всех экспериментальных точек факторного пространства от центра эксперимента, оценки всех коэффициентов уравнения регрессии независимо от их величины вычисляются с одинаковой погрешностью

где

(2.5)

является оценкой дисперсии единичного наблюдения.

Оценку дисперсии коэффициентов можно найти и с помощью дисперсионной матрицы

,

где – элементы главной диагонали дисперсионной матрицы , которые при ПФЭ все одинаковы и равны .

Критическое значение критерия находят из таблицы распределения Стьюдента по числу степеней свободы и уровню значимости (прил. 5). Если , гипотеза о значимости коэффициента принимается, в противном случае коэффициент считается незначимым и приравнивается к нулю.

Необходимо помнить, что незначимость коэффициента может быть обусловлена неверным выбором интервала варьирования фактора. Поэтому иногда бывает полезным изменить интервал варьирования и провести новый эксперимент.