Тема 2. Механические волны

Вопрос 5. Виды волн в упругой среде. Принцип Гюйгенса. Уравнение волны.

Механической волной называют механические возмущения, распространяющиеся в пространстве и несущие энергию.

Различают два основных вида механических волн: упругие волны (распространение упругих деформаций) и волны на поверхности жидкости.

Упругие волны возникают благодаря связям, существующим между частицами среды: перемещение одной частицы от положения равновесия приводит к перемещению соседних частиц. Этот процесс распространяется в пространстве с конечной скоростью.

Принцип Гюйгенса заключается в том, что каждую точку пространства, до которой дошел волновой фронт, можно считать источником вторичных волн.

Уравнение волны выражает зависимость смещения колеблющейся точки (s), участвующей в волновом процессе, от координаты ее равновесного положения и времени. Для волны, распространяющейся вдоль направления ОХ, эта зависимость записывается в общем виде:

Е сли s и х направлены вдоль одной прямой, то волна продольная, если они взаимно перпендикулярны, то волна поперечная.

Продольные волны могут распространяться в твёрдых телах, жидкостях и газах: во всех этих средах возникает упругая реакция на сжатие, в результате которой появятся бегущие друг за другом сжатия и разрежения среды.

Однако жидкости и газы, в отличие от твёрдых тел, не обладают упругостью по отношению к сдвигу слоёв. Поэтому поперечные волны могут распространяться в твёрдых телах, но не внутри жидкостей и газов.

Выведем уравнение плоской волны. Пусть волна распространяется вдоль оси ОХ (см. рис) без затухания так, что амплитуды колебаний всех точек одинаковы и равны А. Зададим колебание точки с координатой х = 0 (источник колебаний) уравнением

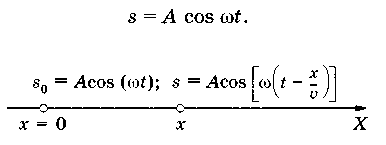
До точки с некоторой произвольной координатой х возмущение от начала координат дойдет через время , поэтому колебания этой точки запаздывают:

Так как время и скорость распространения волны связаны за­висимостью т = x/v, то вместо (5.47) получаем

Это и есть уравнение плоской волны, которое позволяет определить смещение любой точки, участвующей в волновом процес­се, в любой момент времени. Аргумент при косинусе называют фазой волны. Множество точек, имеющих одновременно одинаковую фазу, называют фронтом волны. Для рассмотренного случая фронтом волны будет плоскость х = const (плос­кость, перпендикулярная оси ОХ), всем точкам которой соответствует одновременно одинаковая фаза. Отсюда и название — плоская волна.

Скорость распространения фиксированной фазы колебаний называют фазовой. Предположим, что . Продифференцировав это равенство, получим , откуда

Следовательно, скорость распространения фиксированной фазы колебаний и есть скорость распространения волны.

Кроме фазовой скорости различают еще групповую скорость, которую вводят тогда, когда реальная волна не может быть представлена одним гармоническим уравнением, а является суммой группы синусоидальных волн.

Длиной волны называют расстояние между двумя точками, фазы которых в один и тот же момент времени отличаются на . Она равна расстоянию, пройденному волной за период колебания: