Тема 6. Биоэлектрогенез

Вопрос 18. Электрический диполь и его поле.

Электрическим диполем (диполем) называют систему, со­стоящую из двух равных, но противоположных по знаку точечных электрических зарядов, расположенных на некото­ром расстоянии друг от друга (плечо диполя).

О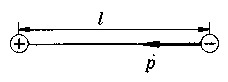 сновной характеристикой диполя (см. рис.) является его электрический момент (дипольный момент) — вектор, равный произведению заряда на плечо диполя l, направленный от отрицательного заряда к положительному:

Единицей электрического момента диполя является кулон-метр.

Поместим диполь в однородное электрическое поле напряженностью (см. рис.)

Н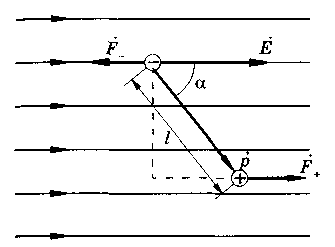 а каждый из зарядов диполя действуют силы и , эти силы равны по модулю, противоположно направлены и создают момент пары сил. Как видно из рисунка, он равен

или в векторной форме

Таким образом, на диполь в однородном электрическом поле действует момент силы, зависящий от электрического момента и ориентации диполя, а также напряженности поля.

Рассмотрим теперь диполь в неоднородном электрическом поле. Предположим, что диполь расположен вдоль силовой линии (см. рис.). На него действуют силы

где Е₊ и Е_- — напряженности поля соответственно в месте нахожде­ния положительного и отрицательного зарядов (на рис. Е_- > Е₊). Значение равнодействующей этих сил

Введем отношение (Е_- - Е₊)/1, характеризующее среднее изменение напряженности, приходящееся на единицу длины плеча диполя. Так как обычно плечо невелико, то приближенно можно считать где dE/dx — производная от напряженности электрического поля по направлению оси ОХ, являющаяся мерой неоднородности электрического поля вдоль соответствующего направления. Отсюда следует, что

тогда формулу для F можно представить в виде

Итак, на диполь действует сила, зависящая от его электрического момента и степени неоднородности поля dE/dx. Если диполь ориентирован в неоднородном электрическом поле не вдоль силовой ли­нии, то на него дополнительно действует еще и момент силы. Таким образом, свободный диполь ориентируется вдоль силовых линий и втягивается в область больших значений напряженности поля.

Д о сих пор рассматривался диполь, помещенный в электрическое поле, однако сам диполь также является источником поля. Запишем выражение для электрического потенциала поля, созданного диполем, в некоторой точке А, удаленной от зарядов соответственно на расстояния r и r₁ (см. рис.):

Обычно предполагают, что l<<r, l<<r₁, тогда r ≈ r₁ и

где α — угол между вектором и направлением от диполя на точку А (см. рис.). Окончательно получаем

Вопрос 19. Физические основы электрокардиографии. Отведения при экг (стандартные, усиленные, грудные).

Живые ткани являются источником электрических потенциа­лов (биопотенциалов).

Регистрация биопотенциалов тканей и органов с диагностиче­ской (исследовательской) целью получила название электрографии. Такой общий термин употребляется сравнительно редко, более распространены конкретные названия соответствующих диагностических методов: электрокардиография (ЭКГ) — регистрация биопотенциалов, возникающих в сердечной мышце при ее возбуждении, электромиография — метод регистрации биоэлектрической активности мышц, электроэнцефалография (ЭЭГ) — метод регистрации биоэлектрической активности головного мозга и др.

В большинстве случаев биопотенциалы снимаются электродами не непосредственно с органа (сердце, головной мозг), а с других, соседних тканей, в которых электрические поля этим органом создаются. В клиническом отношении это существенно упрощает са­му процедуру регистрации, делая ее безопасной и несложной.

Физический подход к электрографии заключается в создании (выборе) модели электрического генератора, которая соответствует картине «снимаемых» потенциалов. В связи с этим здесь возникают две фундаментальные теоретические задачи: расчет по­тенциала в области измерения по заданным характеристикам электрического генератора (модели) — прямая задача, расчет ха­рактеристик электрического генератора по измеренному потенциалу — обратная задача.

Дальнейшие конкретные рассмотрения физических вопросов электрографии сделаны на примере электрокардиографии.

Одной из основных задач теоретической электрокардиографии является вычисление распределения трансмембранного потенциала клеток сердечных мышц по потенциалам, измеренным вне сердца. Однако даже чисто теоретически такую задачу решить невозможно, так как одно и то же «внешнее» проявление биопотен­циалов сердца будет при разном «внутреннем» их распределении.

Физический (биофизический) подход к выяснению связи между биопотенциалами сердца и их внешним проявлением заключается в моделировании источников этих биопотенциалов.

Все сердце в электрическом отношении представляется как некоторый эквивалентный электрический генератор либо чисто умозрительно (гипотетически), либо в виде реального устройства как совокупность электрических источников в проводнике, имеющем форму человеческого тела. На поверхности проводника при функционировании эквивалентного электрического генератора будет электрическое напряжение, которое в процессе сердечной деятельности возникает на поверхности тела человека. Предполагают, что среда, окружающая сердце, безгранична и однородна с удельной электрической проводимостью у.

В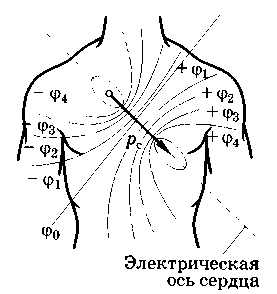 мультипольном эквивалентном генераторе сердца основная часть в потенциал на поверхности тела человека вносится его дипольной составляющей. Иначе говоря, моделировать электрическую деятельность сердца вполне допустимо, если использовать дипольный эквивалентный электрический генератор.

Д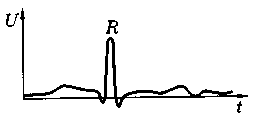 ипольное представление о сердце лежит в основе теории отведений Эйнтховена. Согласно ей, сердце есть диполь с дипольным моментом р_с, который поворачивается, изменяет свое положение и точку приложения (изменением точки приложения этого вектора часто пренебрегают) за время сердечного цикла.

На рис. показаны положения вектора р_с и эквипотенциальных линий для момента времени, когда дипольный момент максимален; это соответствует «зубцу» R на электрокардиограмме (нижн. рис.).

По терминологии физиологов, разность биопотенциалов, реги­стрируемая между двумя точками тела, называют отведением. Точками для формирования отведений (их всего 12 при записи стандартной ЭКГ) выступают вершины треугольника Эйнтховена (стандартные отведения), центр треугольника (усиленные отведения) и точки, расположенные непосредственно над сердцем (грудные отведения).

Стандартные отведения. Вершины треугольника Эйнтховена - электроды на обеих руках и левой ноге. Определяя разницу потенциалов электрического поля сердца между двумя вершинами треугольника, говорят о регистрации ЭКГ в стандартных отведениях (рис. А): между правой и левой руками - I стандартное отведение, между правой рукой и левой ногой - II стандартное отведение, между левой рукой и левой ногой - III стандартное отведение.

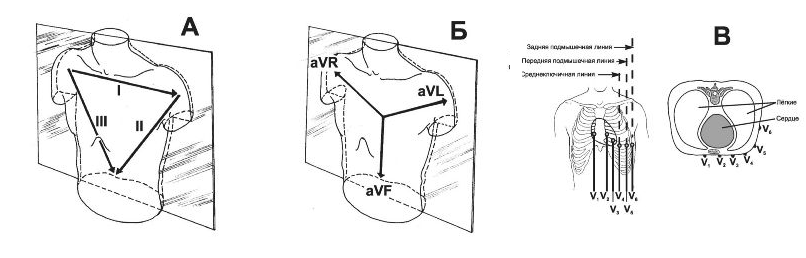Усиленные отведения от конечностей. В центре треугольника Эйнтховена при суммировании потенциалов всех трёх электродов формируется виртуальный «нулевой», или индифферентный, электрод. Разницу между нулевым электродом и электродами в вершинах треугольника Эйнтховена регистрируют при снятии ЭКГ в усиленных отведениях от конечностей (рис. Б): aVL - между «нулевым» электродом и электродом на левой руке, aVR - между «нулевым» электродом и электродом на правой руке, aVF - между «нулевым» электродом и электродом на левой ноге. Отведения называются усиленными, поскольку их приходится усиливать ввиду небольшой (по сравнению со стандартными отведениями) разницы потенциалов электрического поля между вершиной треугольника Эйнтховена и «нулевой» точкой.

Грудные отведения - точки поверхности тела, расположенные непосредственно над сердцем на передней и боковой поверхности грудной клетки (рис. В). Устанавливаемые на эти точки электроды называются грудными, равно как и отведения, формирующиеся при определении разницы: потенциалов электрического поля сердца между точкой установления грудного электрода и «нулевым» электродом, - грудные отведения V₁-V₆.