Тема 1. Механические колебания

Вопрос 1. Гармонические колебания. Скорость и ускорение гармонического колебания. Энергия гармонического колебания

Гармоническими называются колебания, совершаемые по закону синуса или косинуса. В общем случае гармоническое колебание величины s описывается уравнением типа

где A – амплитуда колебания, т.е. максимальное значение колеблющейся величины; ω – круговая (циклическая) частота; φ – начальная фаза колебания в момент времени t=0; - фаза колебания в момент времени t.

Фаза колебания определяет значение колеблющейся величины в данный момент времени. Так как косинус меняется в пределах от -1 до +1, то колеблющаяся величина может принять значения от –А до –А.

Период колебаний T — это время одного полного колебания.

Ч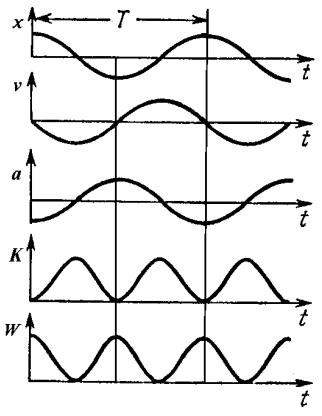 астота колебаний ν — это величина, обратная периоду: ν = 1/T. Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.

Одному полному колебанию отвечает приращение фазы, равное 2π радиан: , откуда .

Пусть материальная точка совершает прямолинейные гармонические колебания вдоль оси х около положения равновесия принятого, за начало координат. Тогда для колеблющейся точки

Смещение

Скорость

Ускорение

Амплитуды скорости и ускорения равны и . Фаза скорости отличается от фазы смещения на , а фаза ускорения на π.

Сила, действующая на колеблющуюся материальную точку массой m равна .

Вопрос 2. Затухающие колебания. Декремент затухания. Апериодические колебания.

В реальном случае на колеблющееся тело действуют силы сопротивления (трения), характер движения изменяется по сравнению с гармоническими колебаниями, и колебание становится затухающим. Обычно полагают, что при не очень больших амплитудах и частотах сила сопротивления пропорциональна скорости движения, и естественно, направлена противоположно скорости: , r- коэффициент трения (сопротивления), характеризующий свойства среды оказывать сопротивление.

Уравнение колебаний с учетом затухания записывается в виде:

,

г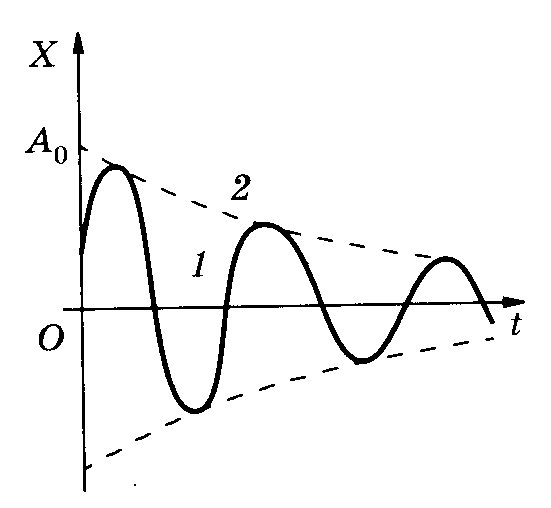 де A₀ – амплитуда колебания; ω – круговая (циклическая) частота; φ₀ – начальная фаза колебания в момент времени t=0; β – коэффициент затухания ( ). Круговая частота ω связана с частотой собственных колебаний системы (без затухания) ω₀ следующим образом .

На рис сплошной кривой 1 изображен график функции x(t) при , а штриховой линией 2 изображено изменение амплитуды: .

Период затухающих колебаний зависит от коэффициента затухания и определяется формулой: .

При очень малом трении ( ) период затухающего колебания близок к периоду незатухающего свободного колебания: .

Быстрота убывания амплитуды колебаний определяется коэффициентом затухания β: чем сильнее тормозящее действие среды, тем больше β и тем быстрее уменьшается амплитуда. На практике, однако, степень затухания часто характеризуют декрементом затухания, понимая под этим величину, равную отношению двух последовательных амплитуд, разделенных интервалом времени, равным периоду колебаний, и его натуральным логарифмом (логарифмический декремент затухания):

.

Коэффициент затухания и логарифмический декремент затухания связаны достаточно простой зависимостью: .

П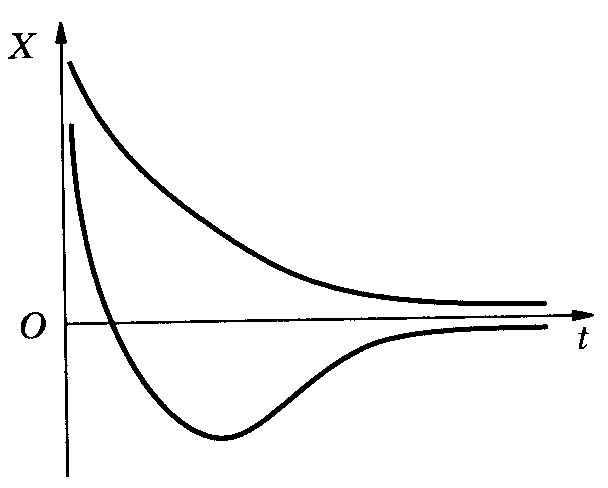 ри сильном затухании ( ) круговая частота является мнимой величиной. Движение в этом случае уже не будет периодическим и называется апериодическим. Возможные апериодические движения представлены в виде графиков на рис.