
- •1. Зачем статистика врачу?
- •2. Введение.
- •3. Выборочный метод наблюдения – основной метод научного исследования.
- •4. Задачи статистического описания переменных.
- •5. Определение числовых характеристик случайных величин по результатам выборочного наблюдения.
- •6. Построение статистического ряда распределения случайной переменной по результатам выборочного наблюдения.
- •7. Закон нормального распределения случайной величины.
- •Лабораторная работа №1 исследование статистических функций.
- •Зачем статистика врачу?
- •Лабораторная работа №2 статистические методы обработки данных.
- •Лабораторная работа№ 3 точечное и интервальное оценивание параметров распределений
- •Часть 1. Точечное оценивание.
- •Часть 2. Интервальное оценивание.
- •Лабораторная работа№ 3 проверка статистической гипотезы о виде распределения
- •Лабораторная работа № 4 основы регрессионного и корреляционного анализа
5. Определение числовых характеристик случайных величин по результатам выборочного наблюдения.
Числовые характеристики переменных подразделяют на три вида:
характеристики положения;
характеристики рассеяния;
характеристики вида распределения.
К характеристикам положения относятся:
среднее арифметическое значение -
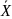 ;
;медиана - Me;
мода - Mo;
среднее геометрическое значение – XG;
среднее гармоническое значение – XH;
к характеристикам рассеяния значений переменной относятся:
минимальное – XMIN и максимальное - XMAX значение;
размах вариационного ряда: R= XMAX - XMIN;
дисперсия – S2;
среднее квадратичное (стандартное) отклонение: S;
25% и 75% процентили (квартили) и межквартильный размах;
95% доверительный интервал истинного среднего значения;
Вид распределения характеризуют коэффициенты:
ассиметрия – A;
эксцесс – E.
По числовым характеристикам судят о соответствии эмпирического распределения теоретическому нормальному распределению. Распределение можно оценивать как близкое к нормальному, если:
среднее арифметическое, геометрическое и гармоническое значения незначительно различаются друг от друга, а также с модой и медианой;
минимальные и максимальные значения примерно равноудалены от среднего значения;
стандартизованные коэффициенты ассиметрии и эксцесса по абсолютной величине меньше 2.
6. Построение статистического ряда распределения случайной переменной по результатам выборочного наблюдения.
Эмпирическое распределение переменной представляется в виде статистического (вариационного) ряда распределения, характеризующего связь между возможными значениями переменной и частостью их наблюдения в выборке. Для построения статистического ряда распределения в выборке необходимо иметь несколько десятков и более наблюдений, которые группируются в m интервалов.
Выбор интервалов группировки возможен:
по формуле Стерджесса:
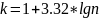 ,
,
по эмпирическим выработанным рекомендациям:
Объем выборки, n |
Число интервалов, m |
25 – 40 |
5- 6 |
40 – 60 |
6 – 8 |
60 – 100 |
7 – 10 |
100 – 200 |
8 – 12 |
Более 200 |
10 – 15 |
Подготовку данных для статистического ряда распределения выполняют в следующем порядке:
в зависимости от числа наблюдений n выбирают число интервалов ряда m;
определяют размах вариационного ряда R= Xmax - Xmin;
рассчитывают длину интервала (шаг) h=R/m;
определяют границы и средние точки интервалов;
подсчитывают частоту наблюдений, частость и накопленные частоты для каждого интервала.
По данным статистического ряда распределения строят гистограмму и кумулятивную линию распределения. По виду гистограммы и кумулятивной линии делают предварительные выводы о характере и соответствии эмпирического распределения определенному теоретическому.
