4.3. Классификация основных видов статистических графиков

Для графического представления статистических данных используются самые раз- нообразные виды графиков (рис. 4.2 и 4.3). Их можно классифицировать по разным при- знакам: характеру графического образа, способу построения и назначению (содержанию).

_{Статистические графики по форме графического образа}

_{Линейные} Плоскостные

_{Объемные}

Статистические кривые

Полосовые

Круговые

Поверхностные распределения

Секторные

Фигурные

_{Столбиковые}

Фоновые

_{Квадратные}

Точечные

_{Рис. 4.2. Классификация статистических графиков по форме графического образа}

Статистические графики по способу построения и задачам изображения

_{Диаграммы}

_{Статистические карты}

Диаграммы сравнения

Диаграммы динамики

Картограммы

фоновые точечные

Диаграммы структуры

Картодиаграммы

Диаграммы взаимосвязи

Диаграммы степени выполнения плана

Рис. 4.3. Классификация статистических графиков

_{по способу построения и содержанию изображаемых данных}

44

_{ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ}

По характеру графического образа различают графики объемные, линейные и пло-

скостные (рис. 4.2).

По способу построения графики можно разделить на диаграммы и статистические карты (рис. 4.3).

Диаграмма представляет собой чертеж, показывающий соотношение статистиче-

ских данных при помощи разнообразных геометрических и изобразительных средств.

Статистические карты предназначены для графического изображения одноимен- ных показателей, относящихся к разным территориям. Для этого в основу изображения берется географическая карта. Изображение на карте статистических данных называется картограммой или картодиаграммой.

По содержанию или назначению можно выделить графики сравнения в простран- стве, графики относительных величин (структуры, динамики и т.п.), графики вариацион- ных рядов, графики взаимосвязанных показателей и графики размещения по территории (рис. 4.3).

4.4. Диаграммы сравнения

Различные виды диаграмм применяются для сравнения одноименных статистиче- ских данных, характеризующих разные территории или объекты. Наиболее распростра- нённым видом таких диаграмм являются столбиковые диаграммы. Они представляют собой график, в котором различные величины представлены расположенными в высоту прямоугольниками («столбиками») одинаковой или разной высоты. Столбиковые диа- граммы применяются для сравнения некоторых объектов во времени.

Построение такого рода диаграмм требует только одной вертикальной масштаб-

ной шкалы, которая определяет высоту каждого столбика.

Масштабная шкала должна начинаться с нуля, быть непрерывной и на ней записы-

ваются лишь круглые или округленные значения.

Столбики должны быть даны на некотором, одинаковом для всех расстоянии или вплотную друг к другу. Ширина столбиков берется произвольной. На шкале должна быть указана единица измерения.

При выборе масштаба надо рассчитать так, чтобы максимальное число было представлено на графике.

Пример. Требуется изобразить с помощью столбиковой диаграммы данные о тру- доустройстве граждан органами государственной службы занятости региона (цифры ус- ловные): в 2004 г. трудоустроено 2822 чел.; в 2003 г. – 2398 чел.; в 2002 г. – 2406 чел.; в

2001 г. – 2218 чел. Примем масштаб: 500 чел. соответствует 1 см. Тогда высота первого столбика (трудоустройство в 2001 г.) будет равна 4,4 см (1 см*2218/500), высота второго (в 2002 г.)-4,8 см; высота третьего (в 2003 г.)-4,79 см; высота четвертого (в 2004 г.)-5,6 см. Наглядность данной диаграммы достигается сравнением высоты столбиков (рис. 4.4).

На рис. 4.5 с помощью столбиковой диаграммы показана структура посевных пло- щадей сельхозпредприятий N-ой области РФ за 2004 г. (цифры условные). На этой диа- грамме столбики располагаются вплотную по группам объектов в пространстве.

Масштаб принят такой, что каждым 5000 тыс. га соответствует отрезок в 1 см.

Если прямоугольники, изображающие показатели, расположить не по вертикали, а по горизонтали, то диаграмма получит название ленточной. В качестве примера приведем полосовую диаграмму сравнения, характеризующую данные о реализации минеральных удобрений сельхозпредприятиями в N-ом регионе за 2001-2004 гг. (рис. 4.6).

45

_{ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ}

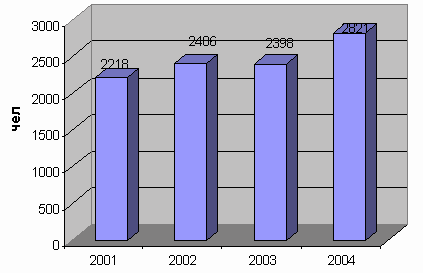
Рис. 4.4. Динамика трудоустройства граждан органами государственной службы занятости в регионе за 2001-2004 гг.

35000

30000

25000

20000

15000

10000

5000

₀

9767

5675

33503

2540

Зерновые культуры

Картофель

Овощи

Кормовые культуры

Рис. 4.5. Структура посевных площадей сельхозпредпртятий N-ой области РФ в 2004 г.

Рис. 4.6. Динамика реализации минеральных удобрений сельскохозяйственными предприятиями в N-ом регионе за 2001-2004 гг.

Иногда разница между наименьшими и наибольшими значениями сравниваемых данных настолько велика, что установление подходящего масштаба для столбиков или

46

_{ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ}

полос оказывается затруднительным. В этих случаях вместо столбиковой (полосовой) диаграммы целесообразно применить плоскостную (двухмерную) диаграмму – квадрат- ную или круговую. Принцип построения этих диаграмм заключается в том, что величины сравниваемых данных изображаются площадями квадратов или кругов. Иными словами, площади квадратов (кругов) должны быть пропорциональны величинам изображаемых явлений, но сами площади квадратов (кругов) пропорциональны квадратам их сторон (ра- диусов). Следовательно, стороны квадратов или радиусов кругов должны быть пропор- циональны корням квадратным из величин изображаемых статистических данных.

Пример. Необходимо с помощью квадратной диаграммы изобразить реализацию молочных продуктов предприятиями розничной торговли в одном из регионов за 2004 г. по следующим данным:

Товар	Товарооборот, млн. руб
творог	11
сметана	16
молоко	19

Для построения квадратной диаграммы сначала извлечем квадратные корни из чи- сел: √11=3,32; √16=4; √19=4,36. Затем установим масштаб, например, примем 1см-1,5 млн. руб. Тогда сторона 1-го квадрата составит 2,2см (3,32:1,5); 2-го – 2,7см; 3-го – 2,9см (4,36:1,5). Далее строим квадраты.

Для правильного построения диаграммы квадраты необходимо расположить на одинаковом расстоянии друг от друга, а в каждой фигурке указать числовое значение, ко- торое она изображает, не приводя масштаба измерения (рис. 4.7).

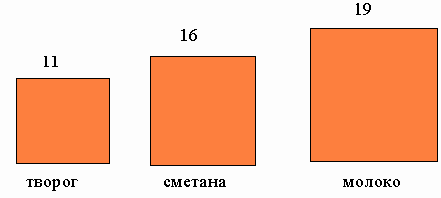
Рис. 4.7. Реализация молочных продуктов предприятиями розничной торговли в одном из регионов в 2004 г., млн. руб.

Круговая диаграмма строится аналогично квадратной с той разницей, что находим величину радиуса для каждого круга.

Пример. По данным об иностранных инвистициях в экономику РФ по основным странам-инвесторам за 2002 г. построить круговые диаграммы:

Страна	Германия	Кипр	Швейцария
Инвестиции, млн долларов США (x)	4001	2327	1349
√x	63,25	48,24	36,7
R	3,2	2,4	1,8

Примем 1 см – 20 млн. долл., тогда радиус 1-го круга будет 3,2 см (63,25:20),

2-го круга – 2,4 см; 3-го круга – 1,8 см. (рис. 4.8).

47

_{ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ}

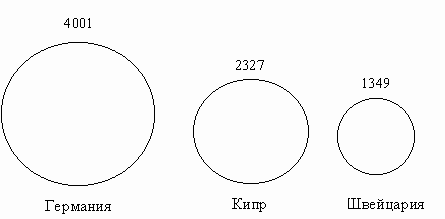
Рис. 4.8. Иностранные инвестиции в экономику РФ

по основным странам-инвесторам за 2002 г., млн. долларов США

Диаграммы, предназначенные для популяризации, иногда строятся в виде стан- дартных фигур-рисунков, характерных для изображаемых статистических данных, что де- лает диаграмму более выразительной, привлекает к ней внимание. Такие диаграммы на- зываются фигурными или изобразительными. Каждая фигурка имеет одинаковый раз- мер и принимается за определённую величину изображаемых статистических данных.

Пример. Изобразим в виде фигурной диаграммы количество проданных магнито-

_{фонов в N-ом регионе за 2001-2004 гг. по следующим данным:}

Годы	2001	2002	2003	2004
Продано, тыс. шт.	1977	862	875	995

Примем условно за один знак 300 тыс. штук магнитофонов. Тогда продажа магни- тофонов в 2001 г. в размере 1977 тыс. штук будет изображена в количестве 6,6 магнито- фона, в 2002 г. – 2,9 магнитофона, в 2003 г. – 2,9 магнитофона, в 2004 г. – 3,3 магнитофона (рис. 4.9).

_{Рис. 4.9. Динамика продажи магнитофонов за 2001-2004 гг.}

48

_{ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ СТАТИСТИЧЕСКОЙ ИНФОРМАЦИИ}

Недостаток фигурных диаграмм заключается в том, что во многих случаях прихо- дится либо округлять изображаемые данные, либо изображать, кроме целых фигур, их части, размер которых на глаз оценивать трудно.

Для графического изображения трех взаимосвязанных показателей, один из кото- рых равен произведению двух других, российский статистик проф. В.Е.Варзар предложил использовать прямоугольную диаграмму, названную им «статистическим знаком». В на- стоящее время такие диаграммы часто называют знаком Варзара.

Знак Варзара строится в виде прямоугольника, основание которого пропорцио- нально одному показателю-сомножителю, а высота – второму показателю сомножителю. Тогда произведение этих показателей, т.е. третий показатель, будет изображаться площа- дью прямоугольника.

Пример. Имеются следующие данные в 2001 г. по всему миру:

ВНП – 46403 млрд. долл.

ВНП на душу населения – 7570 долл.

Средняя численность населения – 6,1298 млрд. чел.

Нужно изобразить эти данные с помощью знака Варзара (рис. 4.10). Взаимосвязь этих по-

казателей можно представить в виде:

П рои з в о д с т в о Ср е д н я я Об щ е е

ВН П на ду ш у X ч и сл ен н о ст ь = пр о и з в о д с т в о н асел е н и я н асел ен и я ВН П

₈₀₀₀

7000

6000

5000

₄₀₀₀

⁷⁵⁷⁰ 46403

- общее производство ВНП

₃₀₀₀

₂₀₀₀

1000

_{1 2 3}

6129,8

_{4 5}

Средняя численность населения, млрд. чел.

_{6 7}

Рис. 4.10. Зависимость общего производства ВНП от производства ВНП на душу населения и средней численности населения мира в 2001 г.