
- •1.Основные понятия.
- •3) Кинематические цепи. Кинематические соединения
- •4) Механизмы плоские и пространственные. Число свободы механизма и его определение.
- •8,Рычажный механизм.
- •9) Понятие термина машина, классификация машин
- •10 Основные методы кинематического анализа.
- •11 Графоаналитический метод кинематического анализа - метод планов скоростей и ускорений.
- •1 2 Построение планов ускорений.
- •1 5 Свойства планов скоростей.
- •1 8 Приведение сил и масс. Динамические модели машины.
- •22 Виды зубчатых механизмов
10 Основные методы кинематического анализа.
Задачей кинематического анализа является изучение движения звеньев механизма вне зависимости от сил, действующих на них.
В результате по заданному закону движения ведущего звена определяются положения, угловые скорости и ускорения ведомых звеньев, а также перемещения, скорости, ускорения отдельных точек.
Кинематическое исследование схем механизмов производится аналитическими и графическими методами.
Аналитические методы позволяют с требуемой точностью установить аналитически функциональную зависимость кинематических параметров механизма от параметров звеньев. Эти методы отличаются сложностью и трудоемкостью. Их применение оправдывается при использовании ЭВМ. Графические методы исследования разделяются на:
1. Метод построения кинематических диаграмм.
2. Метод планов скоростей и ускорений. Метод построения кинематических диаграмм основан на графическом изображении перемещений, скоростей или ускорений отдельных точек звеньев в функции времени или перемещений ведущего звена.
Переход от графиков перемещений к графикам скоростей и ускорений производится путем графического дифференцирования, а обратно - графическим интегрированием.
Э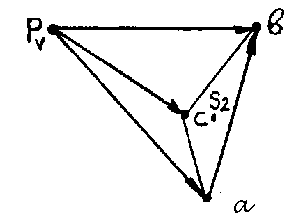 тот
метод дает наглядное представление об
изменении кинематических параметров
во времени.
тот
метод дает наглядное представление об
изменении кинематических параметров
во времени.
М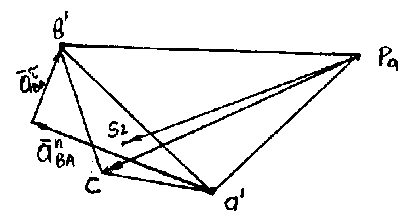 етод
планов скоростей и ускорений позволяет
при наличии планов положений механизма
определить скорости и ускорения любых
точек механизма для любого момента
времени.Кинематические исследования
этим методом начинаются с построена
плана механизма, т. е. изображение его
кинематической схемы в выбранном
масштабе длины звеньев
етод
планов скоростей и ускорений позволяет
при наличии планов положений механизма
определить скорости и ускорения любых
точек механизма для любого момента
времени.Кинематические исследования
этим методом начинаются с построена
плана механизма, т. е. изображение его
кинематической схемы в выбранном
масштабе длины звеньев
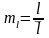 [
[ ],где
],где
 -истинный размер звена,
-истинный размер звена,
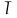 -его масштабное изображение в мм.
-его масштабное изображение в мм.
11 Графоаналитический метод кинематического анализа - метод планов скоростей и ускорений.
Пусть дан кривошипно - ползунный механизм, схема которого показана на рис. 2.7. Известны длины звеньев, положение механизма и постоянная угловая скорость кривошипа W1. Требуется определить скорости и ускорения точек А, В, С, и угловые скорость и ускорение шатуна W2 и E2.
2.3.1
Построение планов скоростей. Определяем
скорость точки А кривошипа по формуле
 ,Здесь
,Здесь
 - длина кривошипа ОА
в М.
- длина кривошипа ОА
в М.
Назначаем
полюс плана скоростей РV
и из него перпендикулярно кривошипу
ОА откладываем отрезок PV
a
(рис2.8), представляющий собой вектор
скорости точки А при масштабном
коэффициенте плана скоростей![]() .
который определяется выражением
.
который определяется выражением
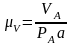 где
PV
a
-длина вектора в мм на плане скоростей.
Для определения скорости точки В
движение шатуна разложим на переносное
поступательное со скоростью точки А и
относительное вращательное вокруг
этой точки. Такое разложение движения
описывается векторным уравнением.
где
PV
a
-длина вектора в мм на плане скоростей.
Для определения скорости точки В
движение шатуна разложим на переносное
поступательное со скоростью точки А и
относительное вращательное вокруг
этой точки. Такое разложение движения
описывается векторным уравнением.
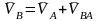
В таблицу под уравнением внесены данные о величине и направлении векторов. Неизвестными здесь являются величины векторов.
VB
и VBA
при известных их направлениях. Такое
уравнение может быть решено графически
построением плана скоростей. Из полюса
PV
проводится направление вектора
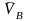 ,
а из конца вектора скорости точки А -
направление вектора
,
а из конца вектора скорости точки А -
направление вектора
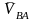 .
На пересечении этих прямых находится
конец вектора скорости точки В (точка
"в" плана скоростей). Теперь можно
найти скорость любой другой точки.
Например, для скорости точки С можно
записать два векторных уравнения:
.
На пересечении этих прямых находится
конец вектора скорости точки В (точка
"в" плана скоростей). Теперь можно
найти скорость любой другой точки.
Например, для скорости точки С можно
записать два векторных уравнения:
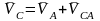 ,
,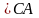
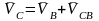
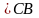
Проведя из точек а и в плана скоростей прямые, перпендикулярные отрезки АВ и ВС шатуна найдем конец вектора скорости точки С, начало его лежит в полюсе РV. Величины скоростей точек А, В, С в м/с определяются выражениями:
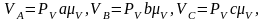
Т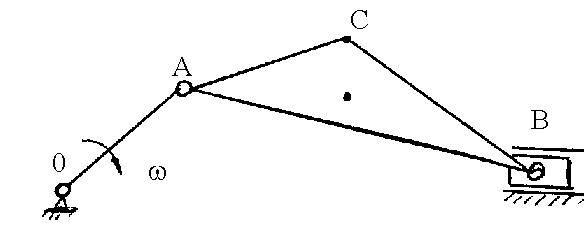 аким
образом, если у звена известны величина
и направление скорости одной точки и
направление скорости (траектория)
другой точки, то можно определить
скорость любой его точки.
аким
образом, если у звена известны величина
и направление скорости одной точки и
направление скорости (траектория)
другой точки, то можно определить
скорость любой его точки.
