
- •1,2.Перше правило лопіталя
- •3.Друге правило Лопіталя
- •4. Розкритття невизначеностей
- •5. Формула Тейлора з залишковим членом у формі Пеано
- •6. Формула Тейлора з залишковим членом у формі Лагранжа
- •7.Формула Тейлора через диференціали.
- •8. Формула Маклорена
- •9. Формула Тейлора для Многочлена
- •15. Бином Ньютона
- •16. Дослдження функції за допомогою похідної
- •18. Означення (локальний максимум функції)
- •19. Дослідження функції на локальний екстремум за допомогою першої похідної.
- •21. Випуклі функції
- •22. Точки перегину
- •27. Властивості опуклих функцій.
- •28. Поняття асимптоти вітки кривої та графіка функції.
- •29. Відшукання вертикальної асимптоти вітки кривої та графіка функції.
- •31,32,33. Парні та непарні функції, їх геометричний зміст, приклади, властивості
- •34,35. Періодичні функції та їх властивості. Основний період.
- •36. Загальна схема дослідження функцій для побудови графіка.
- •7. Метод підстановки
- •8. Інтеграли вигляду
- •10. Інтегрування ірраціональних функцій за допомогою тригонометричних підстановок
- •11. Диференціальні біноми. Теорема Чебишова. Інтегрування диференціальних біномів.
- •13,14 Елементарні дроби першого і другого типу та їх інтегрування.
7. Метод підстановки
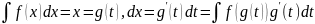
Часто
в студентській практиці зустрічаються
інтеграли, які не можуть бути зведені
в простий спосіб за основними формулами.
З введенням нової незалежної змінної,
в таких випадках, вдається перетворити
підінтегральний вираз ![]() .
Це дозволяє звести інтеграл до табличного
або до такого, спосіб обчислення якого
може бути відомий. Заміна змінної
інтегрування є основою методу, що
називається методом підстановки.
Незалежну змінну замінюють за формулою
.
Це дозволяє звести інтеграл до табличного
або до такого, спосіб обчислення якого
може бути відомий. Заміна змінної
інтегрування є основою методу, що
називається методом підстановки.
Незалежну змінну замінюють за формулою ![]() ,
де
,
де ![]() –диференційована
функція від
–диференційована
функція від ![]() .
Після цього знаходять
.
Після цього знаходять
![]()
і
інтеграл ![]() перетворюють
до такого
перетворюють
до такого
![]()
Якщо
одержаний інтеграл з новою змінною
інтегрування
буде
знайдено, то перетворивши результат в
зворотньому напрямку до змінної![]() ,
використовуючи залежність
,
відшукаємо вираз заданого інтегралу.
,
використовуючи залежність
,
відшукаємо вираз заданого інтегралу.
На перший погляд вище наведені формулювання методу виглядають не такими простими, як хотілося. Але повірте, що за даним методом стоять не такі важкі математичні перетворення. Розглянувши приклади, які наведені нижче і попрактикувавши на інших, у Вас все получиться. Якщо ні – надсилайте важкі приклади нам, а ми зі своєї сторони спробуємо їх розв'язати і опублікувати в наступних статтях. Отже переходимо до прикладів.
8. Інтеграли вигляду
де
R - раціональна функція своїх аргументів
x, у,...,v; ![]() -
цілі числа, обчислюються за допомогою
підстановки
-
цілі числа, обчислюються за допомогою
підстановки
![]() ,
де s спільний знаменник дробів
,
де s спільний знаменник дробів ![]()
9.
10. Інтегрування ірраціональних функцій за допомогою тригонометричних підстановок
Розглянемо
інтегрування виразів повністю залежать
від тригонометричних функцій, над якими
виконуються лише арифметичні операції.
Такі
вирази називаються раціональними функціями від
тригонометричних функцій і в даному
випадку позначаються ![]()
Теорема. Інтеграл
виду ![]() за
допомогою підстановки
за
допомогою підстановки ![]() перетвориться
в інтеграл від раціонального дробу.
Для
доказу висловимо
перетвориться
в інтеграл від раціонального дробу.
Для
доказу висловимо ![]() ,
, ![]() і
і ![]() через
через ![]() :
:
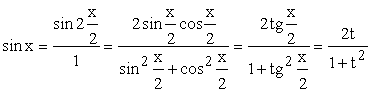 ;
;
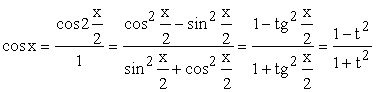 ;
;
![]() .
.
У
даному виразі раціональні дроби підставлені
в раціональну функцію. Так як над ними
виконуються лише арифметичні операції,
то в результаті виходить також раціональний
дріб. Отже, раціональну функцію від
тригонометричних функцій можна
проінтегрувати, перетворивши її в
раціональну дріб.
Підстановка
, ![]() ,
, 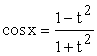 ,
, ![]()
11. Диференціальні біноми. Теорема Чебишова. Інтегрування диференціальних біномів.
Интегрирование
дифференциального бинома. Выражение
вида ![]() ,
где
,
где ![]() –
рациональные числа, а
–
рациональные числа, а ![]() –
действительные числа, называется
дифференциальным биномом.
–
действительные числа, называется
дифференциальным биномом.
Рассмотрим интеграл
![]() . (6.43)
. (6.43)
Как показал Чебышев П.Л., интеграл (16.43) рационализируется лишь в следующих трех случаях:
если ![]() –
целое число, то применяется подстановка
–
целое число, то применяется подстановка ![]() ,
где
,
где ![]() – наименьшее
общее кратное знаменателей дробей
– наименьшее
общее кратное знаменателей дробей ![]() и
и ![]() ;
;
если ![]() –
целое число, то применяется подстановка
–
целое число, то применяется подстановка ![]()
![]() ,
где
,
где ![]() –
знаменатель дроби
;
–
знаменатель дроби
;
если ![]() –
целое число, то применяется подстановка
–
целое число, то применяется подстановка ![]() ,
где
–
знаменатель дроби
.
,
где
–
знаменатель дроби
.
Во всех остальных случаях интеграл (16.43) через элементарные функции не выражается.
12.


13,14 Елементарні дроби першого і другого типу та їх інтегрування.
1
тип:
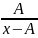
2
тип: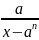
Їх інтегрування:
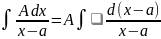 =
A ln
=
A ln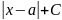 - 1 тип
- 1 тип
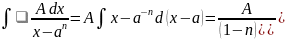 -
2 тип
-
2 тип
