18. Означення (локальний максимум функції)

Функція f : D  R, (D  R^m) має в точці A  D:

1. локальний максимум, якщо існує окіл O (A,r) точки A такий, що 

   1. O (A,r)  D,

   2. для всіх x O (A,r): f (x)  f(A).

2. строгий локальний максимум, якщо існує окіл O (A,r) точки A такий, що

   1. O (A,r)  D,

   2. для всіх x O (A,r), відмінних від A: f (x) < f (A).

Необхідною умовою існування екстремуму в точці   диференційованої функції   є рівність нулю її похідної:  .

Теорема (необхідна умова існування локального екстремуму)

Нехай f : D R, (D  R^m) і A  D. Якщо

a) f досягає локального екстремуму в точці A,

b) існують частинні похідні   

то A є стаціонарною точкою f.

19. Дослідження функції на локальний екстремум за допомогою першої похідної.

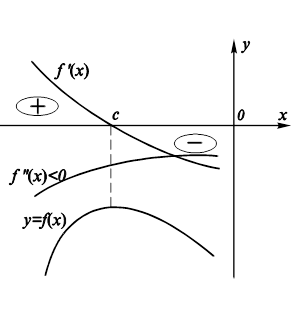
Функция y=f(x) в точке x0 имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x0, т. е. если существует такая окрестность точки x0, что для всех x≠x0, принадлежащих этой окрестности, имеет место неравенство f(x)<f(x0).>f(x0).  Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.  Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.  Теорема 1. (Необходимое условие существования экстремума. ) Если дифференцируемая функция y=f(x) имеет в точке x=x0 экстремум, то ее производная в этой точке обращается в нуль.  Доказательство. Пусть для определенности в точке x0 функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x0+ Δx)<f(x0),>0 при x<x0> x0, то x0 – точка максимума;  при x<x0>0 при x> x0, то x0 – точка минимума.  Доказательство. Предположим сначала, что при переходе через x0 производная меняет знак с плюса на минус, т. е. при всех x, близких к точке x0 f '(x)>0 для x< x0, f '(x)<0 для x> x0. Применим теорему Лагранжа к разности f(x) - f(x0) = f '(c)(x- x0), где c лежит между x и x0.  Пусть x < x0. Тогда c< x0 и f '(c)>0. Поэтому f '(c)(x- x0)<0 и, следовательно,  f(x) - f(x0)<0,т. е. f(x)< f(x0).  Пусть x > x0. Тогда c> x0 и f '(c)<0. Значит f '(c)(x- x0)<0. Поэтому f(x) - f(x0)<0,т. е. f(x) < f(x0).  Таким образом, для всех значений x достаточно близких к x0 f(x) < f(x0). А это значит, что в точке x0 функция имеет максимум.  Аналогично доказывается вторая часть теоремы о минимуме.  Проиллюстрируем смысл этой теоремы на рисунке. Пусть f '(x1)=0 и для любых x, достаточно близких к x1, выполняются неравенства  f '(x)<0 при x< x1, f '(x)>0 при x> x1.

20. Дослідження функції на локальний екстремум за допомогою похідних 2 та вищих порядків.

Исследование функции с помощью второй производной

Вторая производная функции, если она существует, может быть так же эффективно использована для исследования на экстремум, определения промежутков выпуклости и вогнутости ее графика, отыскания точек перегиба.

ТЕОРЕМА 1 (ВТОРОЕ ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА). Если для функции   в точке  производная  , А в ее окрестности   непрерывна, причем    , то эта точка является точкой ее максимума (минимума).

ДОКАЗАТЕЛЬСТВО.

Пусть в точке с выполняется равенство

И имеет место неравенство

Будучи непрерывной, вторая производная сохраняет свой знак при х, Близких к с. Поэтому для этих x

Но вторая производная функции есть производная от первой производной

Рис. 11.17. Возможное взаимное расположение графиков функций  ,   И   в окрестности точки Максимума.

Это условие является достаточным признаком для существования экстремума, но не является необходимым. Почему?

Следовательно,   есть функция убывающая. По условию теоремы,  . Это означает, что   левее точки с Положительна, а правее – отрицательна. Переходя к самой функции  , можно утверждать, что левее точки С она возрастает, а правее – убывает, то есть с – точка ее максимума, что и требовалось доказать. Аналогично доказывается теорема в случае минимума. На рис. 11.17 приведен возможный вариант взаимного расположения графиков функций ,   И   в окрестности точки с.

Данная теорема может оказаться удобной, когда знак   определяется легко. Однако ее недостаток в сравнении с первым достаточным условием экстремума функции очевиден: не все точки, подозрительные на экстремум, могут быть исследованы с помощью данной теоремы. Она неприменима в случаях, когда в точке с первая производная функции обращается в бесконечность или же не определена и, конечно, когда   не существует.

Сформулируем без доказательства некоторое обобщение данной теоремы для случая, когда функция имеет производные порядка  .

ТЕОРЕМА 2. Если функция   в некоторой окрестности точки С имеет производную до (n+1)-го порядка, непрерывную в самой точке С, причем   то при четном (n+1) функция  имеет максимум, если   и минимум, если  .