
- •1,2.Перше правило лопіталя
- •3.Друге правило Лопіталя
- •4. Розкритття невизначеностей
- •5. Формула Тейлора з залишковим членом у формі Пеано
- •6. Формула Тейлора з залишковим членом у формі Лагранжа
- •7.Формула Тейлора через диференціали.
- •8. Формула Маклорена
- •9. Формула Тейлора для Многочлена
- •15. Бином Ньютона
- •16. Дослдження функції за допомогою похідної
- •18. Означення (локальний максимум функції)
- •19. Дослідження функції на локальний екстремум за допомогою першої похідної.
- •21. Випуклі функції
- •22. Точки перегину
- •27. Властивості опуклих функцій.
- •28. Поняття асимптоти вітки кривої та графіка функції.
- •29. Відшукання вертикальної асимптоти вітки кривої та графіка функції.
- •31,32,33. Парні та непарні функції, їх геометричний зміст, приклади, властивості
- •34,35. Періодичні функції та їх властивості. Основний період.
- •36. Загальна схема дослідження функцій для побудови графіка.
- •7. Метод підстановки
- •8. Інтеграли вигляду
- •10. Інтегрування ірраціональних функцій за допомогою тригонометричних підстановок
- •11. Диференціальні біноми. Теорема Чебишова. Інтегрування диференціальних біномів.
- •13,14 Елементарні дроби першого і другого типу та їх інтегрування.
1,2.Перше правило лопіталя
Нехай
виконані умови:
1. функції f(х) та g(х) визначені
і диференційовані в колі точки х0;
2.
частка цих функцій ![]() в
точці х0 має
невизначеність вигляду
в
точці х0 має
невизначеність вигляду ![]() або
або ![]() ;
3.
існує
;
3.
існує ![]() .
Тоді
існує
.
Тоді
існує ![]() і
виконує рівність:
і
виконує рівність:
![]() (1)
(1)
Аналогічно правило Лопіталя застосовується також й у випадку правосторонніх границь та границь взагалі.
3.Друге правило Лопіталя
Теорема
2.
(друге
правило Лопіталя).
Нехай функції
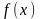 і
і
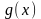 диференційовані
на інтервалі (a;b);
диференційовані
на інтервалі (a;b);
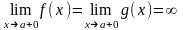 і
і
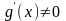 на (a;b). Тоді, якщо існує (нескінченна або
скінченна) границя
на (a;b). Тоді, якщо існує (нескінченна або
скінченна) границя
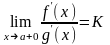 ,
то границя
,
то границя
 також існує і
також існує і
 .
.
Зауваження, подані до теореми 1, залишаються в силі і для теореми 2.
Трапляється,
що для похідних
 і
і
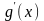 виконуються умови однієї з теорем, тоді
правила Лопіталя можна застосовувати
повторно:
виконуються умови однієї з теорем, тоді
правила Лопіталя можна застосовувати
повторно:
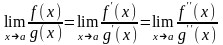 .
.
Відповідно,
знаходження
 називають розкриттям
невизначеностей
типу
називають розкриттям
невизначеностей
типу
 або
або
 .
.
Невизначеність
 ,
тобто добуток
,
тобто добуток
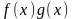 ,
де
,
де
 ,
зводиться до вигляду
або
за формулами
,
зводиться до вигляду
або
за формулами
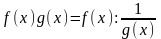 або
або
 .
.
4. Розкритття невизначеностей
Нехай ![]() і
і ![]() ,
тоді
,
тоді
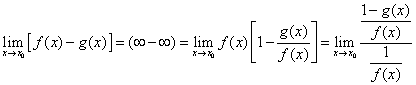 (3)
За
умовою
(3)
За
умовою ![]() при
при ![]() ,
тому
,
тому ![]() при
.
Якщо
при
.
Якщо ![]() не
прямує до 0 при
,
то границя в правій частині (3) не існує,
а тому і границя лівої частини (3) не
існує.
Якщо
не
прямує до 0 при
,
то границя в правій частині (3) не існує,
а тому і границя лівої частини (3) не
існує.
Якщо ![]() при
,
то вираз
при
,
то вираз 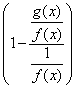 має
невизначеність
.
має
невизначеність
.
2.
Нехай ![]() ,
,
тоді
,
,
тоді ![]() має
невизначеність вигляду
має
невизначеність вигляду ![]() при
.
В
цьому випадку поступають так:
при
.
В
цьому випадку поступають так:
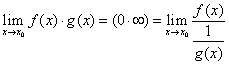
3.
Нехай ![]() ,
, ![]() при
.
Тоді
при
.
Тоді ![]() має
невизначеність вигляду
має
невизначеність вигляду ![]() .
Позначимо
.
Позначимо ![]() .
Шляхом логарифмування цієї рівності
одержимо:
.
Шляхом логарифмування цієї рівності
одержимо:
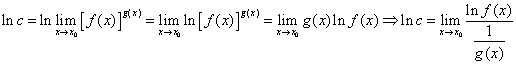
5. Формула Тейлора з залишковим членом у формі Пеано
Існує f’(x0)є R f-диференційована в т x0 f(x)=f(x0)+f(x0)(x-x0)+o(x-x0) -> x -> 1/x . Нехай існує f^ n (x0) , тоді f(x)=f(x0)+f(x0)(x-x0)+f^n(x0)/2!*(x+x0)^2 + f^n(x0)/3!(x-x0)^3+…+f^n(x0)/n!(x-x0) + o(x-x0)^n , x ->x0
Д-ння: Tn(x0,…) – многочлен , залишковий член у формы Пеано. Позн g(x) = f(x)-Tn . g(x0)=f(x0) – Tn(x0,xd) = f’(x)-f’(x)f’’(x-x0)-f^n(x-x0)/2! / f^n(x-x0)^n-1 / (n-1)!; g’(x0)=0 . g’’(x)=f’’(x) - f’’(x0)(x-x0 ) -… f^n(x0)/(n-2)! , (x-x0)^n-2
G’’(x0)=0; g^n(x0)=0. G^(n-1)(x) – диф в т. x0 . g^(n-1)(x)=g^(n-1)(x0) + g^n(x0)(x-x0)+o(x-x0) , x->x0
6. Формула Тейлора з залишковим членом у формі Лагранжа
Теорема (формула Тейлора з залишковим членом у формі Лагранжа)
Якщо функція f
(1) має неперервну похідну порядку n -1 на відрізку [x0, x],
(2) має похідну порядку n на інтервалі (x0, x),
то існує точка c (x0, x) така, що
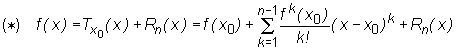
![]()
а Tx0(x) є многочлен Тейлора порядку n -1.
Формула (*) називається формулою Тейлора з n-им залишковим членом у формі Лагранжа, а вираз
![]()
називається n-им залишковим членом у формі Лагранжа.
Зауваження
• Вигляд залишкового члена у формулі Тейлора правильний для інтервалу [x, x0] (тоді x0 (x, x0)).
В обидвох випадках: x0 > x або x0 < x залишковий член можна подати простою формулою
![]()
Залишкові члени у формі Лагранжа
![]()
![]()
послабимо припущення:
Нехай функція
 має
має 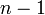 похідних
у деякому околі точки
похідних
у деякому околі точки 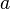
І
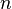 похідних
у самій точці
похідних
у самій точці
тоді:
![]()
