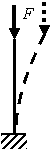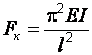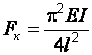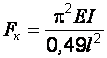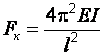21. Практические расчеты стержней на устойчивость

Расчет стержней на продольную нагрузку осуществляется: 1)на прочность 2)на устойчивость

При назначении размеров сжатого стержня в первую очередь необходимо заботится о том, чтобы он в процессе эксплуатации не потерял устойчивость. Поэтому напряжения в стержне должны быть обязательно меньше критических

. (а)

Здесь — сжимающая сила в стержне, — критическое напряжение, — коэффициент запаса устойчивости, — площадь поперечного сечения брутто (без учета ослабленного сечения отверстиями, вырубками и

т.д. Они мало влияют на величину критической силы).

При расчете растянутых стержней на прочность применяется формула

(б)

Поделим (а) на (б) и обозначим отношение правых частей через

или ,

где — коэффициент уменьшения основного расчетного сопротивления при продольном изгибе. Оно называется “коэффициентом продольного изгиба” и зависит от гибкости стержня.

т.е. .

Расчетная формула для сжатых стержней принимает вид

, или

, (8.11)

где берется по таблице.

Расчетная формула для сжатого стержня внешне совпадает с расчетной формулой для растянутого стержня. Она удобна тем, что позволяет пользоваться одним допускаемым напряжением, как для растянутого, так и для сжатого стержня.

Подбор сечения стержня производится методом последовательных приблежений.

Критические силы при разных закреплениях сжатых стержней

Схемы стержней и формы потери устойчивости
Коэффициент	1	2	0,7	0,5
Критическая сила FК

 

Если критическое напряжение превышает предел пропорциональности материала, то потеря устойчивости сопровождается появлением пластических деформаций и критическую силу вычисляют по формуле Ясинского

 

,

где  – площадь поперечного сечения стержня;  и  – коэффициенты, зависящие от материала стержня;  – гибкость стержня.

22. Продольно-поперечный изгиб.

Рассмотрим нагружение прямого шарнирно закреплённого стержня продольной силой F и системой поперечных сил. Такой вид нагружения принято называть продольно-поперчным изгибом. Обозначим у(z) прогиб балки в сечении c абсциссой z. Воспользуемся дифференциальным уравнением упругой линии балки, в котором изгибающий момент можно рассматривать как сумму моментов поперечных сил и момента продольной силы F·y. Полный прогиб у складывается из прогиба у_п от поперечных сил и дополнительного прогиба у-у_п от осевой силы F.

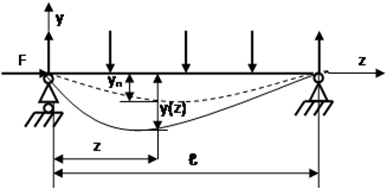
Полный прогиб у больше суммы прогибов, возникающих при раздельном действии поперечных и продольных сил, так как при действии только силы F прогиб

равен нулю. Следовательно, в данном случае принцип независимости действия сил не применим.

( 8.5 ) .

Разделим левую и правую части выражения (9.5) на EI :  (8.6)

Так как , то подставив это значение в (8.6), получим  ,

или  (8.7).

Для упрощения решения предполагается, что дополнительный прогиб по длине балки изменяется по синусоиде, т.е.

(8.8).

Это допущение позволяет получить точные результаты при действии на балку поперечной нагрузки, направленной в одну сторону.

С учётом (8.8) выражение (8.7) примет вид: .

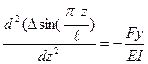После двухкратного дифференцирования этого уравнения получим  ,  или .

Из этого равенства на ходим  .

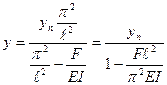Выражение =F_э совпадает в формулой Эйлера, тогда  у= (8.9)

Необходимо отличать эйлерову силу F_э от критической силы F_кр, вычисляемой по формуле Эйлера для стержней большой гибкости ( ). Эйлерова сила F_э не зависит от гибкости стержня.

Из формулы (8.9), что отношение является критерием жесткости при продольно поперечном изгибе. Если → 0, жёсткость балки велика и . При → 1 жёсткость мала, балка очень гибкая и у→ ∞, т.е., прогибы многократно возрастают по сравнению с .

Формула (8.9) достаточно точная при F≤F_кр.