Чaстота́ — физическая величина, характеристика периодического процесса, равна количеству повторений или возникновения событий (процессов) в единицу времени. Рассчитывается, как отношение количества повторений или возникновения событий (процессов) к промежутку времени, за которое они совершены^[1]. Стандартные обозначения в формулах — ν, f или F.

Единицей измерения частоты в Международной системе единиц (СИ) является герц (русское обозначение: Гц; международное:Hz), названный в честь немецкого физика Генриха Герца.

Частота обратно пропорциональна периоду колебаний: f = 1/T.

Частота	1 мГц (10−3 Гц)	1 Гц (100 Гц)	1 кГц (103 Гц)	1 МГц (106 Гц)	1 ГГц (109 Гц)	1 ТГц (1012 Гц)
Период	1 кс (103 с)	1 с (100 с)	1 мс (10−3 с)	1 мкс (10−6 с)	1 нс (10−9 с)	1 пс (10−12 с)

Частота, как и время, является одной из наиболее точно измеряемых физических величин: до относительной точности 10^−17[2].

В природе известны периодические процессы с частотами от ~10⁻¹⁶ Гц (частота обращения Солнца вокруг центра Галактики) до ~10³⁵ Гц (частота колебаний поля, характерная для наиболее высокоэнергичных космических лучей).

В квантовой механике частота колебаний волновой функции квантовомеханического состояния имеет физический смысл энергии этого состояния, в связи с чем система единиц часто выбирается таким образом, что частота и энергия выражаются в одних и тех же единицах (иными словами, переводный коэффициент между частотой и энергией — постоянная Планка в формуле E = hν — выбирается равным 1).

Глаз человека чувствителен к электромагнитным волнам с частотами от 4·10¹⁴ до 8·10¹⁴ Гц (видимый свет); частота колебаний определяет цвет наблюдаемого света. Слуховой анализатор человека воспринимает акустические волны с частотами от 20 Гц до 20 кГц. У различных животных частотные диапазоны чувствительности к оптическим и акустическим колебаниям различны.

Отношения частот звуковых колебаний выражаются с помощью музыкальных интервалов, таких как октава, квинта, терция и т. п. Интервал в одну октаву между частотами звуков означает, что эти частоты отличаются в 2 раза, интервал в чистую квинту означает отношение частот ³⁄₂. Кроме того, для описания частотных интервалов используется декада — интервал между частотами, отличающимися в 10 раз. Так, диапазон звуковой чувствительности человека составляет 3 декады (20 Гц — 20 000 Гц). Для измерения отношения очень близких звуковых частот используются такие единицы, как цент(отношение частот, равное 2^1/1200) и миллиоктава (отношение частот 2^1/1000).

Содержание

  [убрать] 

• 1 Мгновенная частота и частоты спектральных составляющих

• 2 Циклическая частота

• 3 Частота дискретных событий

• 4 Частота вращения

• 5 Другие величины, связанные с частотой

• 6 Единицы измерения

• 7 Метрологические аспекты

  • 7.1 Эталоны

  • 7.2 Вычисления

  • 7.3 Методы измерения

    • 7.3.1 Стробоскопический метод

    • 7.3.2 Метод биений

    • 7.3.3 Применение частотомера

    • 7.3.4 Непрямые методы измерения

• 8 Примеры

  • 8.1 Электромагнитное излучение

  • 8.2 Звук

  • 8.3 Промышленная частота переменного тока

• 9 См. также

• 10 Примечания

• 11 Литература

• 12 Ссылки

Мгновенная частота и частоты спектральных составляющих[править | править исходный текст]

Периодический сигнал характеризуется мгновенной частотой, являющейся (с точностью до коэффициента) скоростью изменения фазы, но тот же сигнал можно представить в виде суммы гармонических спектральных составляющих, имеющих свои (постоянные) частоты. Свойства мгновенной частоты и частоты́ спектральной составляющей различны^[3].

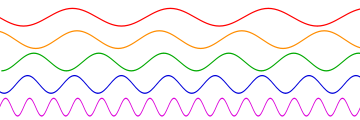
Синусоидальные волны различных частот, нижние волны имеют более высокие частоты, чем верхние. Горизонтальная ось представляет время.

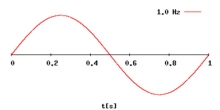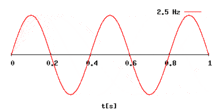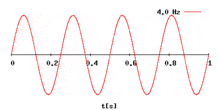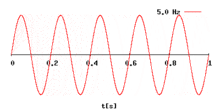
Изменение частоты

Циклическая частота[править | править исходный текст]

Основная статья: Угловая частота

В теории электромагнетизма, теоретической физике, а также в некоторых прикладных электрорадиотехнических расчётах удобно использовать дополнительную величину — циклическую (круговую, радиальную, угловую) частоту (обычно обозначается ω). Углова́я частота́ (синонимы: радиальная частота, циклическая частота, круговая частота) — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота в радианах в секунду выражается через частоту f (выражаемую в оборотах в секунду или колебаниях в секунду), как ω = 2πf.

В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей: ω = 360°·f.

Численно циклическая частота равна числу циклов (колебаний, оборотов) за 2π секунд. Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC-контура равна   тогда как обычная резонансная частота  В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.

В механике при рассмотрении вращательного движения аналогом циклической частоты служит угловая скорость.

Частота дискретных событий[править | править исходный текст]

Частота дискретных событий (частота импульсов) — физическая величина, равная числу дискретных событий, происходящих за единицу времени. Единица частоты дискретных событий — секунда в минус первой степени (с⁻¹, s⁻¹), однако на практике для выражения частоты импульсов обычно используют герц.

Частота вращения[править | править исходный текст]

Частота вращения — это физическая величина, равная числу полных оборотов за единицу времени. Единица частоты вращения — секунда в минус первой степени (с⁻¹, s⁻¹), оборот в секунду. Часто используются такие единицы, как оборот в минуту, оборот в час и т. д.

Другие величины, связанные с частотой[править | править исходный текст]

• Ширина полосы частот — 

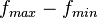
• Частотный интервал — 

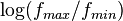
• Девиация частоты — 

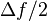
• Период — 

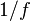
• Длина волны — 

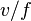
• Угловая скорость (скорость вращения) — 

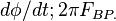
Единицы измерения[править | править исходный текст]

В системе СИ единицей измерения является герц. Единица была первоначально введена в 1930 году Международной электротехнической комиссией^[4], а в 1960 году принята для общего употребления 11-й Генеральной конференцией по мерам и весам, как единица СИ. До этого в качестве единицы частоты использовался цикл в секунду (1 цикл в секунду = 1 Гц) и производные (килоцикл в секунду, мегацикл в секунду, киломегацикл в секунду, равные соответственно килогерцу, мегагерцу и гигагерцу).