Испытания конструкций
Задача №11
Для определения фактического момента инерции (Jx). Были проведены статические испытания стальной консольной балки балкона при нагрузке F=15кН. Вылет балки L=2,5м. Замеренный максимальный прогиб консоли у=3,0см. Найти момент инерции сечения балки если Е= 2,1·105 МПа.
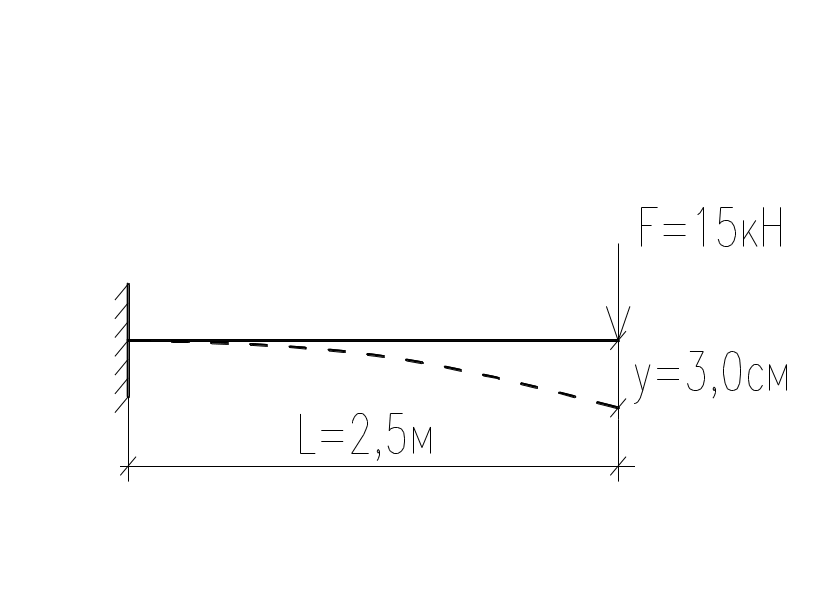
Решение:
Момент инерции сечения консольной балки нагруженной сосредоточенной силой может быть определен из выражения:
Задача №12
При вводе здания в эксплуатацию были проведены статические испытания стальной шарнирно-опертой балки перекрытия равномерно распределенной нагрузкой. Пролет балки равен L=6,0м. Интенсивность распределительной нагрузки q=2кН/м. Замеренный прогиб в середине пролета балки равен у=9,2мм. Определить конструктивную поправку Ку и прогиб балки от распределенной нагрузки q=10кН/кг, если Е= 2,1·105МПа, Jx=1840·10-4м2.
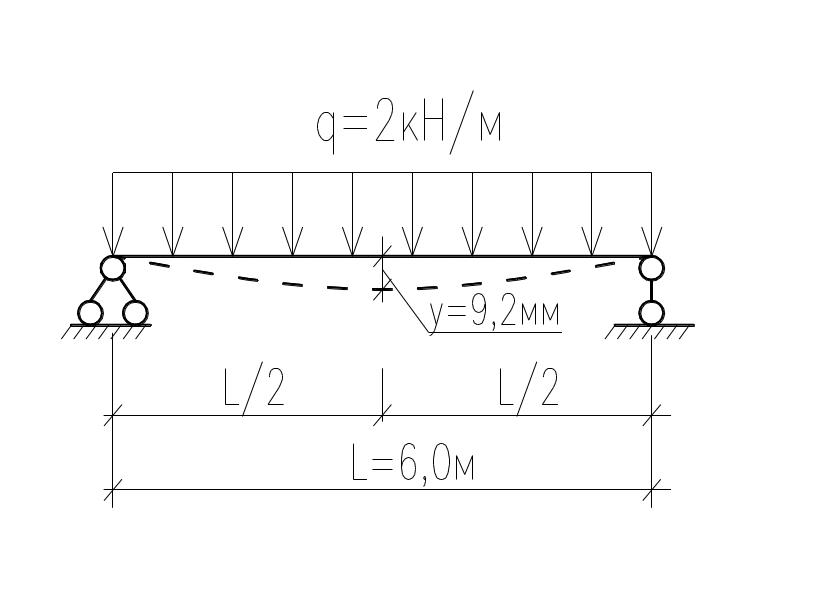
Решение:
Аналитические выражения для определения прогиба в седине пролета опертой балки с равномерно распределенной нагрузкой, выражается формулой:
Конструктивная поправка Kу:
Фактический прогиб балки в середине пролета при нагрузке q=10кН/м будет равным:
Задача №13
Определить изгибную жесткость (EJx) и модуль упругости материала балки, если измеренный в середине пролета прогиб при интенсивности распределенной нагрузке q=8,5 кН/м составил у=0,01м.
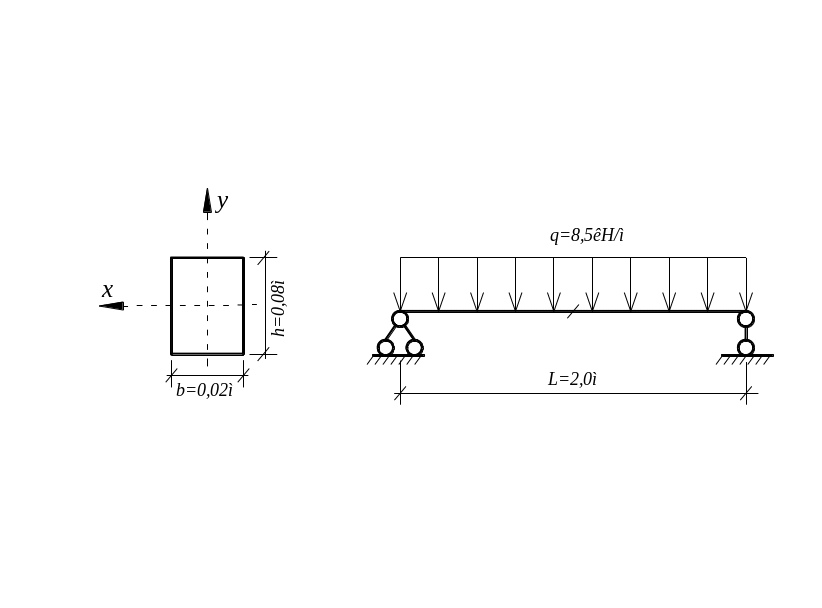
Решение:
Изгибная жесткость для шарнирно-опертой балки, нагруженной равномерно распределенной нагрузкой, может быть определена по формуле:
Модуль упругости материала балки равен:
Динамические испытания конструкции
Задача №14
Определить приведенный модуль упругости ж/б однопролетной балки с шарнирным опиранием. Длина балки L=6м. Размеры прямоугольного сечения h=0,45м, b=0,2м. Вес одного кубометра бетона балки P=2200кг. При динамическом испытании балки определена частота первой формы колебаний f0=50Гц.
Считать (ЕJ)ст=(EJ)дин.
Решение:
Приведенный модуль упругости для балки с шарнирным опиранием может быть определен из формулы:
f0T=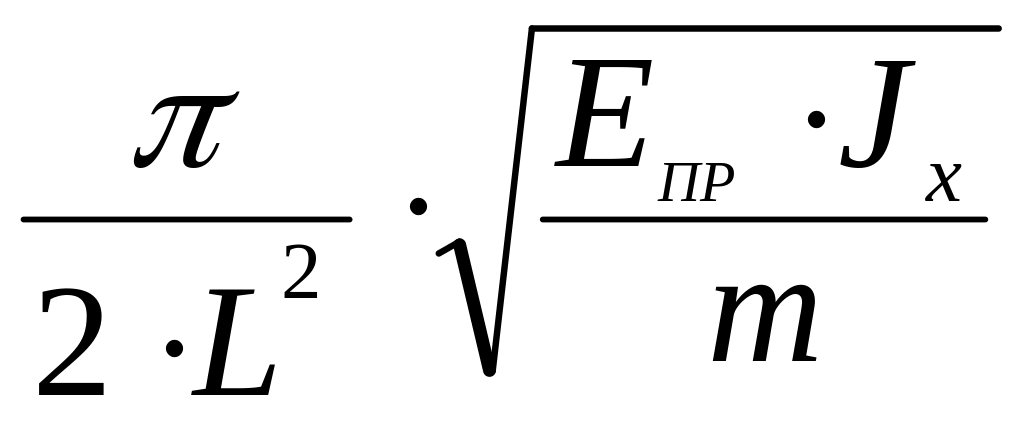
;
где
m – распределенная масса балки; m=·As.
Плотность материала балки:
Приведенный модуль упругости ж/б балки:
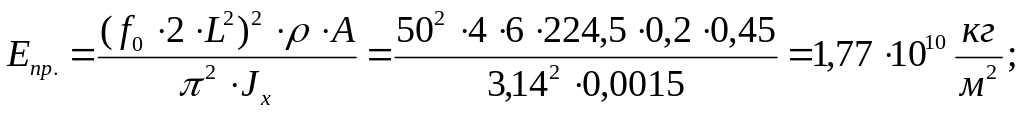
Приведенный модуль упругости ж/б балки равен:
Задача №15
Определить предельный изгибающий момент, соответствующий стадии трещинообразования (Мтр) шарнирно опертой прямоугольной балки. Предельная деформация растяжения бетона р=2·10-4, пролет балки L=6м, высота сечения h=0,4м, погонный вес q=190кг/м. Собственная частота первой формы колебаний балки f0=35Гц. Считать (ЕJ)ст=(EJ)дин.
Решение:
Изгибающий момент трещинообразования в ж/б шарнирно опертой балке может быть определен по формуле:
Задача №16
Установить фактическую расчетную схему балки, если известно , что при испытании ее сосредоточенной статической нагрузкой F=150кН, приложенной в середине пролета максимальный прогиб составил у=0,021м, а при динамических испытаниях собственная частота колебаний балки f0=20Гц. Пролет балки L=6м, погонный вес q=150 кг/м. Считать (ЕJ)СТ=(EJ)Д.
Решение:
Предполагая шарнирное опирание балки определим значение динамической жесткости балки по формуле:
Найдем
также значение статической жесткости
балки по формуле:
Так как полученные значения жесткости (ЕJ)СТ и (EJ)Д для принятого шарнирного опирания балки практически одинаковы, то следовательно фактическое опирание балки является шарнирным.
Задача №17
Определить усилие натяжения и напряжения стальной арматуры длиной L=3м, диаметром d=4мм, если частоты собственных колебаний арматуры соответственно равны: f0(1)=25 Гц ; f0(2)=30Гц.
Решение:
Усилие натяжения арматуры можно определить из выражения:
где m=ρ·А – погонная масса стержня.
Напряжение в арматуре по формуле:
где ρ – плотность материала арматуры (для стали ρ=7,8·103 Нс2/м4);
А – площадь сечения арматурного стержня.
Напряжения в натянутых арматурных стержнях равны:
Усилия натяжения арматурных стержней равны:
Усиление элементов сооружений при реконструкции
Задача №18
Рассчитать
усиление стальной балки перекрытия с
шарнирным опиранием пролетом L=4,5м из
прокатного двутавра №24, запроектированный
под расчетную нагрузку q=20
кН/м в связи с увеличением нагрузки до
qR=40
кН/м, γс=0,9.
В результате проведенного обследования
установлено отсутствие сплошных
коррозионных повреждений, расчетное
сопротивление стали Ry=200
МПа. Усиление производить четырьмя
равнополочными уголками. Предельный
прогиб
Решение:
Условие прочности балки:
Здесь момент инерции сечения усиленной балки равен:
Момент инерции двутарва №24 равен:
Изгибающий момент Мх:
Условие жесткости балки:
Требуемый момент инерции усиленного сечения из условия прочности балки равен:
.
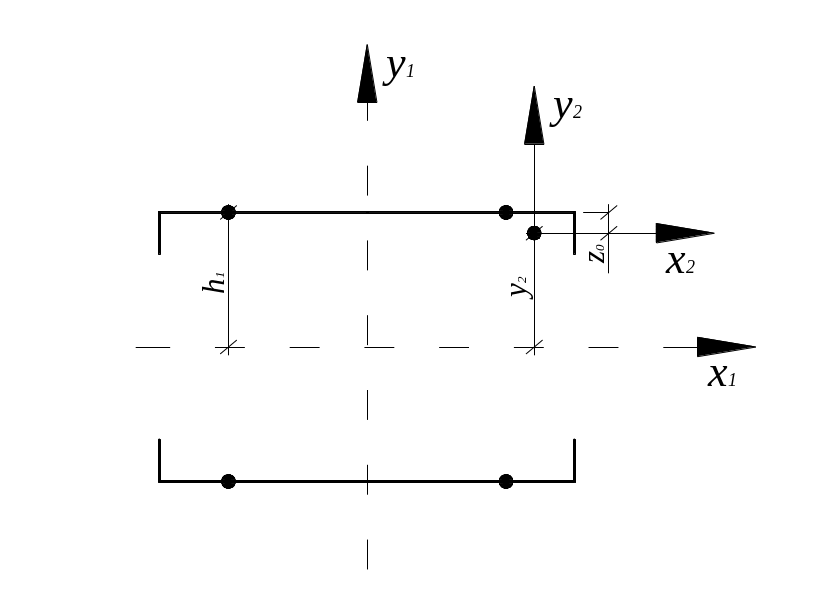
Последовательным подбором значений JX2, y2, A2 выбираем равнополочный уголок L70×70×6 для которого Jx2=37,6см4, z02=1,94 см, A2=8,15см2.
Момент инерции сечения Jx равен:
Максимальное значение нормальных напряжений для принятого усиления:
Условие прочности балки выполнено:
Условие жесткости балки:
Предельное допустимое перемещение:
.
Условие жесткости балки выполнено.
Задача №19
Рассчитать усиление стальной балки монорельса пролетом L=9м выполненного из прокатного двутавра №40, для нагрузки FR=95кН, γс=0,9. Результат проведенного обследования установлено отсутсвие сплошных коррозионных повреждений. Расчетное сопротивление стали Ry=200МПа. Усиление проводить полосовой сталью.
;
Решение:
Условие прочности монорельсовой балки:
Здесь Мх – изгибающий момент:
Требуемый момент инерции сечения балки из условия прочности:
где h – высота сечения.
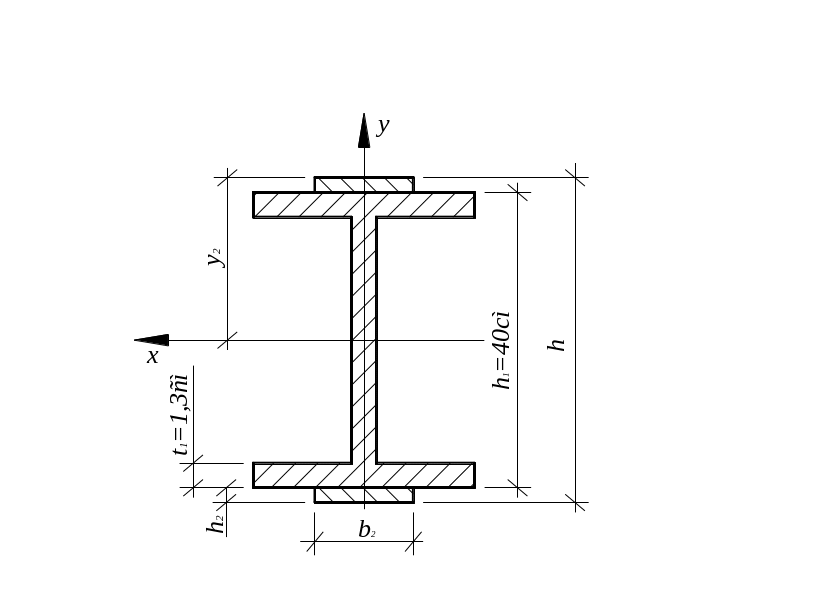
Момент инерции сечения усиленной балки:
где Jx1 – осевой момент инерции двутавра №40;
Jx1=18930см4;
b2 – ширина полосы усиления;
h2 – высота полосы усиления;
y2 – расстояние от оси х до центра тяжести полосы:
Высота сечения h=h1+2h2;
Примем высоту полосы усиления h2=1,0см;
Тогда ширину полосы b2 можно найти из условия:
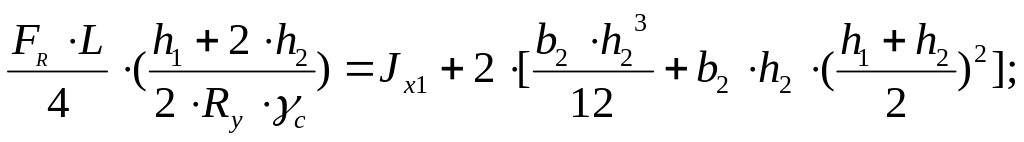
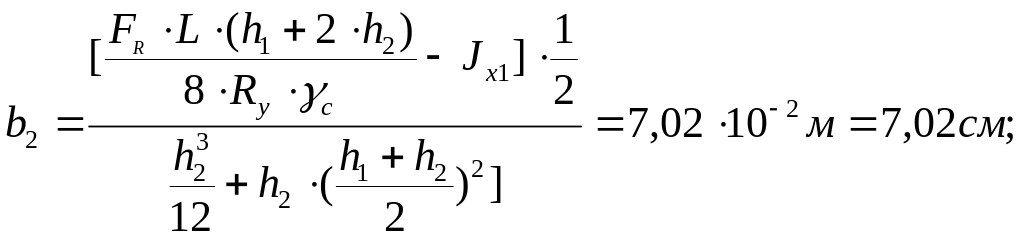
Принимаем b2=8см,
h2=1см.
Определяем момент инерции усиленного сечения монорельса:
Проверяем условие прочности монорельса:
Условие прочности балки выполнено:
Проверяем условие жесткости монорельса.
Максимальный прогиб монорельса:
Предельно допустимый прогиб:
.
Условие жесткости балки выполнено.