АЛГЕБРА ТА ПОЧАТКИ АНАЛІЗУ
І. Перетворення виразів.
І.1. Дійсні числа. Модуль числа. Відсотки. Ціла та дробова частини числа.
Числа, що використовуються при лічбі називаються натуральними (N).
Найбільший спільний дільник декількох натуральних чисел (НСД) – це найбільше число, на яке вони діляться націло.
Найменше спільне кратне (НСК) декількох натуральних чисел – це найменше число, яке на них ділиться націло.
Число називається простим, якщо воно має тільки два дільники: 1 і саме число.
Числа, які мають більш як два дільники називаються складеними.
Два числа називаються взаємно простими, якщо в них один спільний дільник – 1.
Натуральне число ділиться націло на 2, якщо воно є парними.
Натуральне число ділиться на 3 націло, якщо сума його цифр ділиться на 3.
Натуральне число ділиться на 4 націло, якщо дві останні його цифри складають число, що ділиться на 4.
Натуральне число ділиться на 5 націло, якщо воно закінчуються на 0 або 5.
Натуральне число ділиться на 6 націло, якщо воно діляться і на 3 і на 2.
Натуральні числа діляться на 8 націло, якщо три останні його цифри складають число, що ділиться на 8.
Натуральне число ділиться на 9 націло, якщо сума його цифр ділиться на 9.
Натуральні числа, протилежні до них та число 0 складають множину цілих чисел (Z).
Числа, які можна представити у вигляді звичайного дробу, в якому в чисельнику стоять цілі числа, а в знаменнику натуральні називаються раціональними числами (Q).
Раціональними числами є всі цілі числа, десяткові скінченні дроби та десяткові нескінченні періодичні дроби.
Щоб записати десятковий
нескінченний періодичний дріб у вигляді
звичайного дробу, потрібно скористатися
формулою суми нескінченно спадної
геометричної прогресії.
Десяткові нескінченні неперіодичні дроби називаються ірраціональними (Qі).
Раціональні та ірраціональні числа складають множину дійсних чисел (R).
Середнє арифметичне декількох чисел дорівнює відношенню суми цих чисел до їх кількості.
Відсоток (%) – це сота частина величини чи числа. Одиниця рівна 100%
1 задача на відсотки: щоб знайти значення певної кількості відсотків від числа, потрібно це число поділити на 100 і помножити на дане значення відсотків.
2 задача на відсотки: щоб знайти все число, якщо відомо значення певної кількості його відсотків, потрібно дане значення поділити на кількість відсотків і помножити на 100.
3 задача на відсотки: щобзнайти скільки відсотків складає одне число від шншого (відсоткове відношення двох чисел), потрібно перше число поділити на друге і помножити на 100%.
Формула складних відсотків
-
,
де А0
– початковий вклад,
р
– відсоток вкладу, n
– кількість років, Аn
– кінцева сума.
Модуль числа а називається:
Цілою
частиною числа
називається
таке ціле число, що не перевищує а.
Якщо число а
ціле, то його ціла частина дорівнює
самому числу.
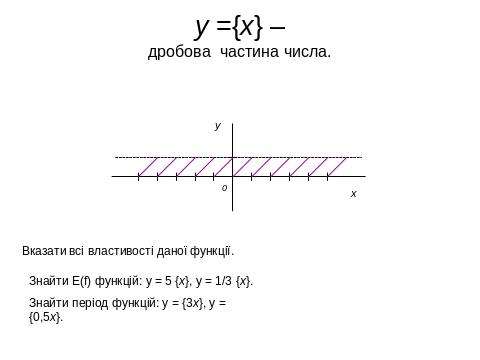
Дробовою
частиною числа
називається
десяткова частина числа. Якщо число а
ціле, то його дробова частина дорівнює
0.
І.2.
Перетворення
алгебрагічних виразів, виразів з
модулями, ,багаточлени, ділення
багаточленів, розкладання
багаточленів на
множники.
В останній формулі х1 та х2 – корені відповідного квадратного рівняння.
Одночленом називається вираз, що містить добутки чисел, невідомих та їх степенів.
Степенем одночлена називається сума степенів змінних, що в нього входять.
Стандартний вигляд має той одночлен, в якому виконані дії множення, на першому місці стоїть числовий множник, а далі змінні в порядку спадання степенів.
Багаточленом називається вираз, що складається з суми одночленів.
Степенем багаточлена називається найбільший із степенів одночленів, що в нього входять.
Щоб помножити одночлен на багаточлен, потрібно його помножити на кожен з доданків багаточлена.
Щоб помножити багаточлен на багаточлен, потрібно кожен член першого багаточлена помножити на кожен член другого з врахуванням знаків одночленів.
Винесення за дужки спільного множника є операцією ділення кожного з доданків на даний множник.
Способи розкладання багаточленів на множники: за допомогою формул скороченого множення, винесення за дужки, групування, використання формули розкладання квадратного тричлена на лінійні множники, ділення багаточленів*(ділення багаточленів виконується так само як і ділення чисел) , використання наслідка з теореми Безу (якщо нулем багаточлена є ціле число а -корінь відповідного рівняння, то його потрібно шукати серед дільників вільного члена і тоді багаточлен націло поділиться на двочлен (х-а)).
Спільний множник, що містить степінь виразу виноситься за дужки з найменшим показником.
Винесення спільного множника за дужки означає операцію ділення кожного доданка на цей множник.
Щоб звести дробові вирази до спільного знаменника, потрібно:
за можливістю розкласти знаменники на множники;
знайти спільний знаменник (всі різні множники з найбільшим показником по одному разу),
знайти додаткові множники до кожного дробу (результат ділення спільного знаменника на кожен із знаменників),
до множити кожен з чисельників на свій додатковий множник та виконати дію між чисельникам и під спільною рискою дробу.
Щоб спростити вираз, в якому є декілька модулів, потрібно:
знайти значення змінної, при якому модулі рівні 0;
нанести ці значення на числову пряму (вони розбивають її на проміжки);
підставляючи будь-яке число з даних проміжків у вирази під модулями, визначаємо їхні знаки на кожному проміжку;
розкриваємо модулі за відповідними знаками на кожному з проміжків, кінцеві результати яких є відповіддю при певному значенні змінної.
І. 3. Перетворення виразів зі степенями.
a0=1;
a1=a;
anam=an+m;
an:am=an-m
(an)m=anm;
(ab)n=anbn ;
(a:b)n=an:bn;
;
;
І. 4. Перетворення виразів з радикалами.
І.5. Перетворення тригонометричних виразів.
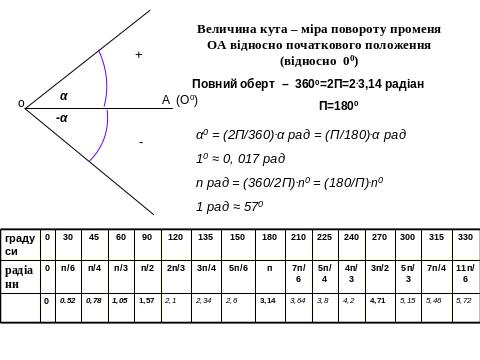
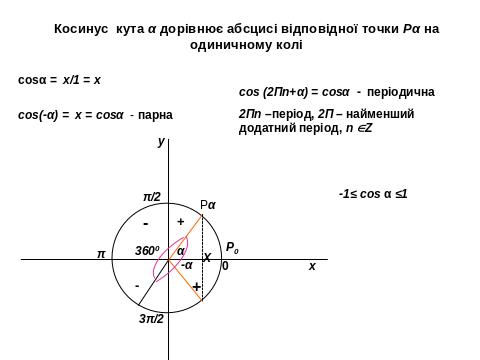
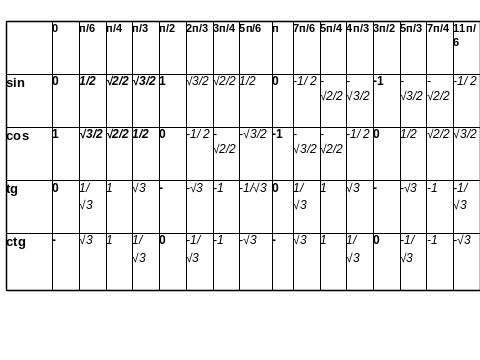
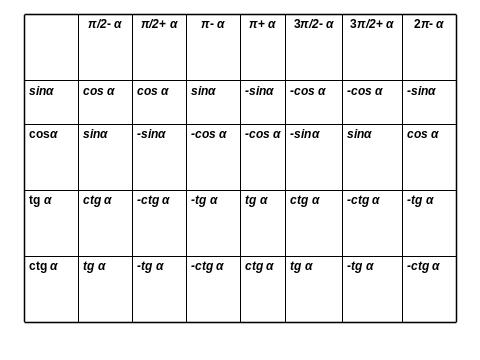
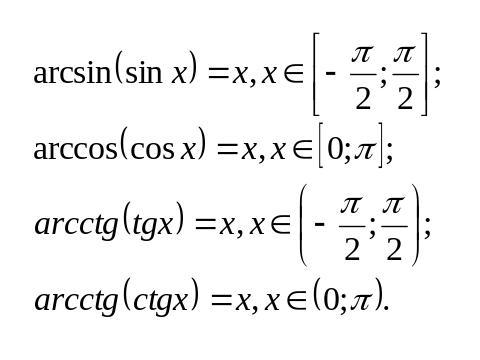
І. 6. Перетворення логарифмічних виразів.
,
ac=b.
a>0,
b>0,
a≠1.
- основна логарифмічна
тотожність.
;
;
;
;
;
;
;
;
;
-
десятковий логарифм;
- натуральний логарифм.
ІІ. Розвязування рівнянь та систем рівнянь.
1. Які з тверджень ведуть до рівносильних перетворень, які розширюють ОВ, які звужують ОВ?
Перенесення членів з однієї частини рівняння до другої зі зміною їх знаків на протилежні;
Зведення подібних доданків;
Зведення дробових членів до спільного знаменника;
Піднесення до непарного степеня обох частин рівняння, якщо вони не містять суму чи різницю виразів;
Добування кореня з непарним показником;
Піднесення до парного степеня обох частин рівняння, якщо ці частини невід ємні в ОВ рівняння;
Додавання до обох частин рівняння довільного виразу, визначеного для всіх х з ОВ;
Множення і ділення обох частин рівняння на довільний вираз, при умові, що він не дорівнює 0 і визначений для всіх х з ОВ.
Піднесення до парного степеня обох частин рівнянь;
Взаємне скорочення подібних членів рівняння ( f(x) - f(x) = 0 ), які не мають смислу при деяких значеннях невідомого;
Відкидання знаменника;
Скорочення дробів в одній частині ( або обох ) рівняння ( f(x) / f(x) = 1);
Множення обох частин рівняння на вираз, який дорівнює 0 при деяких значеннях невідомого, що належить області визначення рівняння;
Додавання (або віднімання) до обох частин рівняння виразу, який не має смислу для деяких значень невідомої з ОВ рівняння;
Скорочення обох частин рівняння на спільний множник, що містить невідоме;
Ділення обох частин на вираз, який дорівнює нулю при деяких значеннях невідомого з ОВ рівняння;
Добування кореня парного степеня з обох частин рівняння;
Множення обох частин рівняння на вираз, невизначений для деяких значень невідомої з ОВ рівняння;
ІІ.1. Розв’язування лінійних, дробово-раціональних, квадратних рівнянь, рівнянь з модулями, систем лінійних та нелінійних рівнянь.
Лінійні рівняння
Випадки 1та 2 для лінйних рівнянь з параметрами.
Квадратні рівняння
Випадок 1 для квадратних рівнянь з параметром, які при цьому зведуться до лінійних (див. вище).
Неповні квадратні рівняння
.
Теорема Вієта
Рівняння зі змінною під знаком модуля.
розкриттям модулів на
проміжках.
Зауваження: всі рівняння розв’язуються на ОДЗ виразів, що входять в дане рівняння.
Системи лінійних рівнянь
Системи нелінійних рівнянь розв’язуються за допомогою підстановок, додавання, симетричні та однорідні системи.
Симетричні системи.
Системи рівнянь виду
де
є симетричними багаточленами (тобто
багаточленами, які не змінюються при
заміні х
на у;
у на
х),
називаються симетричною системою
рівнянь.
Будь-який симетричний багаточлен двох
змінних Р(х;у) може бути записаний
у вигляді багаточлена від основних
симетричних багаточленів
;
.
Зокрема
;
Однорідні системи.
Системи двох рівнянь з двома змінними виду
називаються однорідною (ліві частини кожного з рівнянь - однорідні багаточлени від двох змінних)
Однорідні системи розв’язуються комбінацією двох методів: лінійного перетворення і введення нових змінних.
ІІ. 3. Розв’язування ірраціональних рівнянь
.
.
.
.
Основні методи розв’язування:
Рівняння типу
шляхом заміни кореня більшого степеня
зводяться до квадратного.
Рівняння типу
розв’язується піднесенням
до квадрату лівої та правої частини
(двічі) на ОДЗ.
Однорідне рівняння другого
степеня
розв’язується діленням
на один з доданків та заміною.
Рівняння типу
піднесення
до кубу за формулою (х+у)3=х3+у3+3ху(х+у)
з обов’язковою
перевіркою.
Зауваження: при розв’язуванні будь-яким методом ірраціональні рівняння слід завжди враховувати ОДЗ змінних, які в нього входять та накладати певні умови при нерівносильних перетвореннях або в кінці робити первірку, що не завжди просто.
ІІ. 4. Розв’язування тригонометричних рівнянь.
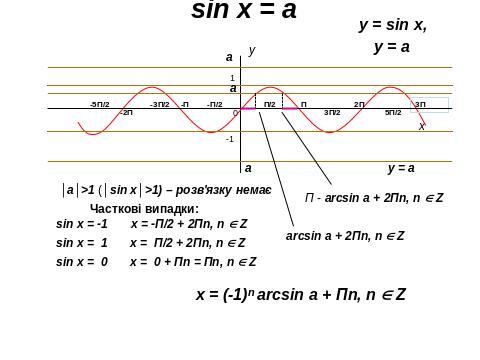
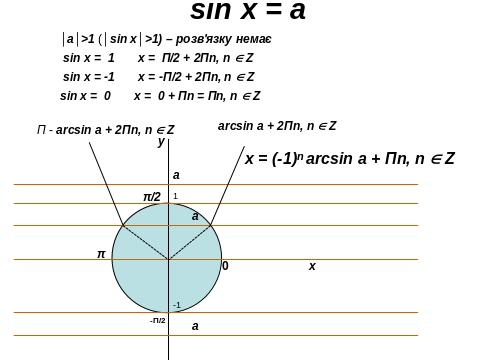
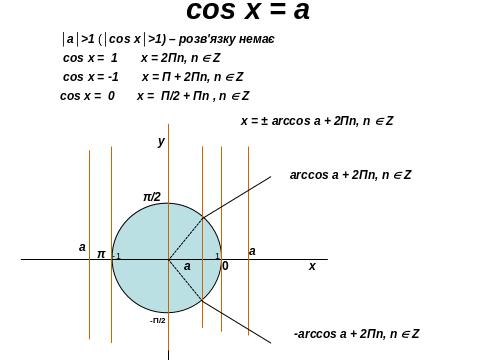
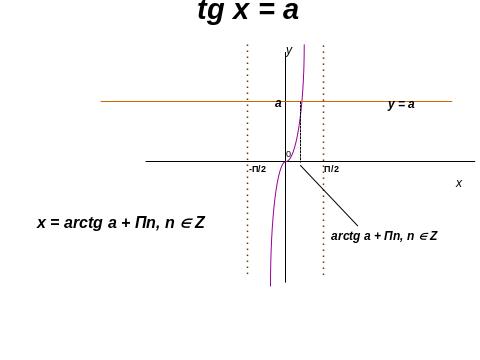
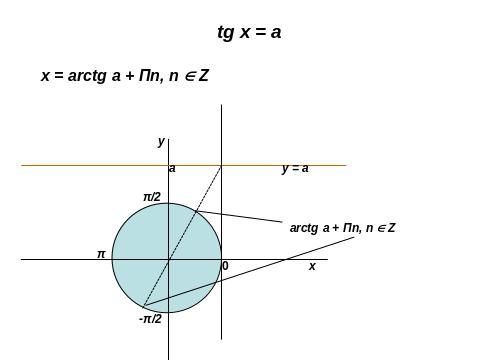
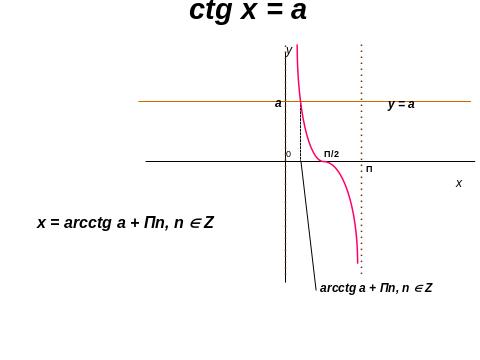
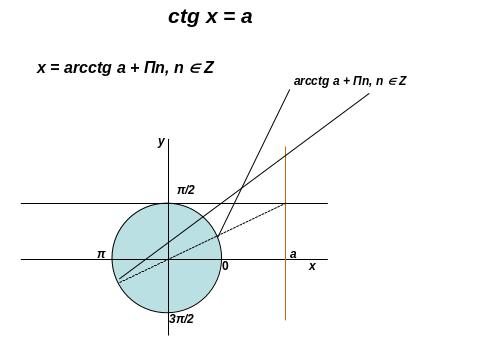
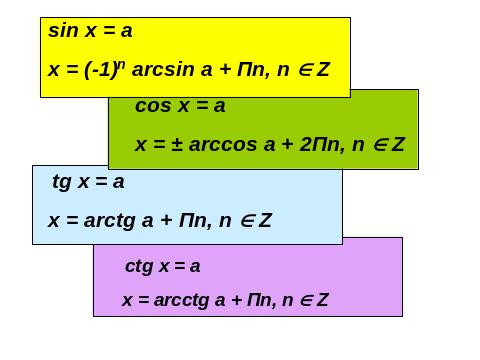
ІІ.5. Розв’язування показникових рівнянь.
1
.
Рівняння виду ax
= b
називається найпростішим (a
0, a
1).
Якщо b 0, то рівняння має єдиний розв'язок x = logab. Якщо b 0, то рівняння розв'язку не має.
2. Показникові рівняння виду af(x) = b, де a 0, a 1, заміною f(x) на t зведеться до попереднього вигляду (1).
3. Показникове рівняння виду af1(x) = bf2(x), де a 0, a 1, b 0, b 1, a f1(x), f2(x) - задані елементарні функції логарифмуванням зведеться до вигляду
f1(x) log ca = f2(x) log cb. Якщо a = b, то рівняння зводиться до f1(x) = f2(x).
4. Показникові рівняння виду F(af(x)) =0, де F(t) і f(x) - задані алгебраїчні функції відносно змінних t і x , заміною af(x) = t спочатку зводиться до рівняння
F(t) = 0, а потім до сукупності рівнянь af(x) = t1, af(x) = t2, af(x) = tn, де t1, tn - корені рівняння F(t) = 0.
5. Рівняння виду ((x))f1(x) = ((x))f2(x) (показниково-степеневі) зводяться до розв'язку слідуючих чотирьох:
1) (x) = -1. Корені цього рівняння є коренями даного, якщо значення функції f1(x) і f2(x) від цих коренів - цілі числа однакової парності або дробові нескоротні з непарними знаменниками і однакової парності чисельники.
2) (x) = 0. Корені цього рівняння являються коренями даного, якщо значення функції f1(x) і f2(x) від цих коренів додатні.
3) (x) = 1. Корені цього рівняння являються коренями даного, якщо існують функції f1(x) і f2(x) від цих коренів.
4) f1(x) = f2(x). Корені цього рівняння являються коренями даного , якщо при значеннях x, що дорівнюють цим кореням, дане рівняння має смисл (зміст).
6. Використання монотонності
Часто при розв'язуванні показникових рівнянь користуються такою теоремою:
Т.1. Для монотонної функції f(x) на інтервалі (a ; b) рівняння f(x) = c, c - стала величина, має не більш одного кореня.
Т.2. Якщо f(x), (x) на (a ; b) є монотонними функціями різного характеру, то f(x) = (x ) має на (a ; b) не більше одного кореня.
ІІ.6. Розв’язування логарифмічних рівнянь
;
Рівняння типу
розв’язується
логарифмуванням за зручною нам основою.
ІІІ. Розвязування нерівностей та систем нерівностей.
ІІІ.1. Розв’язування лінійних нерівностей, нерівностей з модулями, доведення нерівностей.
При розв’язанні нерівностей користуються такими властивостями та методами:
.
.
.
.
.
.
.
Розв’язком системи нерівностей
є
перетин (спільні розв’язки)
множин розв’язків кожної з нерівностей.
Розв’язком сукупності
нерівностей
є
об’єднання (всі розв’язки) множин
розв’язків кожної з нерівностей.
якщо а >0.
якщо а <0.
якщо а <0.
.
.*
.
ІІІ. 2. Розв’язування нерівностей методом інтервалів, дробово-раціональних та, квадратичних нерівностей.
Більшість цих нерівностей розв’язується метордом інтерівалів, суть якого полягає в слідуючому.
Якщо нерівність містить лінійні множники з додатними коефіцієнтами, то наносимо на числову пряму нулі кожного множника і починаючи справа розставляємо знаки «+» «-» і дак далі.
Якщо нерівність містить множники з від’ємними коефіцієнтами при невідомих, то винісши за дужки знак «-» і поділивши на -1 ліву та праву частину нерівності приходимо до поперднього типу.
Якщо маємо строгу дробову нерівність з лінійними множниками, то розв’язуємо як у першому випадку.
Якщо дробова нерівність нестрога, то нулі чисельника включаємо, а нулі знаменника виколюємо.
Якщо деякі лінійні множники в строгій нерівності стоять в парній степені, то розбиваючи на проміжки, їх пропускаємо, а далі діємо так само.
Якщо ж нерівність нестрога, то поступаємо аналогічно, але до відповіді додаємо всі нулі цих множників, якщо вони туди не ввійшли.
Якщо чисельник і знаменник дробу містять різнойменні функції, то на їхній ОДЗ знаходимо нулі чисельника та знаменника і поступаємо як у звичайному методі інтервалів, звертаючи увагу на той факт, що деякі нулі можуть зустрічатися декілька разів (дивись метод інтервалів при парних степенях множників) та нерівність може містити модуль (знак модуля і квадрата однаковий).
Квадратичну нерівність або зводимо до методу інтервалів, розкладаючи квадратний тричлен на лінійні множники за відомою формулою, або за допомогою графіка функції. (Дивись тему функції).
ІІІ. 3. Розв’язування ірраціональних нерівностей .
якщо а>0.
якщо а≥0.
якщо а>0 або
якщо а≤0 .
ІІІ. 4. Розв’язування тригонометричних нерівностей
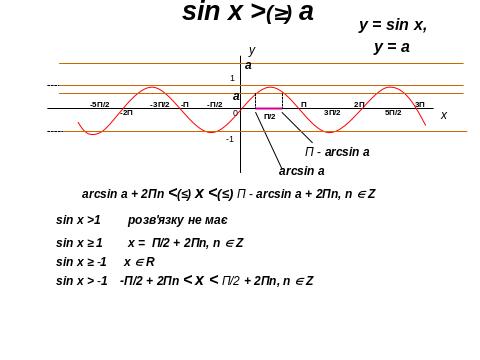
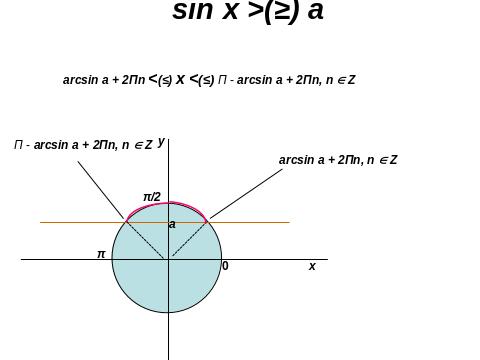
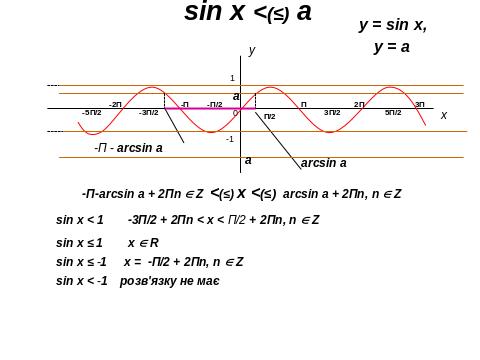
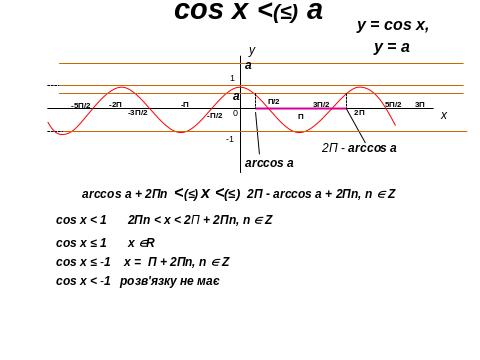
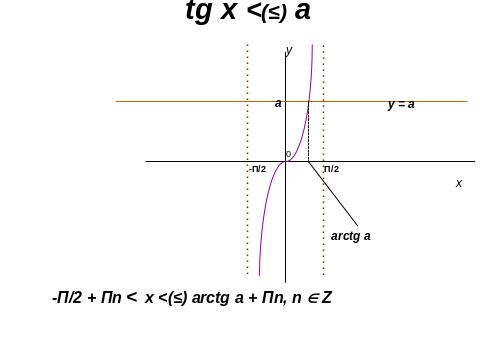
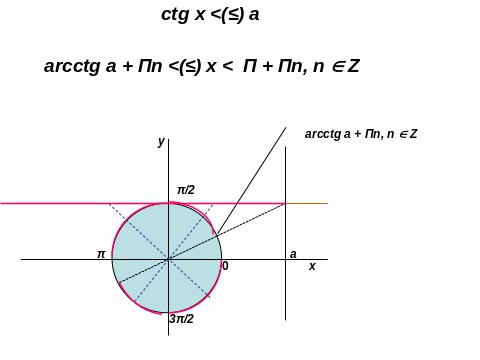
ІІІ. 5. Розв’язування показникових нерівностей
ІІІ. 6. Розв’язування логарифмічних нерівностей
IV. Функції.
IV. 1. Властивості, графіки функцій, основні функції.
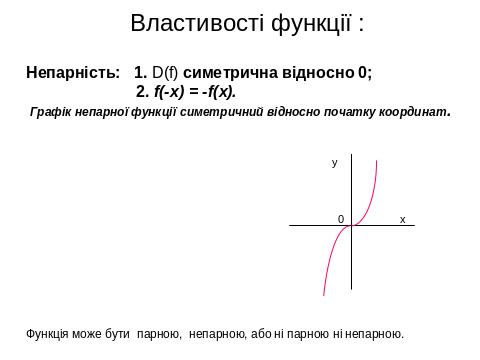
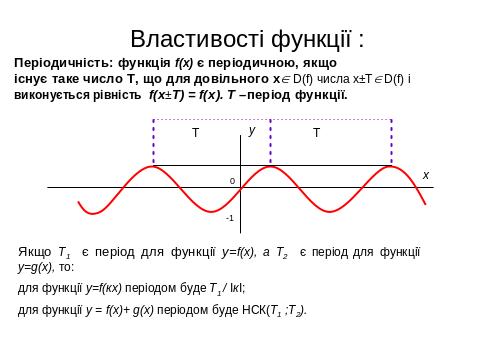
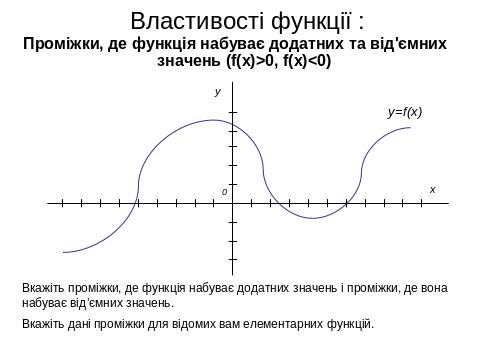
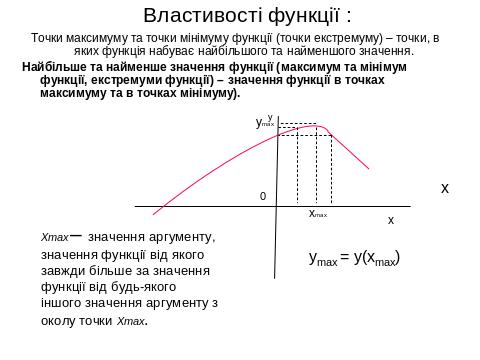
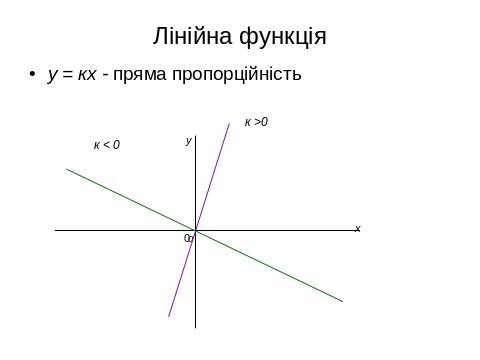
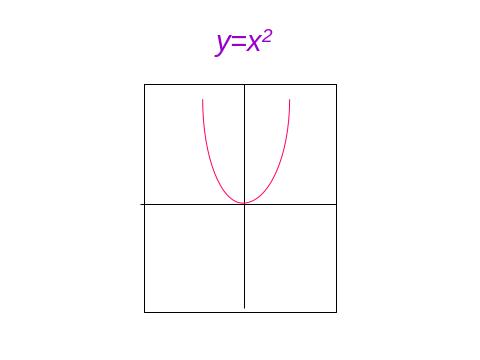
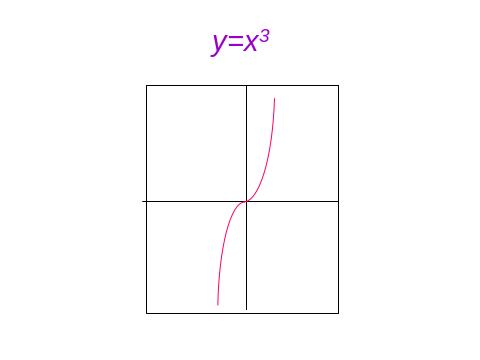
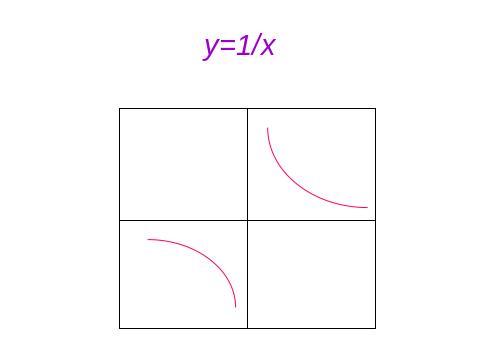
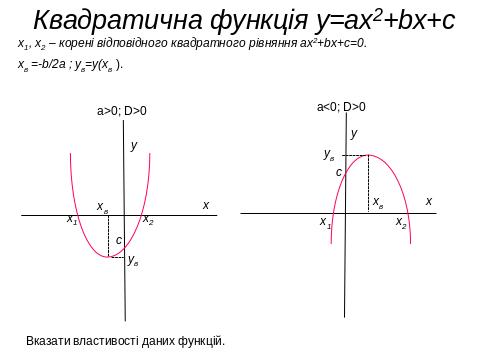
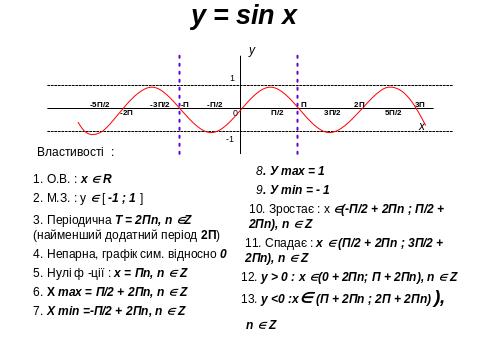
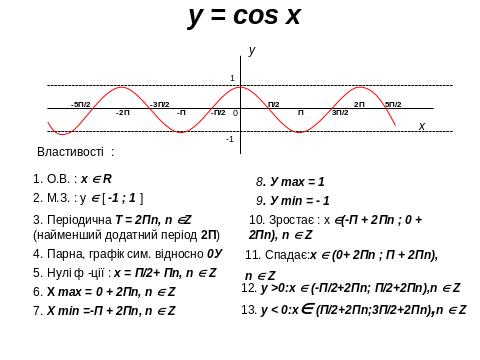
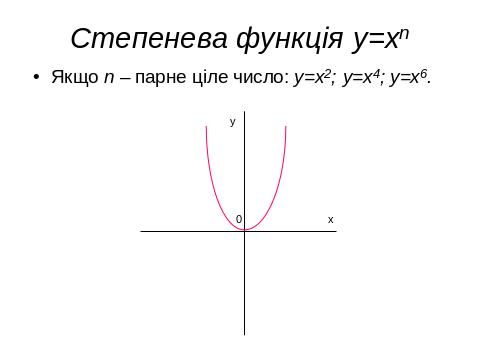
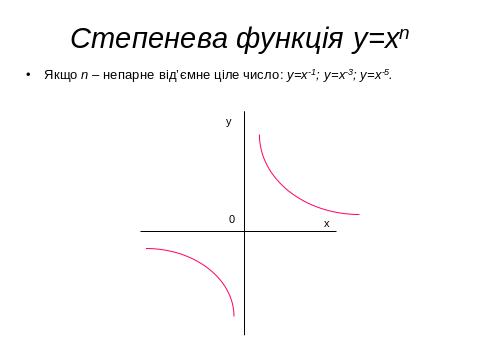
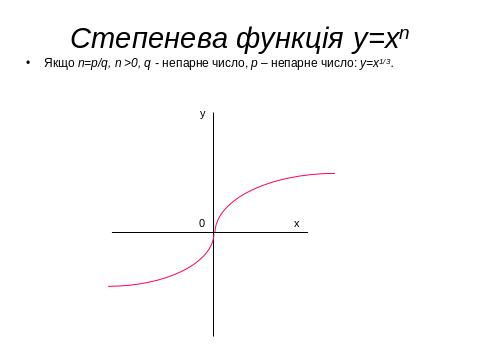
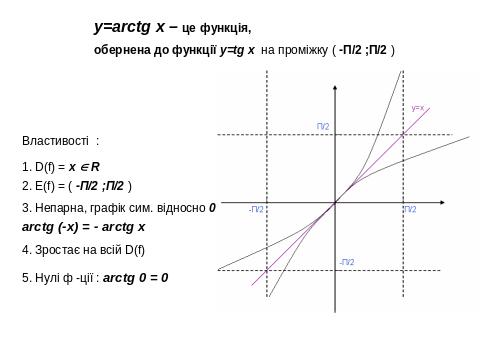
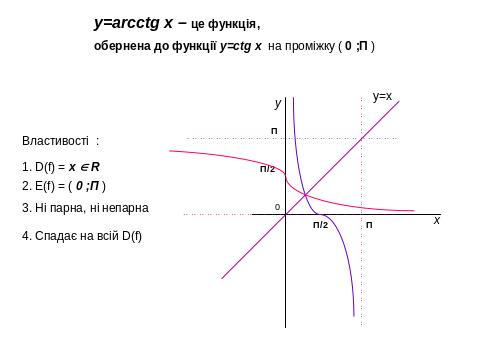
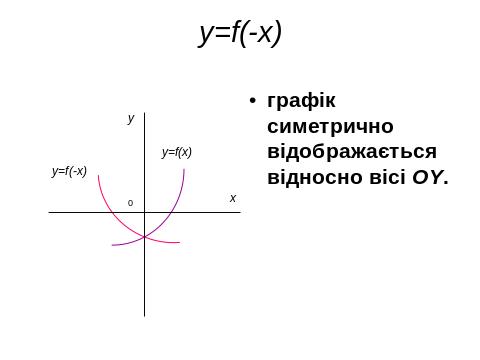
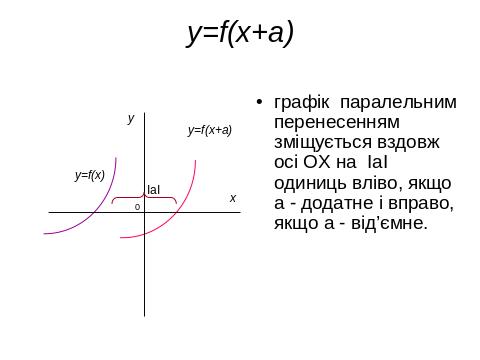
IV. 2. Геометричні перетворення графіків функцій , побудова ГМТ.
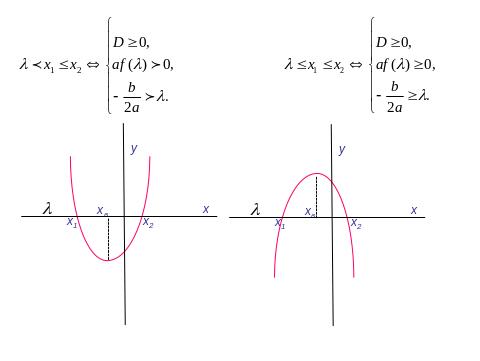
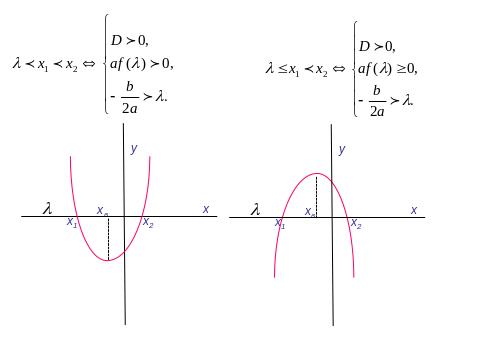
IV.3. *Розташування коренів квадратного рівняння.
Розв’язування вправ з параметром за допомогою графіків .
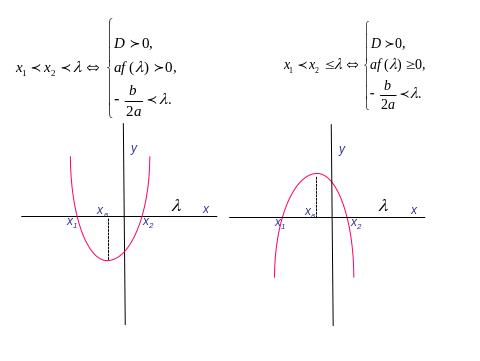
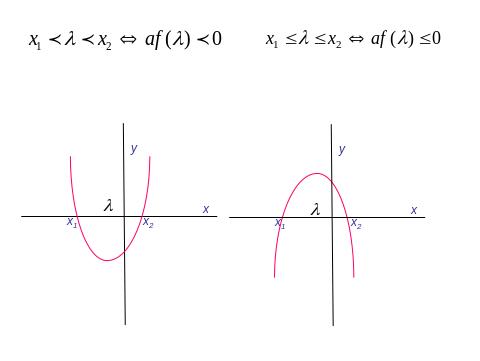
IV. 4. Розв’язування рівнянь та нерівностей з використанням властивостей функцій.
Не завжди при роязв’язуванні певного типу завдань спрацьовують основні методи розв’язування. При розв’язуванні деяких рівнянь та нерівностей, які містять різнойменні функції, доцільно оцінювати ліву та праву частини рівняння чи нерівності. Як правило, ті значення змінної при яких одна частина рівняння має певне найменше значення, інша – таке ж саме найбільше. Отже, дане значення змінної і є розв’язком рівняння чи нерівності.
V. Прогресії, відсотки, текстові задачі.
1. Послідовність чисел
називається
арифметичною прогресією,
якщо кожен її член, починаючи з другого,
дорівнює попередньому, складеному з
одним і тим же числом, яке називається
різницею прогресії:
.
Загальний член арифметичної
прогресії:
Властивості членів арифметичної
прогресії:
;
Формули суми n
перших членів арифметичної прогресії:
;
.
Послідовінсть чисел
називається
геометричною прогресією,
якщо перший її член, відмінний від нуля,
а кожен наступний, починаючи з другого,
дорівнює попередньому, помноженому на
одне і ти ж числ, відмінне від нуля, яке
називається знаменником прогресії:
.
Загальний член геометричної
прогресії:
Властивості членів геометричної
прогресії:
;
Формула суми n
перших членів геометричної прогресії:;
.
Формули добутку n
перших членів геометричної прогресії:
;
.
Сума членів нескінченно
спадної геометричної прогресії
,
.
2. У задачах на спільну роботу
використовують величини: об’єм
всієї роботи А (часто позначають через
1), час t,
продуктивність праці
.
3. Якщо суміш містить к
різних речовин, маси
яких дорівнюють
,
то масова концентрація і-ої
суміші дорівнює:
.
4. При русі двох тіл назустріч
одне одному зі швидкостями v1
і v2
в різних напрямках, час, за який вони
зустрінуться (при початковій відстані
між ними S)
дорівнює
(
при русі по колу
);
при русі в одному напрямку (v1
> v2)
час, за який перше тіло наздожене друге,
дорівнює
( при русі по колу
).
5. Якщо при діленні натурального
числа А
на натуральне число В
в частці одержуємо q,
а в остачі r
(r<B),
то
Позиційний запис натурального числа в десятковій системі числення
,
.
Vі. Математичний аналіз.
Vі.1. Похідна, інтеграл.
.
Щоб знайти границю функції в точці, потрібно знайти значення функції в даній точці.
Щоб позбутися невизначеностіей
або скорочують чисельник та знаменник
, використовуючи формули скороченого
множення, або домножують чисельник та
знаменник на спряжений множник, або
ділять вирази в чисельнику та знаменнику
на найбільшу степінь змінної.
Похідною функції в точці
називають
.
Похідна
дорівнює кутовому
коефіцієнту дотичної
до графіка функції
в
точці диференціювання
:
- кут нахилу дотичної до додатного
напрямку вісі ОХ, проведенї в точці
дотику.
Кут, який утворює графік функції з віссю ох, дорівнює куту між дотичною до графіка цієї функції, проведеної в точці перетину до вісі ох.
Рівняння дотичної
до графіка функції
в точці
:
.
Механічний зміст
похідної:
,
Таблиця похідних:
Основні правила диференціювання:
Якщо похідна в кожній точці проміжку додатна, то функція на ньому зростає.
Якщо похідна в кожній точці проміжку від’ємна, то функція на ньому спадає.
Внутрішні точки ОВ, в яких похідна дорівнює нулю називаються стаціонарними точками.
Точки, в яких похідна дорівнює нулю або не існує називаються критичними точками.
Якщо при переході через критичну точку похідна функції змінює знак з «+» на «-», то ця точка є точкою максимуму функції.
Якщо при переході через критичну точку похідна функції змінює знак з «-» на «+», то ця точка є точкою мінімуму функції. (точки екстремуму)
Значення функції в критичних точках називається максимумом чи мінімумом функції. (екстремуми функції).
Щоб знайти найбільше та найменше значення функції на відрізку, потрібно знайти значення функції в критичних точках, що належать відрізку та в кінцях відрізка і вибрати з цих значень найменше та найбільше.
Функція F(x) називається первісною функції f(x) на проміжку, якщо F(x) диференційована на ньому і справджується рівність: (F(x))’=f(x).
Невизначеним інтегралом
функції f(x)
називають сукупність
усіх первісних F(x)+С,
С – стала інтегрування:
.
Таблиця основних інтегралів:
Основні правила інтегрування:
Формула Ньютона-Лейбніца:
.
Площа криволінійної трапеції:
