Метод резолюций

Методику продемонстрируем на примере. Пусть требуется доказать:

.

Сначала поступают точно так же, как и по методике Вонга, только необходимо преобразовать клаузу таким образом, чтобы слева от символа  был ноль :

Затем из дизъюнктов составляют резолюции до тех пор, пока не получится ноль.

Выпишем по порядку все посылки и далее начнем их «склеивать». Дизъюнкты можно перебирать автоматически в соответствии с возрастанием порядковых номеров. Такая стратегия поиска нуля очень непродуктивна. К решению данной задачи можно подойти творчески.

В итоге получим:

1. А В	5. (1; 4)
2. С А	6. (2; 4) С
3.	7. (3; 5)
4.	8. (6; 7) 

Иначе, произведенные раннее преобразования, можно представить в следующем виде:

Алгоритм вывода по принципу резолюции:

Шаг 1: принять отрицание заключения, т.е.  В;

Шаг 2: привести все формулы посылок и отрицания заключения к конъюнктивной нормальной форме;

Шаг 3: выписать множество дизъюнктов всех посылок и отрицания заключения: K = {D₁; D₂; . . . D_k };

Шаг 4: выполнить анализ пар множества K по правилу:

“если существуют дизъюнкты D_i и D_j, один из которых (D_i) содержит пропозициональную переменную А, а другой (D_j) - контрарную ей переменную А, то соединить эту пару логи­ческой связкой дизъюнкции (D_i  D_j) и сформировать новый дизъюнкт - резольвенту, исключив контрарные литеры А и А; резольвенту включить в множество К,;

Шаг 5: если в результате соединения дизъюнктов, содержащих контрарные предикаты, будет получена пустая резольвента (пустой дизъюнкт) - , то конец (доказательство подтвердило противоречие), иначе включить резольвенту в множество дизъюнктов K и перейти к шагу 4; по закону идемпотентности любой дизъюнкт и любую резольвенту КНФ можно использовать неоднократно.

Пример: Доказать истинность заключения

(AB); (AB);

(AB).

1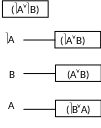 ) (AB) - посылка;

2 ) (AB)=(AB)(BA) - посылка;

3)(AB)=(AB) –отрицание заключения;

4) K = {(AB); (AB); (BA); (AB)};

5) (AB)(AB)= A - резольвента;

6) A(AB)=B - резольвента;

7) B(BA)=A - резольвента;

8) AA=  - пустая резольвента.

A

0

Пример: доказать истинность заключения

(AB)(CD); (DBM); M

(AC).

• (AB)(CD)=(AB)(CD) - посылка;

• DBM=(DB)M=(DBM) - посылка;

• M - посылка;

• (  A  C ) = A C - отрицание заключения;

• множество дизъюнктов:

K ={A; C; M; (AB); (CD); (DBM)};

• A(AB)=B - резольвента;

• множество дизъюнктов:

K ={A; C; M; (AB); (CD); (DBM); B};

• B(DBM)=(DM) - резольвента;

• множество дизъюнктов:

K ={A; C; M; (AB); (CD); (DBM); B; (DM)};

• (DM)(CD)=(CM) - резольвента;

• множество дизъюнктов:

K ={A; C; M; (AB); (CD); (DBM); B; (DM); (CM)};

• ( CM)M=C - резольвента;

• CC= - пустая резольвента.

Так доказана истинность заключения (AC).

Пример: доказать истинность заключения

( ABС ); (CD  M); ( N DM )

ABN.

• ABC=(AB)C=(ABC) – посылка (один дизъюнкт);

• CDM=(CD)M=(CDM) –посылка (один дизъюнкт);

• NDM=(N)DM=( N  D )( N  M ) – посылка (два дизъюнкта);

• ((AB)N)=ABN - отрицание заключения (три однолитерных дизъюнкта);

• множество дизъюнктов:

K={(ABC); (CDM); (ND); (NM); A; B;N};

• (MN)N=М - резольвента;

• множество дизъюнктов:

K₁={(ABC); (CDM); (ND); (NM); A; B; M; N};

• (CDM)M =(CD) - резольвента;

• множество дизъюнктов:

K₂={(ABC); (CDM); (ND); (NM);A; B; M;N; (CD)};

• (ABC)(CD) =(ABD) – резольвента;

• множество дизъюнктов:

K₃={(ABC); (CDM); (ND); (NM); A; B; M; N; (CD); (ABD)};

• (ABD)A=(BD) - резольвента;

• множество дизъюнктов:

K₄={(ABC); (CDM); (ND); (NM); A; B; M; N; D; (CD); (ABD)}; (BD) };

• (BD)B=D - резольвента;

• множество дизъюнктов:

K₅={(ABC); (CDM); (ND); (NM); A; B; M; N; D; (CD); (ABD)}; (BD); D};

• D(ND)=N - резольвента;

• множество дизъюнктов:

K₆={(ABC); (CDM); (ND); (NM);A; B; M; N; D; (CD); (ABD)}; (BD); D}; N};

• N N = - пустая резольвента.

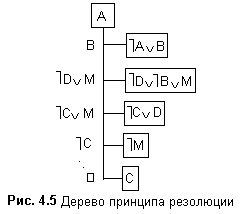
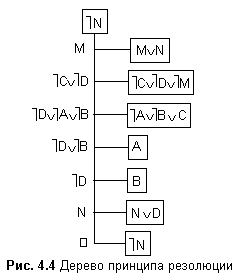
Для демонстрации удобно исполь­зовать граф типа дерево, корнем которого является один из дизъюнктов отрицания заключения, а вершинами – дизъюнкты всех посылок и отрицания заключения. Узлами графа типа дерево являются резольвенты.

Достоинством принципа резолюции является то, что при доказательстве истинности заключения применяют только одно правило: поиск и удаление контрарных литер на множестве дизъюнктов до получения пустой резольвенты.

Алгоритм резолюции основан на том, что выводимость формулы В из множества посылок F₁; F₂; F₃; . . . F_n равносильна доказательству теоремы

(F₁F₂F₃. . .F_nB),

формулу которой можно преобразовать так:

(F₁F₂F₃. . .F_nB) =

((F₁F₂F₃. . .F_n)B) =

(F₁F₂F₃. . .F_n( B)).

Следовательно, заключение В истинно тогда и только тогда, когда формула (F₁F₂F₃...F_n(B))=л. Это возможно при значении “л” хотя бы одной из подформул F_i илиB.

Для анализа этой формулы все подформулы F_i иB должны быть приведены в конъюнктивную нормальную форму и сформировано множество дизъюнктов, на которые распадаются все подформулы. Два дизъюнкта этого множества, содержащие пропозициональные переменные с противоположными знаками (контрарные атомы) формируют третий дизъюнкт - резольвенту, в которой будут исключены контрарные пропозициональные переменные. Неоднократно применяя это правило к множеству дизъюнктов и резольвент, стремятся получить пустой дизъюнкт. Наличие пустого дизъюнкта свидетельствует о выполнении условия F₁F₂F₃...F_nB=л.

12