Метод дедуктивного вывода

Пример: суждение: ”Дан не треугольник (B). Если сумма внутренних углов многоугольника равна 180^о (А), то многоугольник есть треугольник (В). Следовательно, сумма внутренних углов многоугольника не равна 180^о(A)”.

Формула этого суждения (m.t.) имеет вид:

B; AB

A.

Пример. доказать истинность заключения:

(AB); (AC); (BD)

(CD).

• F₁=(AC) - посылка;

• F₂=(AB)(CB) - заключение по F₁ и или правилу 12;

• F₃=(BD) - посылка;

• F₄=(CB)(CD) - заключение по F₃ и правилу 12;

• F₅=(AB)(CD) заключение по F₂ и F₄ и правилу5;

• F₆=(AВ) - посылка;

• F₇=(CD) - заключение по F₅ и F₆ и правилу m. p..

Так доказана истинность (CD).

Процесс дедуктивного вывода удобно проследить на графе, вершинами которого являются формулы, а дугами – отношения

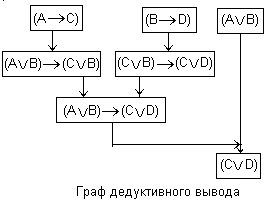
Пример: доказать истинность заключения:

(AB)(CD); ( DBE );  E

C A.

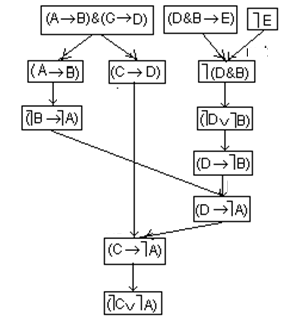
Ниже показан процесс дедуктивного вывода заключения.

• F₁=(DBE) - посылка;

• F₂=E - посылка;

• F₃=(DB) - заключение по F₁ и F₂ и правилу m. t.;

• F₄=(АВ)(СD) - посылка;

• F₅=(AВ) - заключение по F₄ и правилу 7;

• F₆=(СD) - заключение по F₄ и правилу 7;

• F₇=(BA) - заключение по F₅ и правилу 7;

• F₈=(DB) - заключение по F₃ и закону де Моргана;

• F₉=(DB) - заключение по F₈;

• F₁₀=(D A) - заключение по F₇ и F₉ и правилу 5;

• F₁₁=(С A) - заключение по F₆ и F₁₀ и правилу 5;

• F₁₂=(С A) - заключение по F_II .

Метод Вонга

Пусть дана клауза в своей наиболее общей форме:

В₁, В₂, …, В_n  А₁, А₂, …,A_n

Шаг 1. Снятие отрицаний с посылок и заключений. С этой целью нужно опустить знак отрицаний у A_i и B_j и перенести их в противоположные стороны относительно символа .

Шаг 2. Если слева от символа  встречается конъюнкция, а справа дизъюнкция, то их следует заменить на запятые.

Шаг 3. Если после предыдущих шагов оказалось, что связкой, расположенной слева от , является дизъюнкция, а справа – конъюнкция, то образуются две новые клаузы, каждая из которых содержит одну из двух подформул, заменяющих исходную клаузу.

Шаг 4. Если одна и та же буква находится с обеих сторон символа, то такая строка считается доказанной. Исходная клауза является теоремой, если все ветви оканчиваются истинными клаузами. В противном случае переходим к шагу 3.

Пример.

Выяснить, является ли клауза теоремой:

.

Решение.

Шаг 1. .

Избавляемся от отрицаний. В результате получаем: .

Шаг 2. Поскольку слева от символа  не встречается конъюнкция, а справа не встречается дизъюнкция, то шаг 2 как таковой отсутствует.

Ш аг 3. Построим дерево доказательств (рис. 11):

Так как есть не доказанные строки, то исходная клауза теоремой не является.

Пример.

Выяснить, является ли клауза теоремой:

.

Решение.

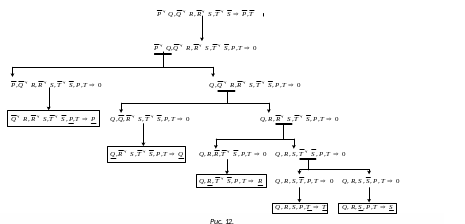
Представим ход доказательства в виде дерева (рис. 12). Поскольку все строки доказаны, то исходная клауза является теоремой.