3 Тұрақтанған қысқа тұйықталу режимі

Электрлі жүйенің спецификалық элементі болып табылатын, синхронды машинаның өтпелі үрдістер теориясы, жоғары қуатты (синхронды генераторлар және ірі электрқозғалтқыштар) синхронды машиналардағы өтпелі үрдістердің өту сипаты, тұтас жүйенің белгілі бір деңгейде әсер ететіндігінен, электрлі жүйелердегі өтпелі үрдістердің жалпы теориясында негізгі орындардың бірін алады.

Асинхронды қозғалтқыштар, электрлі жүйелердің жүктеме тораптарында электр энергиясы тұтынушыларының ішінде басым орнын алады, сонымен қатар электрлі жүйе режимінің өзгеруі кезіндегі, жүктеме тораптарының тәртібін де, берілген тораптардың электрлі тұтыну режимінің өзгерісінің, электрлі жүйенің режиміне әсерін де анықтайды.

Ірі синхронды машиналар мен жүктеме тораптарының тәртіп спецификаларын есепке ала отырғандағы, электрлі жүйелердегі өтпелі үрдістерді зерттеу әдістері, желілі үшфазалы тізбектердегі өтпелі үрдістерді талдау кезінде орын алатын, бұрын қарастырылған әдістен айтарлықтай ерекшеленеді.

Өтпелі үрдістер теориясының көзқарасымен, синхронды және асинхронды машиналардың ұқсастығы мен айырмашылығын қарастырайық. Анықполюсті синхронды машина, ротордың бойлы осіндегі ауалы саңылау көлденең осіндегі саңылаудан айтарлықтай кіші болатындығымен бейімделген, ротордың магниттік симметриялы еместігі салдарынан симметриялы емес болып табылады. Турбогенераторларда (анық емес полюсті машина) симметрия еместіктің бұл түрі жоқ болады, өйткені қабылданған ықтималдықтардың шекарасындағы ауалы саңылау, ротордың бүкіл шеңберінің бойымен тепе тең болады. Анықполюстік және анық емес полюсстік машиналардың электрлі симметрия еместігі, қоздыру орамасы ротордың тек бойлы осімен әрекет ететіндігімен бейімделген. Анықполюсті машинаның демпферлі орамасының бойлы және көлдінең осьтері бойынша әрекеті де әртүрлі болады. Сонымен, синхронды машиналар негізінен симметриялы емес болып табылады.

Ауалы саңылауы тепе тең болатын асинхронды машиналар, магниттік жүйесі бойынша да, ротор мен статор орамалары бойынша да симметриялы болып табылады. Асинхронды машиналардың құрылымы синхрондылардан айтарлықтай ерекшеленеді, негізінен бұл айырмашылық осы машиналардың роторлары құрылымдарының әртүрлілігімен бейімделеді. Асинхронды машина роторының орамасы симметриялы болады және түйіспелі сақиналы машиналар үшін, ротордың фазалар саны негізінен статордың фазалар санына тең болады. Қысқа тұйықталған роторлы машиналарда, ротордың фазалар саны, оның ойықтарының санына және машинаның полюстер жұбының санына тәуелді болады. Асинхронды машинаның жылдамдығы жүктемеге тәуелді болады, яғни тұрақты айналым жылдамдығындағы қалыпты жағдайда жұмыс істейтін синхронды машинаға қарағанда айнымалы болып табылады.

Сонымен, синхронды және асинхронды машиналар, жүктеменің өзгеруі кезіндегі айналым жылдамдығы бойынша, электрлік және магниттік симметрияның бар болуына қатысты, негізгі элементтер мен орамаларының құрылымы бойыынша өзгешеленеді.

Синхронды және асинхронды машиналардың жалпылығы, олардың барлығы электромагниттік индукция заңын пайдалануға негізделгендігімен бейімделген, барлық электрлі машиналар үшін қайтымдылық принципі қолданылады. Тұрақтанған режимде, синхронды және асинхронды машиналарда, ауалы саңылауында, бірдей синхронды жылдамдықпен қозғалатын статор мен ротордың магниттік ағынының, магниттелген күш толқындары құрылады.

Кеңістікте айналатын магниттелген күштер және магнит ағыны көп фазалы да, екі фазалы да орамалармен туылатыны белгілі. Осының салдарынан Горев-Парк теориясы бойынша машиналарды түрлендіру кезінде қолданылатын, қарастырылған машиналардың статоры мен роторының көпфазалы орамаларын екіфазалымен ауыстыру мүмкіндігі туылады.

Бірқатар қысқартуларды енгізу және айнымалы тоқты нақты машиналарды идеалдау, белгілі бір жалпыланған машинаны қарастыруға мүмкіндік береді, оның жеке жағдайы синхронды немесе асинхронды машина болып табылады. Осыдан машиналардың екі түрінде де өтпелі үрдістерді талдау үшін қолдануға болатын жалпы дифференциалды теңдеулерді құруға мүмкіндік туылады.

Жоғарыда айтылған синхронды және асинхронды машиналардың айырмашылықтары, олардың аналитикалық зерттеулерінде белгілі бір түрде көрінетінін атап өтейік.

Келешекте математикалық моделдеудің негізгі объектісі ретінде, анық полюсті роторы бар, «идеалданған» деп аталатын синхронды машина қарастырылады. Шынайы машиналарды идеалдау қажеттілігі, өтпелі үрдістердің аналитикалық талдауына бағытталуымен бейімделген, бұған келесі себептер қиыншылық тудырады: ауалы саңылауда магниттік қозғалыс күші күрделі үлестірілген және үздіксіз өзгереді, осының салдарынан жоғары гармоникалар және т.б. пайда болады. Аталған факторларды есепке алу сызықты емес дифференциалды теңдеулердің өте үлкен жүйелеріне келтіреді, олардың талдауы осы оқу құралының шегінен асып кетеді.

Аналитикалық зерттеулердің жеткілікті жоғары дәлдігін қамтамасыз ететін, синхронды машиналардың өтпелі үрдістер теңдеулері, шамамен бір уақытта А.А.Горев /1/ және Р.Парк /2/ ғалымдарымен ұсынылған. Олардың зерттеу объектісі ретінде қарастырған идеалданған синхронды машина, ықтимал ретінде қабылданатын келесі ерекшеліктермен сипатталады:

- машинаның магниттік тізбегі қанықпаған болып қабылданады, яғни болаттың магниттік өтімділігі ;

- статордың фазалы орамалары симметриялы боып табылады;

- кеңістіктегі үлестірілген магниттік қозғаушы күштері және индукциясы синусоидалды болып қабылданады;

- орамалардың сейілу индуктивтіліктері ротордың қалпына тәуелді емес болып қабылданады.

Идеалданған анық полюсті синхронды машинаның сұлбалы көрінісі 3.1 суретте келтірілген. Статордың фазалы орамаларының симметриялығы жөнінде ықтималдығы бойынша (ораманың басы «Н» индексімен, ал соңы «К» индексімен белгәленген), олардың А, В және С магниттік осьтері симметриялы үшсәулелі жұлдызды көрсетеді. Машинаның роторы анық полюстіктің нәтижесінде екі симметрия осіне ие болады: бойлы және көлденең . Ротордың бойлы осінің оң бағыты ретінде, бойымен тұрақты тоқ жүріп өтетін, қоздыру орамасымен тудырылатын, магниттік ағынның оң бағытымен сәйкес келетін бағытты қабылдаймыз; ротордың көлдінең осінің оң бағыты ретінде, осінің оң бағытынан қалып тұратын бағытты қабылдаймыз. Машинаның роторында екі қысқа тұйықталған демпферлі орамалар орналасқан бойлы (индекс «rd») және көлденең (индекс «r ») демпферлі контурлар.

Синхронды машинаның статорлы және роторлы контурларының ағындар берілісінің теңдеулерін қарастырайық. Машина болатының қанықпағандығы жөнінде ықтималдықтың негізінде, оның орамаларының ағын берілістері статордың және ротордың тоқтарының сызықты функциялары болыып табылады.

а) статордың фазалы орамаларының ағын берілісі теңдеулері

(1.14)

немесе матрицалы түрінде

(1.15)

мұндағы

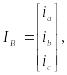
(1.16)

(1.17)

б) ротор орамаларының ағын берілістер теңдеулері (қоздыру, бойлы және көлденең демпферлі контурларының)

(1.18)

немесе матрицалы түрде

(1.19)

мұндағы

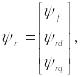
(1.20)

Матрицаларды біріктіруді қолдана отырып, синхронды машинаның ағын берілістерінің толық матрицалы теңдеуін жазамыз

(1.21)

Статордың фазалы орамаларының өзіндік индукция коэффизиенттері айнымалы сипатты болып табылады және фазаның магниттік осі мен ротордың бойлы осі арасындағы бұрыштың (2. суреттегі бұрыштары) периодтық функциялары болып табылады.

функцияларының қайталану периоды тең болатын шаманы құрайтынын көрсету қиын емес, сонымен қатар берілген функциялар бұрышының жұп функциялары болып табылады. функцияларын Фурье қатарына үлестіре отырып және үлестірудің алғашқы екі мүшесімен шектеле отырып келесі өрнекті қабылдааймыз:

мұндағы

коэффициенттері статордың фазалы орамаларының симметриялығы әсерінен бірдей болады.

Статордың фазалы орамаларының өзіндік индукция коэффициенттері (электрлі тізбектердің өзаралылығы әсерінен ), периодты бұрышының периодтық функциялары болып табылады. Өзара индукция ағындарының магниттік остері, статордың фазалы орамаларының магниттік осьтерінің жылжу бұрыштарының биссектрисаларымен сәйкес келеді, яғни осының салдарынан және функцияларын Фурье қатарына үлестіру келесі түрді қабылдайды:

(1.22)

9- сурет. Синхронды машинаның сұлбалы түрі

коэффициентінің шамасы әрқашанда теріс болатынын атап өтейік, өйткені статордың фазалы орамаларының магниттік осьтері жоғары бұрышқа жылжыған. және коэффициенттерінің шамалары бір біріне шамамен тең болады және келешекте теңдігі қабылданады.

Бойлы және көлденең демпферлі контурлардың қоздыру орамаларының өзіндік индукция коэффициенттері, статор жонбасы цилиндрлі пішінді болуының нәтижесінде тұрақты шамалар болып табылады.

Статордың фазалы орамалар контурының және қоздыру орамасы контурының өзара индукция коэффициенттері , периодты бұрышының периодтық функциялары болып табылады, өйткені қоздыру орамасының ағыны, ротордың осіне тура бейімделген. функцияларын Фурье қатарына үлестіру келесі түрді қабылдайды:

мұндағы статордың фазалы орамаларының магниттік осьтерінің және қоздыру орамасы бағыттарының сәйкес келуі кезінде орын алатын, өзара индукция коэффициентінің амплитудалық мәні.

Машинаның осінде қоздыру орамасы мен бойлы демпферлі контур орамасының жалпы өзара ағынының бар болуы жөнінде ықтималдықты енгізейік.

Берілген ықтималдықты қабылдау теңдіктеріне келтіреді. Дәл осылайша, фазалы орамалар контурларының және көлденең демпферлі контурдың өзара индукция коэффициенттері үшін келесі қатынастар орын алады:

.

.

Қоздыру орамасы крнтурының және бойлы демпферлі контурдың өзара индукция коэффициенті тұрақты шама болып табылады , өйткені берілген контурлар бір біріне қатысты қозғалмайтын болып табылады және оның магниттік осьтері бағыттас болады.

Синхронды машина роторының айналуы кезінде, жалпы жағдайда еркін бұрыштық жылдамдықты бұрышы сәтінде келесі шаманы құрайды:

, (1.23)

Синхронды тең болатын тұрақты айналым жылдамдығы кезінде, бұрышының уақыт ішінде өзгеруі теңдігімен анықталады, яғни болған кезде де бұрышына тәуелді, синхронды машина орамаларының индуктивтіліктері периодтық функциялар болады.

Синхронды машинаның шартындағы кернеулер балансының дифференциалды теңдеулері келесі түрде болады:

, (1.24)

Аталған теңдеулер периодты өзгеретін өзіндік индукция және өзара индукция коэффициенттерінен ( индуктивтіліктер матрицасы) құралады, бұл олардың аналитикалық түрде шешуін алуғы қиындықтар тудырады. Жаңа үлгідегі қуатты есептеуіш техника құралдарының болмауы салдарынан, аталған жағдай, синхронды машиналардан құралатын үшфазалы тізбектердегі өтпелі үрдістерді есептеу нәтижелерін алуда жоғары техникалық қиындықтар тудырған.

Қозғалмайтын А,В,С координаталар жүйесінде жазылған алғашқы теңдеулерді сызықты түрлендіру, түрдегі фазалы айнымалыларды айнымалыларына алмастырудан құралады. Аталып өткен, айнымалыларды алмастыру үрдісі, алғашқы қозғалмайтын А,В,С координаталар жүйесінің, синхронды машина роторының және симметрия осьтерімен тығыз байланысты және жиілікпен ротормен бірге айналатын, ортогоналды координаталар жүйесіне ауысу жолымен жүзеге асырылады. Сызықты түрлендіру нәтижесінде, құрамында периодтық өзгермейтін коэффициенттер болмайтын, қысқарған түрдегі теңдеулерді аламыз.

Статорлы теңдеулер үшін сызықты түрлендірулер, келесі түрдегі матрица көмегімен жүзеге асырылады:

(1.25)

Бұл теңдеу алғашқы рет Парк ғалымымен /2/ енгізілген.

Мысалға, түрлендірілмеген алғашқы шамалар фазалы тоқтары болсын, ал түллендірілген - тоқтары болсын. Сонда құрастырушы тоқтар үшін сызықты түрлендірулер келесі түрде болады:

, (1.26)

немесе ашық түрде

(1.27)

Статорлы теңдеулер үшін қайта ауысу матрицасы келесі түрді қабылдайды:

(1.28)

Роторлы контурлардың теңдеулері үшін түрлендіру матрицасы 3х3 мөлшерлі бірыңғай Е матрицасын көрсетеді.

Сызықты түрлендірудің толық матрицасы торлы матрица болып табылады, өз кезегінде торлардың әрқайсысы 3х3 мөлшерлі матрица болып табылады.

, (1.29)

яғни статорлы және роторлы түрлендіру матрицаларының тура соммасы болып табылады.

Синхронды машинаның алғашқы үшфазалы қысқа тұйықталу моменті. Аса өтпелі э.қ.к. және машиналар реактивтіліктері.

Бос жүріс режимінде жұмыс істейтін, яғни алғашқы шартындағы, синхронды машинаның статорлы тізбегіндегі, үшфазалы қысқа тұйықталудың пайда болуының алғашқы моментін қарстырайық.

Зерттелетін талапты қысқарту үшін, келесі ықтималдықтарды енгіземіз:

ротордың бұрыштық жылдамдығы тұрақты, яғни сырғуы ;

статорлы орамаларда индуцияланатын трансформаторлы э.қ.к. и есепке алмайық

статор фазаларының және ротор контурларының активті кедергілірін нолге тең деп қабылдаймыз.

Аталған ықтималдықтарды есепке ала отырып, синхронды машинаның теңдеулерін келесі түрде көрсетеміз:

.

Роторлы контурлар теңдеулерінің түрі, бойлы және көлденең демпферлі контурларының қоздыру орамасының ағын берілістері, қабылданған ықтималдықтарда, қысқа тұйықталу сәтінде үздіксіз ғана бола қоймайды, сонымен қатар кейінгі уақытта да тұрақты мәнін сақтайтыны жөнінде қорытындыға келтіреді.

Шынайы машинада берілген жағдай тек алғашқы момент үшін дұрыс болады, ал келешекте аталған ағын берілістері экспоненциалды заң бойынша сөнеді.

Ағын берілістерінің үздіксіздік принципінен шығатын, теңдеулерді машинаның d және q остері бойынша топтап, синхронды машинаның ағын берілістерінің теңдеулер жүйесін зерттейік:

.

Матрицалы түрде берілген жүйе келесі түрді қабылдайды:

Жазбаның таңдап алынған түрінде, матрицасы екі матрицаның тура соммасы болып табылатынын көрсеткен жөн:

мұндағы

.

Ағын берілістердің матрицалы теңдеуінің шешуін келесі түрде іздестіреміз:

мұндағы матрицасына қатысты кері матрица.

Сызықты алгебрадан, матрицалардың тура соммасының кері матрицасы, кері матрицалар-қосындылардың тура суммасына тең болатыны белгілі.

(1.30)

кері матрицасының жоғарыда алынған жазба түрі, машинаның d және q остерінде бөлек орналасқан орамалар үшін шешулер талдауын орындауға мүмкіндік береді.

Машина статорының фазалы кернеулері, үшфазалы қысқа тұйықталу сәтінде келесі өрнекпен сипатталсын дейік

,

мұндағы уақыт сәтінде бірге тең болатын мәннен, секірме түрде нольдік мәнге дейін өзінің мәнін өзгертіп отыратын, жеке сатылы функция (дельта-функция); фазалы кернеудің әрекеттік мәні.

d, q, o координаталар жүйесінде берілген өрнек келесі түрді қабылдайды:

.

Бұл кездегі өтпелі үрдіс синхронды машинаның тек бойлы d осінде ғана орын алатыны анық.

Қарастырылып отырған уақыт сәтіндегі бойлы q осі бойынша сипаттайтын синхронды машинаның реактивтіліктерін анықтау үшін кері матрицасын тауып алайық:

, (1.31)

Кері матрицасындағы элементтердің жазбасында, синхронды машина орамалары индуктивтіліктерінің келесі қосындыларға үлестірілуі қолданылады: статор орамасы сейілуінің ағын берілістері , қоздыру орамалары , демпферлі контурлар , машинаның бойлы және көлденең осьтері бойынша өзара индукция ағын берілістері, яғни

Сонымен қатар келесі белгіленулер енгізілген:

синхронды машинаның бойлы осі бойынша аса өтпелі реактивтілік

(1.32)

Машинаның бойлы осі бойынша активті реактивтілігі

.

матрицасының бас диагоналі бойынша орналасқан меншікті өткізгіштер машинаның сәйкесті орамаларының қыспаларына қатысты кірістік өткізгіштерді сипаттайды. Синхронды машина статорының бойлы орамасы қыспаларына қатысты, кірістік өткізгіштікпен және оған жауап беретін аса өтпелі реактивтілікпен сипатталады.

немесе

өрнегі бойынша анықталатын алдыңғы қысқа тұйықталу режиміндегі синхронды машинаның статорындағы кернеудегі есептеуді орындай отырып, кері матрицасын аламыз:

, (1.33)

Қарастырылғанның аналогиясы бойынша:

синхронды машинаның көлденең осі бойынша аса өтпелі реактивтілік

,

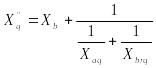көлденең ось бойынша эквивалентті реактивтілік

.

Сонымен, статордағы үшфазалы қысқа тұйықталудың пайда болуының алғашқы сәтіндегі синхронды машина бойлы ось бойынша аса өтпелі және көлденең ось бойынша кедергілерімен сипатталады.

Ағын берілістердің үздіксіздігіне байланысты, үшфазалы қысқа тұйықталудың пайда болуының алғашқы сәті үшін, машинаның бойлы және көлденең осьтері бойынша аса өтпелі э.қ.к. әрекеттік мәндерін келесі өрнектермен анықтаймыз:

,

мұндағы алдыңғы жүктемелі режимдегі синхронды машинаның кернеу мен тоқ құрастырушылары.