2 Расчет параметров циклического кода

• Количество информационных символов

k=16 двоичных символов.

• Длина кодовой последовательности

n=31 двоичных символов.

• Минимальное кодовое расстояние

d₀=7.

• Вероятность ошибок в канале связи

P_k=10^-3.

• Абсолютная избыточность

l=n-k=31-16=15 двоичных символов.

• Относительная избыточность

r=((n-k)/n)*100%=((31-16)/31*)100%=(15/31)*100%≈48.3%.

• Скорость передачи кода

R=k/n=16/31≈0.52.

• Общее количество кодовых последовательностей

К_общ=2ⁿ=2³¹=2147483648.

• Количество разрешенных кодовых последовательностей

К_разр=2^k=2¹⁶=65536.

• Количество проверочных кодовых последовательностей

К_пров=2^n-k=2^31-16=32768.

• Количество исправляемых ошибок

t_испр ≤ (d₀-1)/2=(7-1)/2=3.

• Количество исправляемых ошибок

t_обн ≤ d₀-1=7-1=6.

• Вероятность ошибочного декодирования

• Порождающая матрица G_16,31(x):

• Проверочная матрица H_15,31(x):

• Система раздельных проверок (СРП):

a₁ = a’₁

2 3 6 19 20

5 11 13 24 25

7 14 15 28 29

8 9 21 23 26

4 10 17 30 31

12 16 18 22 27

3 Разработка структурной схемы кодека

3.1 Разработка структурной схемы кодера

Для разработки структурной схемы кодера определим его основные функции и блоки (узлы).

Основные функции кодера:

• распределение символов входной информации на k (k=16) информационных подпотоков;

• формирование l=n-k (l=15) проверочных символов;

• формирование "n" (n=31) кодовых символов путем объединения "k" (k=16) информационных и "l" (l=15) проверочных символов в единый кодовый поток.

Основные узлы кодера:

• К – коммутатор;

• ФПСк – формирователь проверочных символов кодера;

• ФСУк – формирователь сигналов управления ключами кодера;

• Кл – ключи управления.

Кодер, состоящий из перечисленных блоков, будет реализовывать следующий алгоритм формирования циклического кода:

1. G(x)x^(n-k), то есть информационный полином G(x) умножается на x в степени равной степени порождающего многочлена r = (n - k). Умножение полинома на x^r означает сдвиг на r разрядов влево.

2. , то есть произведение G(x)x^(n-k) делится на порождающий многочлен P(x) и определяется частное Q(x) и остаток от деления R(x). Степень R(x) всегда ниже степени порождающего многочлена.

3. F(x) = G(x)x^(n-k) R(x), то есть комбинация циклического кода строится как совокупность информационных элементов и приписанных к ним со стороны младших разрядов элементов остатка (проверочных элементов).

Обобщенная структурная схема кодера будет иметь построение, показанное на рисунке 1.

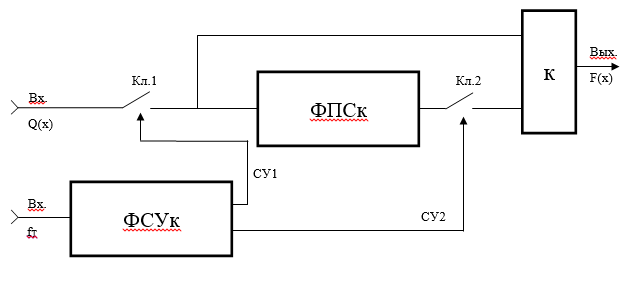
Рисунок 1 – Структурная схема кодера

Кроме того, кодовая последовательность F(x) может быть создана по правилу F(x)=Q(x)⋅G(x): первый символ Q(x) умножаем на первый символ первого столбца G(x), второй символ Q(x) умножаем на второй символ первого столбца G(x) и суммируем по модулю два с первым результатом, третий символ Q(x) умножаем на третий символ первого столбца G(x) и суммируем по модулю два с предыдущим результатом и т. д. Затем первый символ Q(x) умножаем на первый символ второго столбца G(x) и далее все повторяется аналогично формированию первого кодового символа F(x). При данном способе кодирования для получения разделимого кода необходимо, чтобы порождающая матрица имела канонический вид.

В данном курсовом проекте используется метод создания кодовой последовательности по правилу F(x)=Q(x)⋅G(x).