1.7 Мажоритарный алгоритм декодирования циклических кодов

Название алгоритма мажоритарного декодирования вытекает из самой сущности реализации алгоритма декодирования, а точнее от способа принятия решения о полярности (знаке) декодируемого информационного символа. При мажоритарном алгоритме декодирования решение о полярности декодируемого информационного символа принимается по большинству одинаковых результатов решения проверочных уравнений (проверок); реализуется принцип “голосования”. Это означает, что если более 50% результатов решения проверочных уравнений имеют значения логической “1” или логического “0”, то декодер формирует соответственно информационные символы равные “1” или “0”. При равном количестве результатов решения проверочных уравнений условно принято, что декодер формирует нулевой информационный символ, т.е. решение принимается в пользу”0”.

Систематические линейные коды обладают следующим свойством: если принятую кодовую последовательность F'(x) умножить на транспонированную проверочную матрицу кода H^т_l,n(x), то можно получить следующие два результата:

F'(x)·H^т_l,n(x)=0 и F'(x)·H^т_l,n(x)≠0.

Результат решения первого уравнения означает, что в принятой кодовой последовательности ошибок нет или ошибки не обнаруживаются кодом. Результат решения второго уравнения противоположен первому.

Так как любой ЦК имеет l проверочных символов, то можно составить 2^l проверочных уравнений вида F'(x)·H^т_l,n(x)=0. В общем виде проверочное уравнение для некоторой j-ой строки транспонированной проверочной матрицы H^т_l,n(x) можно записать так [9]:

Используя же свойство цикличности кода, то можно построить и все 2^l проверочных уравнений, что можно записать так [1,2,3,6]:

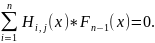
Главной задачей алгоритма мажоритарного декодирования является выбор или составление “хорошего” или “оптимального” (в плане обеспечения максимальной корректирующей способности кода) подмножества проверочных уравнений; при условии, если оно существует.

Наиболее “просто” составляются проверочные уравнения, в основе которых лежит следующая идея: если декодируемый информационный символ входит во все проверочные уравнения, а остальные символы, входящие в эти проверочные уравнения, входят только по одному разу. Данную идею можно записать в виде следующей системы проверочных уравнений относительно некоторого информационного символа, например, а_j:

а_j=k⊕m⊕γ⊕…⊕ξ,

а_j=F⊕N⊕G⊕…⊕C.

Записанная система проверочных уравнений носит название “системы раздельных проверочных уравнений (проверок)” – СРП. Исходя из вышеизложенного следует: если множество µ (µ ≥ 2) проверочных уравнений (n,k)-кода ортогональны относительно некоторого символа и данный символ входит во все проверочные уравнения, а все остальные символы, входящие в эти проверочные уравнения, входят только в одно проверочное уравнение, то к данному (n,k)-коду возможно применение алгоритма мажоритарного декодирования и при этом будет гарантировано обеспечиваться коррекция ошибок кратностью t_исп≤ µ /2 двоичных символов.

Таким образом, при требуемой или заданной корректирующей способности кода синтез кодека, реализующий алгоритм мажоритарного декодирования, включает выполнение следующих операций (процедур) [9]:

1. определение минимально необходимого количества ортогональных проверочных уравнений, используя равенство µ=2* t_исп+1; последний член данного равенства характеризует, так называемое, тривиальное уравнение относительно декодируемого информационного символа, например, a_i=a'_i;

2. построение проверочной матрицы H(x) либо в канонической форме, либо в транспонированной форме;

3. формирование по построенной проверочной матрице системы раздельных проверок;

4. разработка структурных, функциональных и принципиальных электрических схем кодека;

5. проверка коррекции кодеком ошибок заданной кратности.