2.2 Разработка модели тепловых процессов в коммерческом пакете ansys

Процессы теплопередачи происходят в пространстве и времени. Поэтому исследование теплопроводности сводится к изучению пространственно-временного изменения температуры, т. е. к нахождению зависимости 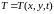, где – пространственные координаты в декартовой системе, t – время.

Совокупность значений температуры во всех точках изучаемого пространства называется температурным полем. Различают стационарные и нестационарные температурные поля. Нестационарным температурным полем называется такое поле, температура которого изменяется не только в пространстве, но и с течением времени. Стационарным температурным полем называется такое поле, температура которого в любой его точке не изменяется во времени [9].

Для решения задач, связанных с нахождением температурного поля, необходимо иметь дифференциальное уравнение теплопроводности, которое дает зависимость между температурой, временем и координатами элементарного объема. В декартовой системе координат уравнение теплопроводности для изотропных материалов имеет вид:

где λ - коэффициент теплопроводности, c – теплоемкость, ρ – плотность, ω – мощность тепловыделения.

Дифференциальное уравнение теплопроводности описывает перенос тепла внутри тела. Для того чтобы найти температурное поле внутри тела в любой момент времени, т. е. решить дифференциальное уравнение, надо знать геометрическую форму тела и краевые условия. Краевые условия состоят из начальных и граничных условия.

Начальные условие представляют собой распределение температуры в начальный момент времени, т. е.

(X, Y,0) ,

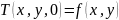
где f - известная функция.

Во многих нестационарных задачах принимают равномерное распределение температуры в начальный момент времени:

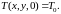
Граничные условия определяют закон взаимодействия между окружающей средой и поверхностью тела. Граничные условия могут быть заданы различными способами:

Граничное условие первого рода задает распределение температуры по поверхности тела в любой момент времени, т. е.

где - температура поверхности тела.

В частном случае, то есть температура на поверхности постоянна на протяжении всего процесса теплообмена. Это может быть осуществлено при искусственном поддержании постоянной температуры или при особых условиях теплообмена (см. граничное условие третьего рода).

Граничное условие второго рода состоит в задании плотности теплового потока для каждой точки поверхности тела как функции времени, т. е.

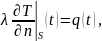
где - нормаль к граничной поверхности S.

Простейший случай граничного условия второго рода состоит в постоянстве плотности теплового потока:

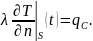
Такой случай теплообмена имеет место при нагревании тел в высокотемпературных печах, где передача тепла в основном происходит при помощи излучения по закону Стефана-Больцмана, когда температура тела значительно меньше температуры излучающих поверхностей.

3. Граничное условие третьего рода характеризует закон конвективного теплообмена между поверхностью тела и окружающей средой (закон Ньютона). В этом случае количество тепла, передаваемого в единицу времени с единицы площади поверхности тела в окружающую среду с температурой , прямо пропорционально разности температур между поверхностью тела и окружающей средой, т. е.

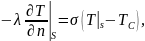
где σ - коэффициент теплообмена.

4. Граничное условие четвертого рода соответствует теплообмену поверхности тела с окружающей средой или теплообмену соприкасающихся твердых тел. При этом имеют место соотношения:

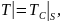
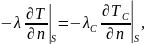
т. е. на границе соприкосновения обеспечивается равенство температур и равенство потоков тепла [8].

Чтобы функция 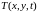была решением тепловой задачи необходимо, чтобы она удовлетворяла дифференциальному уравнению, начальным и граничным условиям. В случае стационарной задачи начальные условия отсутствует.

По теореме единственности решения, если некоторая функция T удовлетворяет выше указанным условиям, то она является единственным решением данной задачи.

В инженерных тепловых задачах имеют место конечные объемы сложной геометрической формы, произвольные граничные условия и материалы с нелинейными характеристиками. Поэтому для решения тепловых задач в инженерной практике применяются численные методы [9].

В рамках дипломной работы была создана математическая модель электромагнитных и тепловых процессов при индукционном нагреве ленты в двухмерной постановке на базе коммерческого пакета ANSYS. Структура разработанной модели показана на Рисунке 7.