1. 4 Выводы по главе

1. Выделены основные особенности и показана необходимость использования проходного индукционного нагрева трубопроводов.

2. Представлены методы термической обработки стальных труб.

3. Проведен анализ свойств индукционной системы нагрева.

4. Представлены параметры математического описания нагрева трубы в продольном магнитном поле.

2 Математическая модель индукционных систем

Для получения необходимой точности при моделировании индукционного нагрева, программное обеспечение должно учитывать следующие факторы:

1. Тепловые и электромагнитные явления сильно связаны. Это вызвано зависимостью свойств металлов (удельное сопротивление, теплопроводность, теплоемкость) от температуры. Кроме этого, относительная магнитная проницаемость зависит от температуры и напряженности магнитного поля.

2. При проектировании оборудования для индукционного нагрева необходимо принимать во внимание нестационарные процессы, которые могут быть вызваны загрузкой, разгрузкой, процессом термостатирования и т.п.

3. В современных непрерывных технологиях, таких как непрерывная разливка - непрерывная прокатка, горячая гальванизация и т.п., индукционная печь работает совместно с другим оборудованием (например, с газовыми печами), которое оказывает сильное влияние на её работу (начальное температурное поле в заготовке).

Игнорирование этих факторов может привести к серьёзным ошибкам при проектировании установок индукционного нагрева.

В общем случае математическое описание таких объектов представляет собой систему детерминированных нелинейных дифференциальных и интегральных уравнений, записанных для многомерных и многосвязных областей. Методы математической физики, в том числе метод разделения переменных Фурье, метод источников, операционные методы, методы интегральных преобразований, позволяют эффективно решать узкий круг задач с большим количеством допущений. Если не вводить существенных упрощений в постановку задачи, то

решение указанной системы уравнений, а значит, и количественное описание изучаемых объектов может быть получено только с использованием численных методов через моделирование на ЭВМ [7].

2. 1 Разработка модели электромагнитных процессов в коммерческом пакете ansys

Для решения электромагнитных и тепловых задач, а также определения физических сил и механических усилий существует большое количество различных коммерческих программ. В настоящее время наиболее распространенным универсальным инструментом является программный пакет ANSYS, предназначенный для проведения анализа и численного решения широкого круга инженерных задач (механика, теплофизика, гидрогазодинамика и электромагнетизм) и базирующийся на методе конечных элементов.

Электромагнитное поле в среде ANSYS описывается уравнениями Максвелла. Уравнение непрерывности выводится, используя оператор div :

Уравнение непрерывности должно быть удовлетворено надлежащей системой уравнений Максвелла. Вышеприведенные уравнения должны быть дополнены материальными уравнениями, описывающими закономерности электромагнитных материалов. Уравнение связи магнитной индукции и напряженности магнитного поля для задач, учитывающих насыщающийся материал без постоянных магнитов:

,

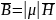где – матрица магнитных проницаемостей, может быть задана как функция температуры и/или напряженности поля. Если – функция температуры:

,

где – магнитная проницаемость вакуума, – магнитная проницаемость в направлении x.

Если – функция магнитного поля (только для двухмерной задачи):

,

где – проницаемость, зависящая от напряженности магнитного поля.

Если – функция напряженности магнитного поля и температуры:

,

Дифференциальная формулировка закона электромагнитной индукции для движущихся тел и уравнение связи индукции и напряженности электрического поля:

,

,

где – матрица диэлектрических проницаемостей, – диэлектрическая проницаемость в направлении оси x,

,

,

где – вектор скоростей.

Для решения задач, связанных с магнитным полем, как правило, используется векторный и скалярный потенциалы (магнитный векторный потенциал и скалярный электрический потенциал). В зависимости от задачи используется тот или иной потенциал. Факторы, влияющие на выбор это: динамика поля, размерность, дискретизация и размер области (домена).

В численной модели используется элемент, в котором применен метод магнитного векторного потенциала, учитывается статическое и динамическое поле, пренебрегается токами смещения, используется следующее подмножество уравнений Максвелла [8].

Решение может быть получено введением магнитного векторного потенциала A такого, что:

,

и электрического скалярного потенциала V такого, что:

,

Результирующие дифференциальные уравнения для токопроводящей и магнитно-проницаемой области:

,

,

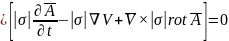и для не токопроводящей области:

.

Базовое решение задачи электромагнитного поля включает напряженность магнитного поля, плотность магнитной индукции, электромагнитные силы и плотности тока.

Напряженность магнитного поля находится первой при помощи операции вычисления ротора магнитного векторного потенциала.

,

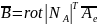где – функция формы элемента, 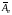– узловой векторный магнитный потенциал.

Далее напряженность магнитного поля находится из магнитной индукции:

,

где – матрица удельного магнитного сопротивления.

Для переходного анализа также находятся плотности тока:

,

где – полная плотность тока,

где – плотность тока, обусловленная 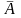, 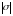– матрица проводимостей, n – число

точек интегрирования, – производная по времени от магнитного векторного потенциала:

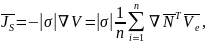
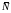где – электрический скалярный потенциал, – функция формы элемента для V, вычисленной в точках интегрирования:

,

где – вектор приложенной скорости.