1. 3. 3 Труба во внешнем магнитном поле. Математическое описание

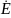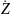Распределения , и ₀ по стенке цилиндра описываются выражениями с принятыми 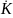_в = т_в /2. В предельном слу­чае низкой частоты (f = f₁) постоянна по сечению, а меняется линейно (Рисунок 6.1). При высокой частоте (f = f₄) распределения близки к экспоненциальным.

Для принятой нами формы записи коэффициенты G и Q приведены на рисунке 6.2 в функции относительной толщины стенки ∆m. Дадим фи­зическое толкование кривым G = f (∆m). Возьмем случай сравни­тельно большого внутреннего ради­уса (т_в 5), когда максимум G яс­но выражен. При малой толщине (∆m 0,1) собственное активное со­противление стенки велико и инду­цированные в ней токи мало вли­яют на напряженность 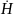_в и, следовательно, на магнитный по­ток _в в полости. Поэтому в каждом слое стенки наводит­ся почти одинаковая ЭДС и с увеличением ее толщины мощ­ность, а следовательно, и G возрастают линейно. Затем начинает сказываться размагничивающее влияние наведенных токов, Н_в и Ф_в уменьшаются, что ведет к замедлению роста G, а начиная с некото­рого значения ∆m, и к его падению. Одновременно увеличивается роль потока в стенке, полость перестает заметно влиять на электри­ческие параметры и G стремится к единице. Небольшой минимум G, обычно наблюдаемый при d πδ/2 (∆m 2,2), объясняется фа­зовыми соотношениями, как и при одностороннем проникновении волны в пластину. Хорошие результаты дают полуэмпирические формулы [2]

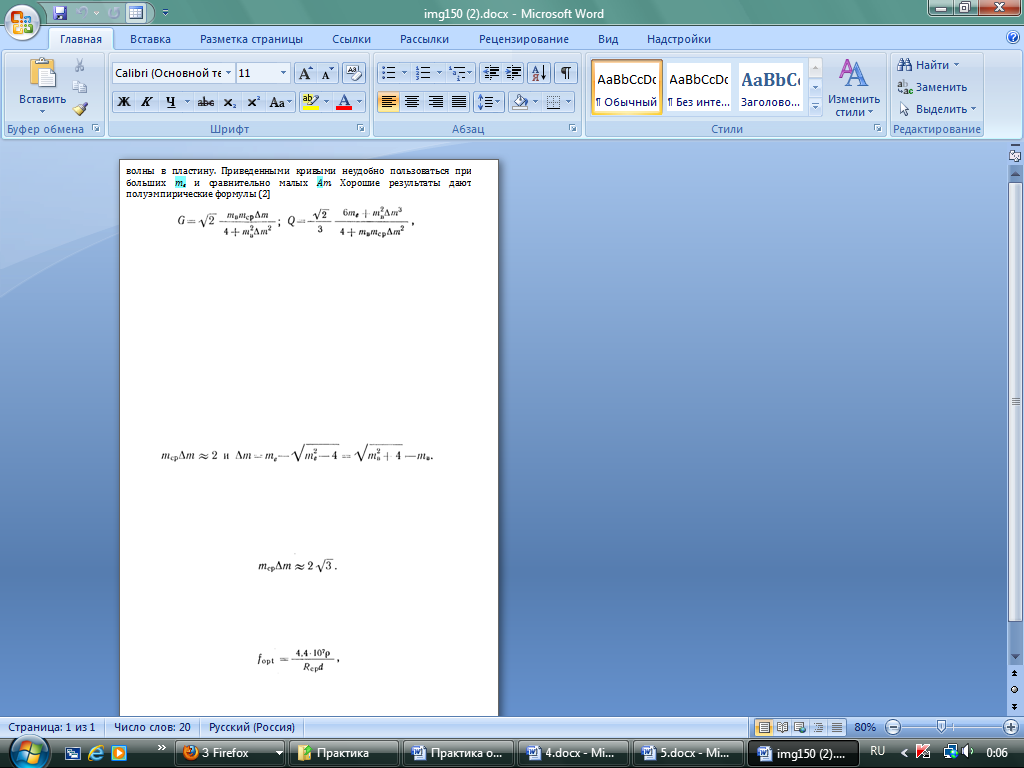
(1.1)

где m_ср = 0,5 (m_в + т_е).

Чем меньше толщина стенки и больше радиус, тем точ­ность выше.

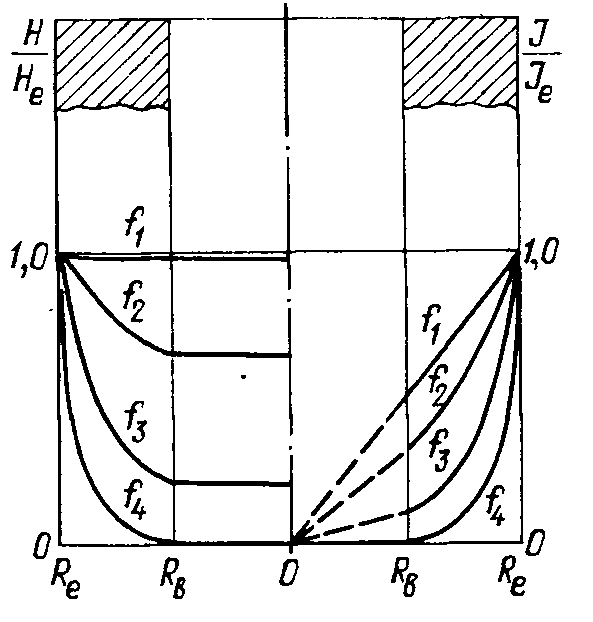
Рисунок 6.1 - Распределение напряженности магнитного поля и плотности тока по тол­щине стенки полого цилиндра без магни­топровода

Рисунок 6.2 - Зависимости коэффициентов активного (G) и реактивного (Q) сопротивлений полого цилиндра от его радиуса и толщины стенки

1. 3. 4 Оптимальные частота и толщина стенки

Так как приближенные формулы обеспечивают достаточную точность в области максимума G, их удобно использовать для определения оптимальных условий нагрева. В качестве критерия оптимальности принимаем максимум электрического КПД.

Пусть частота постоянна, а толщина стенки меняется. Такая ситуация характерна для конструирования индукционных систем для обогрева оборудования, а также для выбора номенклатуры из­делий, которые целесообразно нагревать при заданной частоте. Считая, что с изменением толщины стенки отношение радиуса трубы т_е к радиусу индуктора сохраняется, получаем условие максимума КПД dG/d (∆m) = 0, откуда

Из этих выражений следует, что при т_е 2 максимум G от­сутствует, что подтверждается расчетом по точным формулам. Опти­мальная толщина стенки соответствует условию R_cpd δ². Макси­мальное значение G при этом примерно равно m_ср/4.

Пусть теперь размеры трубы постоянны, а частота выбирается из условия максимума КПД. Беря производную G по частоте, по­лучаем

(1.2)

Таким образом значение т_ср∆т, соответствующее максимуму КПД при изменении частоты, в 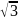раз больше, чем при изменении толщины стенки.

Из (1.2) оптимальная частота для нагрева длинных полых цилиндров

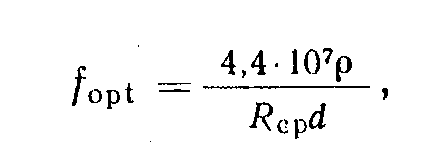
(1.3)

где R и d— в см, ρ — в О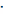м см.

При сокращении длины индукционной системы частота соответствующая максимуму КПД, возрастает [2, 10].