4.5.Качество оценки: коэффициент детерминации r2

Цель регрессионного анализа состоит в объяснении поведения зависимой переменной y. В любой выборке y оказывается уравнительно низким в одних наблюдениях и сравнительно высоким ‑ в других. Мы хотим знать, почему это так.

Разброс значений y в выборке можно описать с помощью дисперсии. Обозначим выборочную дисперсию через Var(y).

В парном регрессионном анализе мы объясняем поведение y его зависимость от х. Построив регрессионную зависимость, можно разбить значение y на две составляющие:

,

(0)

где - расчетное (прогнозируемое) значение в точке i,

e_i ‑ остаток между фактическим и cпрогнозированным значением, то есть та часть у_i, мы уже не можем объяснить уравнением регрессии.

Можно доказать, что

,

(0)

Таким образом, мы можем разложить дисперсию у на две части:

‑ часть дисперсии, «объясненная» уравнением регрессии,

‑ «необъясненная» уравнением регрессии часть.

Следовательно, ‑ это доля дисперсии у, объясненная уравнением регрессии. Это отношение известно как коэффициент детерминации R²:

,

(0)

Таким образом, коэффициент детерминации, характеризует долю дисперсии у, объясненной регрессией y по x.

Из (0) получаем:

,

(0)

что равносильно:

.

(0)

Максимальное значение коэффициента детерминации равно 1: R²=1. Это происходит в том случае, когда линия регрессии точно соответствует всем наблюдениям, то есть линия регрессии проходит точно через все y_i, и все остатки равны нулю: e_i=0.

Если видимая связь между y и x отсутствует, то R² близок к 0.

Желательно, чтобы R² был больше. То есть мы выбираем a и b так, чтобы максимизировать R².

Это не противоречит тому, что надо минимизировать сумму квадратов отклонений , выраженную уравнением (0).

Действительно,

.

(0)

Следовательно, из выражений (0) и (0) получим:

.

(0)

Итак, на основании выражения (0) можно сделать вывод о том, что принцип минимизации суммы квадратов остатков эквивалентен максимизации коэффициента детерминации R².

Альтернативное представление для коэффициента детерминации – представление через суммы квадратов отклонений.

Рассмотрим возможные отклонения y, связанные с моделью регрессии. Справедливо соотношение:

.

(0)

Здесь

‑ общее отклонение;

‑ остаток;

‑ отклонение, объясненное регрессией.

Заметим, что

.

(0)

Тогда из (0) получаем:

.

(0)

Следовательно, общая сумма квадратов отклонений равна сумме квадратов отклонений, объясненных регрессией плюс сумма квадратов остатков:

.

(0)

Здесь

‑ общая сумма квадратов отклонений;

‑ сумма квадратов отклонений, объясненных регрессией;

‑ сумма квадатов остатков.

Выражение для коэффициента детерминации через суммы квадратов отклонений будет иметь вид:

.

(0)

На интуитивном уровне представляется очевидным, что чем больше соответствие, обеспечиваемое уравнением регрессии, то есть между фактическим и прогнозным значениями объясняемой переменной y, тем больше должен быть коэффициент корреляции между y и .

Можно доказать, что коэффициент детерминации равен квадрату коэффициента корреляции между фактическим и прогнозным значениями y:

.

(0)

Здесь ‑ выборочная ковариация между y и .
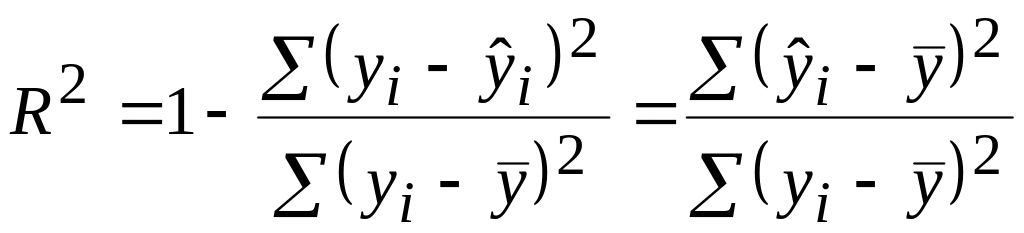
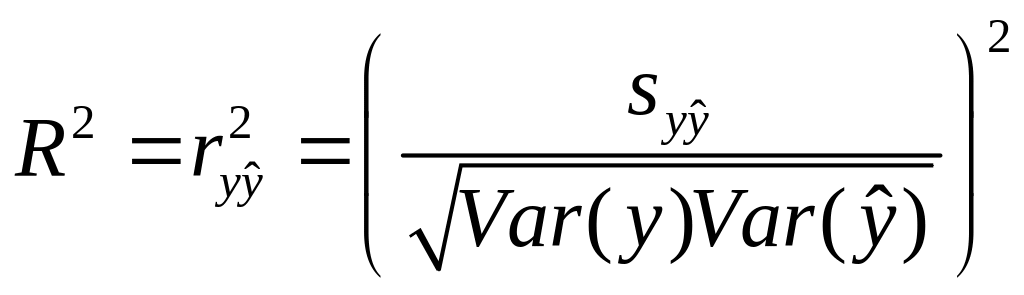