1. Особенности движения автомобилей по кривой

На автомобиль, движущийся по кривой в плане в точке с радиусом R, действует центробежная сила:

, (4.1)

где m – масса автомобиля;

v – скорость движения.

Центробежная сила направлена перпендикулярно к движению автомобиля и оказывает на него опрокидывающее и сдвигающее воздействие. Под влиянием этой силы деформируются шины в поперечном направлении, что приводит к повышенному износу шин и увеличению расхода топлива. В ночное время свет фар освещает на криволинейном участке меньшую длину дороги, чем на прямолинейном участке. При движении по кривой на автомобиль действуют две силы, приложенные к его центру тяжести:

C – центробежная сила; G – вес автомобиля.

Проектируя эти силы на направление поперечного уклона, получаем поперечную силу:

Рис.4.1. Расчетная схема (4.2)

Но cos α≈1; sin α≈tg α=i ; G=m·g . Тогда:

, (4.3)

Откуда, (4.4)

(4.5)

Тогда, значение радиуса кривой в плане будет определяться по формуле:

(4.6)

где: v – расчетная скорость автомобилей;

g – ускорение свободного падения;

μ - коэффициент поперечной силы;

i - поперечный уклон проезжей части.

Коэффициент поперечной силы (μ), учитывает влияние на автомобиль и пассажиров центробежной силы:

при μ < 0,10 – кривая пассажирами не ощущается;

при μ = 0,20 – кривая ощущается и пассажир испытывает неудобства (рекомендуется принимать для обеспечения удобства движения пассажира по кривой);

при μ = 0,30 – въезд с прямого участка на кривую ощущается как толчок, наклоняющий пассажиров в бок;

при μ > 0,6 – автомобиль может опрокинуться.

2. Переходные кривые

В момент въезда автомобиля с прямого участка на кривую в плане скорость движения автомобиля снижают, т.к. на автомобиль начинает действовать центробежная сила. Чтобы в момент поворота колес не происходил занос автомобиля, между прямым участком и кривой малого радиуса вводят так называемую переходную кривую, в пределах которой кривизна дороги плавно изменяется от 0 (на прямом участке) до 1/R в начале круговой кривой.

На автомобильных дорогах I-III категорий радиусы круговых кривых принимают такими, чтобы автомобили проезжали эти участки без снижения скорости. В этом случае длину переходной кривой рассчитывают из условия движения с постоянной скоростью по формуле:

, (4.7)

где V - расчетная скорость в км/ч;

J - изменение центробежного ускорения, принимаемое 0,4 - 0,6 м/с³;

R - радиус круговой кривой, м.

Переходная кривая, определяемая по формуле (4.7) называется клотоидой (радиоидою).

Угол поворота клотоиды определяется по формуле

(4.8)

и текущие координаты по формулам

, (4.9)

где S – часть длины переходной кривой до данной точки;

С = R·L

При учете движения с переменной скоростью в качестве Рис. 4.2 Расчетная схема переходных кривых проектируют тормозные кривые.

3. Расчет элементов закругления в плане

Последовательность проектирования кривых в плане:

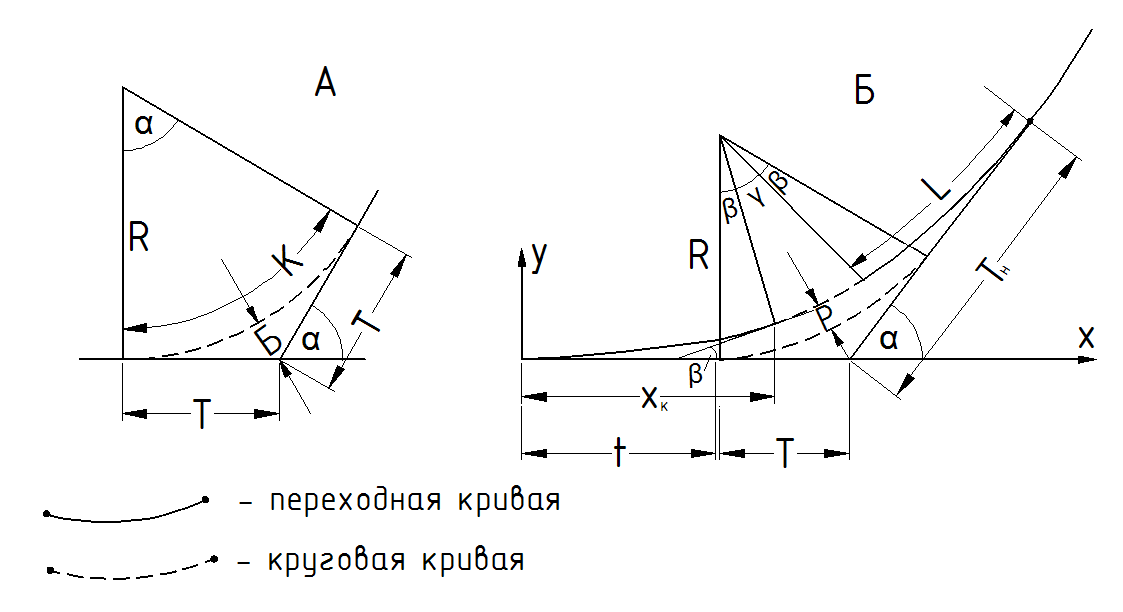
Рис. 4.3 Расчетная схема

1. Определяют элементы закругления:

; (4.10)

; (4.11)

; (4.12)

, (4.13)

где T – тангенс кривой, м;

К – длина кривой, м;

Д – домер, м.

Б – биссектриса, м.

Вычисления производят с точностью до сотых долей метра.

2. На закруглениях с R ≤ 2000м круговые кривые сопрягают с прямыми при помощи переходных кривых (обеспечивающих плавное изменение центробежной силы), в результате чего круговая кривая смещается к центру, а величина тангенса составной кривой увеличивается (рис.4.3). Длина переходных кривых зависит от радиуса закругления и может быть принята с учетом СНиП 2.05.02-85^*.

Таблица 4.1 – Значения переходной кривой

Радиус круговой кривой, м	30	50	60	80	100	150	200	250	300	400	500	600-1000	1000-2000
Наименьшая длина переходной кривой, м	30	35	40	45	50	60	70	80	90	100	110	120	100

3. Вычисляют длину переходной кривой по формуле (4.7):

,

4. Вычисляют угол поворота переходной кривой β между касательной к концу переходной кривой, и осью абсцисс.

(4.14)

и проверяют возможность разбивки переходных кривых, исходя из условия:

. (4.15)

Если это условие не выполняется, необходимо увеличить радиус.

5. Для детальной разбивки определяют конечные координаты переходной кривой по формулам (где С = R·L).

, (4.16)

1. Вычисляют величину смещения (t) тангенса

t = X_К – R·sinβ (4.17)

и величину тангенса составной кривой.

T_Н = T+t. (4.18)

6. Определяют длину оставшейся части круговой кривой

; (4.19)

и длину составной кривой

S = K_О + 2L. (4.20)

6. Вычисляют величину сдвижки кривой (р) внутрь

р = Yк – R(1-cos β) (4.21)

и биссектрису составной кривой

Бн = Б + р. (4.22)

6. Вычисляют домер (Д_Н) составной кривой

Дн = 2Тн – S. (4.23)

6. Значения величин t, β и р приведены в табл. 4.2 в зависимости от длины переходной кривой.

Таблица 4.2 – Значения t, β и р

L, м	40	50	60	70	80	90	100	110	120	100
t, м	19,99	24,95	29,96	34,96	39,97	44,97	49,97	54,98	59,99	50,00
β, º	19º06´	14º19´	11º28´	10º01´	9º10´	8º36´	7º10´	6º18´	3º26´	1º25´58´´
р, м	1,10	1,02	1,00	1,02	1,07	1,12	1,05	1,01	0,60	0,26

4. Виражи

На кривых малых радиусов для повышения устойчивости автомобилей против заноса устраивают односкатный поперечный профиль с уклоном проезжей части и обочин к центру кривой – вираж. Уклон виража зависит от величины радиуса и скользкости дороги.

Участок, на котором поперечный профиль переходит от двускатного к односкатному, называют отгоном виража. Его совмещают с переходной кривой и, если она отсутствует, то устраивают на прямом участке дороги.

Последовательность изменения поперечного профиля:

1 стадия – обочины, как бы вращаются около кромок проезжей части до выравнивания в одну плоскость с уклоном проезжей части (сеч-е 1-1);

2 стадия – наружную половину полотна как бы вращают около оси дороги до выравнивания в одну плоскость с внутренней половиной полотна (сечение 2-2);

3 стадия– все полотно вращают около внутренней

Рис.4.4 Расчетная схема кромки проезжей части до уклона виража (сеч-е 3-3).

Если уклон виража равен уклону проезжей части двускатного профиля (i_в=i_п), то третья стадии отгона виража отсутствует.

Прямая с двускатным профилем

Круговая кривая. Вираж (односкатный профиль)

Переходная кривая и отгон виража

Прямая с двускатным профилем

Переходная кривая и отгон виража

уширение

Рис.4.5 - Общий вид закругления виражом