13. По каким параметрам и как делается заключение об динамической устойчивости сложных ээс.

Процесс интегрирования в принципе бесконечен, поэтому интегрирование нужно вести до тех пор, пока станет возможным заключить эл. система устойчива или нет.

По определению эл. система устойчива,, если после приложения возмущающих и необходимых управляющих воздействий она вновь восстановит исходный или близкий к исходному режим. В случае больших возмущений это означает восстановление синхронной работы генераторов, поэтому наблюдения нужно вести за движением ротора всех генераторов системы.

Обычно следят за взаимными углами ротора δ_ij (t) т.к.

δ_ij = δ_i – δ_j =

Как только скорости роторов генератора устанавливаются равными друг другу, т.е. наступит синхронная работа, взаимные углы роторов генераторов δ_ij перестанут изменяться, таким образом электрическая система будет устойчива, если с течением времени все временные углы ротора генератора будут стремиться к своим новым установившимся значениям.

В действительности достаточно рассматривать не все взаимные углы, а лишь взаимные углы роторов всех генераторов по отношению к ротору одного генератора δ₁₂,δ₁₃,δ₁₄... т.к. прочие углы могут быть выражены δ₂₃= δ₁₃- δ₁₂=( δ₁- δ₃)-( δ₁- δ₂)= δ₂- δ₃

δ ₃₄₌ δ₃- δ_{4 и т.д.}

Нужно иметь в виду, что если при составлении описания переходного процесса для некоторого узла было принято δ₁=const , то взаимные углы всех генераторов по отношению к вектору напряжения этого узла будут совпадать с их собственными углами δ₁

В этом случае заключения об устойчивости системы можно делать по поведению собственных узлов δ_i (t).

14. Оценка устойчивости ээс но методу площадей.

Для простейшей электрической системы при описании переходных процессов в ней уравнениями

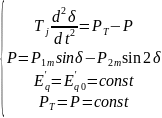
Характер относительного движения ротора эквивалентного генератора станции после отключения К3 можно установить рассматривая энергетические соотношения сил, действующие на ротор.

Определив проводимости схемы У_11, У₁₂ для исходного, аварийного и послеаварийного режима можно построить характеристики мощности генераторов станции для этих режимов

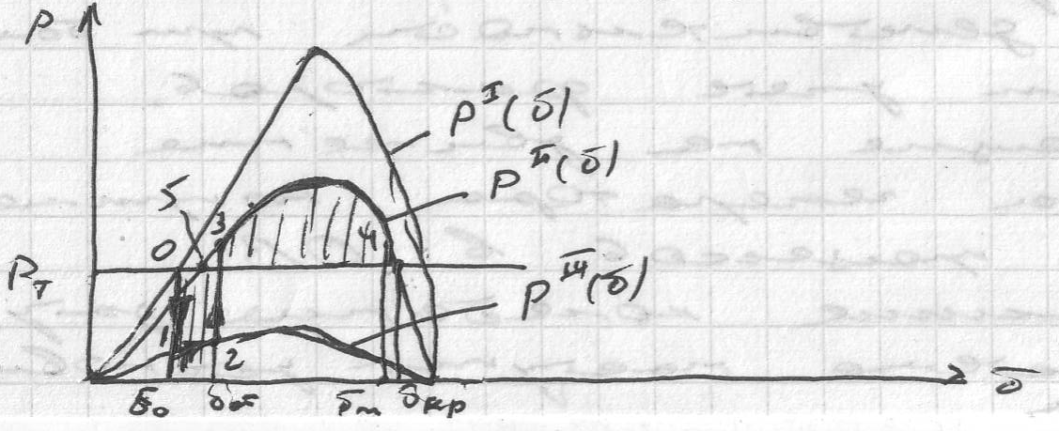
Исходный установившийся режим будет соответствовать (·) 0, когда уравновешены электромагнитные мощность генератора и мощность турбины.

В первый момент δ₍₀₎=δ₀ и поэтому новый режим будет соответствовать (·)1 на хар-ки мощности II режима К3, т.к. теперь генератор будет отдавать меньшую мощность, получаемую от турбины, то над действием избыточного момента ротор начнет ускоряться.

Относительное перемещения ротора отражается уравнениями движения T_J =P_T – P_(δ)

Учитывая, что = · 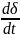= Δω 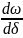, то T_J Δω = P_T – P_(δ)

T_J Δω d Δω = (P_T – P_(δ))dδ

++Интегрируя это уравнение найдем кинетическую энергию , полученную ротором в конце ускорения

A_у = T_J = dδ

Кинетическая энергия, приобретенная ротором в процессе ускорения численно равна заинтегрированной на графике площадки ускорения.

После отключения К3 генератор будет отдавать в сеть мощность большую, чем он получает от турбины. (·)3 на хар-ки после аварийного режима 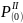Ротор начнет тормозиться теряя приобретенную кинетическую энергию и скорость. Энергия торможения будет равна A_у = T_J = dδ

Она представлена заштрихованной на графике площадкой торможения f_T

В (·)4 относительная скорость ротора Δω=0, т.к. генератор по-прежнему будет отдавать большую мощность, чем он получает от турбин, то в следующий момент его относительная скорость Δω станет меньше 0 и угол δ начнет уменьшаться.

Т.к. принятое математическое описание переходных процессов соответствует позиционной системе, то рассеяние энергии колебаний (избыточной энергии) не будет происходить и поэтому в этом случае энергия ускорения и торможения будут равны А_У=А_Т, равны будут и площадки ускорения и торможения.

Максимально возможная площадка торможения f_T в рассматриваемом случае будет ограничена верхней частью хар-ки мощности послеаварийного режима P^III и хар-ки мощности турбины P_T от δ_0T до δ_ср

Очевидно, что если f_T>f_y, то электрическая система устойчива. Чем больше f_T по сравнению с f_y, тем больше запас динамической устойчивости.