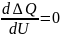4. Определение критических напряжений нагрузочных узлов и больших ээс методом утяжеления режима
Для
определения Uкр
узла нагрузки сложной ЭЭС можно
воспользоваться критерием устойчивости
Определение зависимости Qc, поступающей из сети в узел, при изменении напряжения узла. Можно осуществить методом утяжеления режима по напряжению этого узла.
Вначале должны быть рассчитан, исследуемые на устойчивость режим ЭЭС и ЭДС источников с учетом имеющихся у них систем РВ. Модули и фазовые углы рассчитанных ЭДС в дальнейшем расчете остаются неизменными. Далее определяется Uкр тех узлов, устойчивость нагрузки которых нужно проверить.
Пусть для определения Uкр выбран узел K; система уравнений, описывающая состояние(режим) ЭЭС в рассматриваемых условиях выглядит так
Решая эту систему уравнений при заданной величине модуля напряжения узла K Uk(l) определим напряжение узлов и по ним реактивную мощность, поступающую из сети
Расчет следует повторить для ряда постепенно снижаемых уровней напряжения узла(0,95Uko,0.9Uko….-Uko в исходном режиме)
В результате получить зависимость ∆Q(Uk) и определить Uкр узла
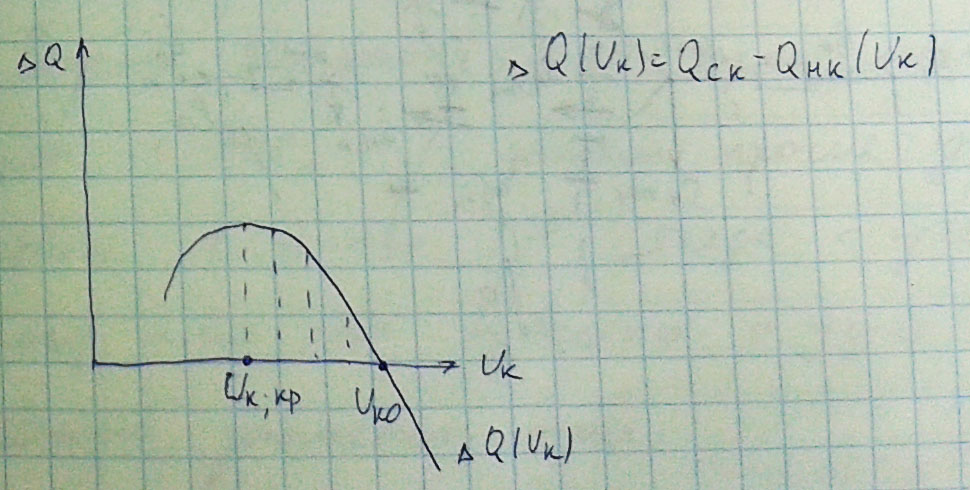
Обследованию подлежат прежде всего узлы с большим потребление, а так же элементы удаленные от источника(большое сопротивление)
5.Определение пределом передаваемой мощности сложных ээс путем преобразования исходной схемы к звездообразной.
Пусть для сложной ЭЭС был рассчитан некоторый планируемый режим. При расчете этого режима были рассчитаны также и ЭДС Ex, приложенные за сопротивление Х (в зависимости от типа АРВ).
Выполнено преобразование исходной схемы замещения к звездообразной.
Пусть в начале были пронумерованные узлы с ЭДС 1…n, а затем прочие узлы n+1…N, тогда считая ЭДС известными системными уравнениями узловых напряжений, описывающую установленное состояние ЭЭС, можно записать так
=
(1)
Собственные элементы Yii должны включать в себя проводимости нагрузочных и генерирующих ветвей, если они есть в узле i.
Для системы уравнений выполним прямой ход методом Гауса, исключая напряжения узлов до N-1 включительно.
В результате уравнения для узла N будут выглядеть так
и
-
элементы матрицы Y
, преобразованные в процессе исключения.
Уравнения представляют собой баланс токов в узле N. Его можно записать в форме баланса мощности
Из этих уравнений следует, что в результате исключения напряжения из системы уравнений узлов из исходной схемы замещения системы, мы пришли к следующей эквивалентной схеме
Эта схема называется звездообразной моделью ЭЭС с центром в узле N.
Для определения предела передаваемой мощности группы источников (в частности одного) схему звезды представим в виде
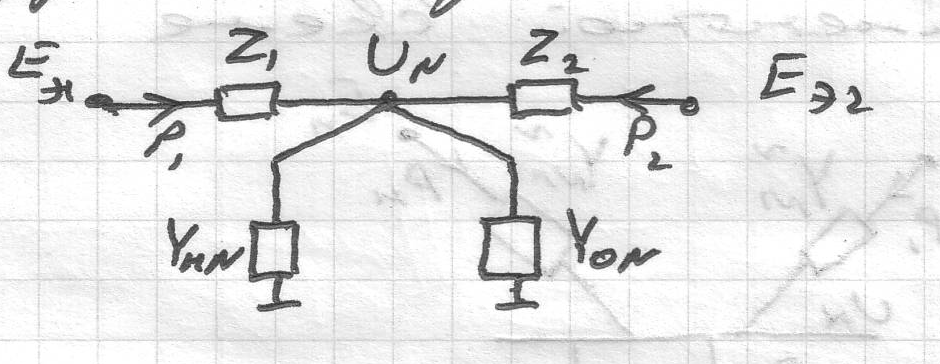
Гк – множество генераторов, отнесенных к к-ой группе
Характеристика мощности первой группы генераторов
Предел передаваемой мощности
Аналогично определяется предел передаваемой мощности для второй группы генераторов.
6. Определение критических напряжений узлов нагрузок сложной ээс путем преобразования исходной схемы к звездообразной.
Выполним расчет планового установившегося режима, приведем исходную схему ЭЭС к звездообразной
Пусть в начале были пронумерованные узлы с ЭДС 1…n, а затем прочие узлы n+1…N, тогда считая ЭДС известными системными уравнениями узловых напряжений, описывающую установленное состояние ЭЭС, можно записать так
=
(1)
Собственные элементы Yii должны включать в себя проводимости нагрузочных и генерирующих ветвей, если они есть в узле i.
Для системы уравнений выполним прямой ход методом Гауса, исключая напряжения узлов до N-1 включительно.
В результате уравнения для узла N будут выглядеть так
и - элементы матрицы Y , преобразованные в процессе исключения.
Уравнения представляют собой баланс токов в узле N. Его можно записать в форме баланса мощности
Из этих уравнений следует, что в результате исключения напряжения из системы уравнений узлов из исходной схемы замещения системы, мы пришли к следующей эквивалентной схеме
Эта схема называется звездообразной моделью ЭЭС с центром в узле N.
Запишем
-
-
=
т.е. схему звезды приведем к виду
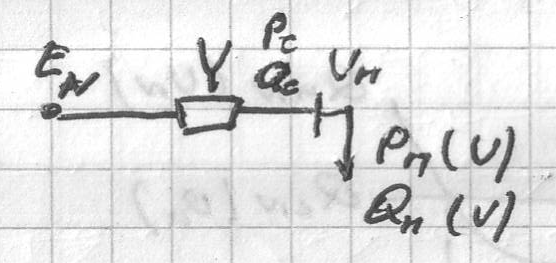
Теперь
для определения Uкр
можно использовать критерий
При
использовании критерия
порядок расчета будет следующим:
- задаются модулем напряжение узла N (UN)
- по статической характеристике PnN (UN) определяется PnN
-
из выражения
определяется δ
- определяется реактивная мощность Qc, поступающая из схемы в узел
- задается новым уровнем напряжение в узле N и расчеты повторяем
По результатам расчета можно построить зависимость
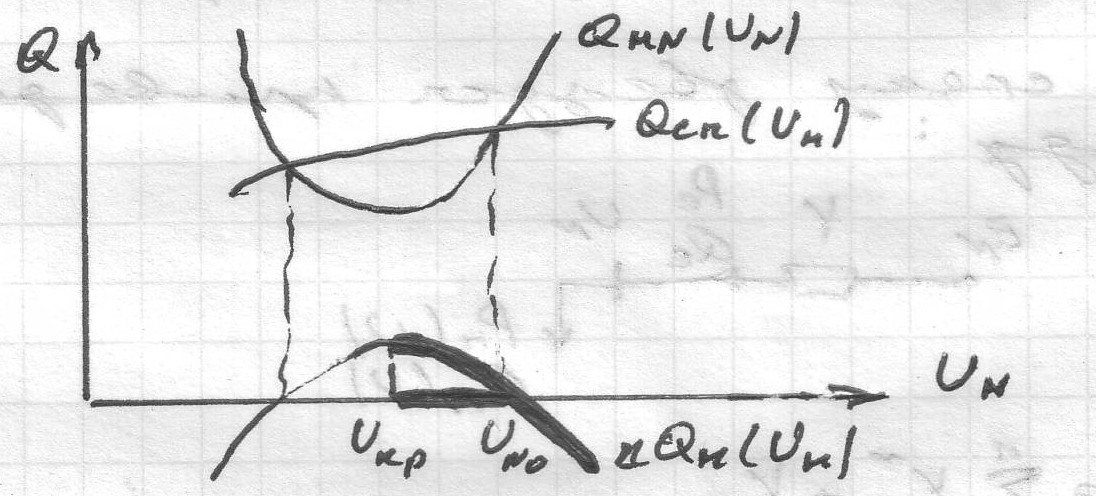
и
определяем Uкр,
соотв. максимуму этой зависимости когда
