3.11. Сравнение электромагнитов постоянного

И ПЕРЕМЕННОГО ТОКОВ

Как сделать выбор между электромагнитом переменного тока и постоянного тока, т.е. с встроенным выпрямителем?

Рассмотрим некоторые параметры электромагнитов.

Сила тяги. При заданной площади сечения полюсов, образующей рабочий воздушный зазор, средняя величина силы в электромагните переменного тока будет вдвое меньше, чем сила в электромагните постоянного тока. Следовательно, использование железа в электромагните переменного тока в 2 раза хуже, чем на постоянном токе.

Вес. При заданных силе тяги и ходе якоря электромагнит переменного тока получается значительно большего веса, чем на постоянном токе.

Влияние вихревых токов. Потери на вихревые токи, а также на перемагничивание увеличивают потребление энергии электромагнитом и его нагрев.

Быстродействие. Электромагниты переменного тока принципиально более быстродействующие, чем постоянного тока.

Область применения. В стационарных промышленных установках, питающихся от сети переменного тока (частотой 50 Гц) большой мощности, многие недостатки не имеют значения.

3.12. Магнитная цепь постоянного магнита

Постоянный магнит – это изделие из магнитотвердого матери-ала, которое предварительно намагничено, поэтому является источником магнитного поля.

Рассмотрим получение постоянного магнита на примере торроидального сердечника из магнитотвердого материала(рис.

52, а).

a) б) в)

Рис. 52

Сделаем два тонких радиальных пропила на расстоянии δ, выпиленный кусок остается на месте.

Намотаем на сердечник обмотку, пропустим по ней ток такой, чтобы намагнитить сердечник до насыщения, после отключим ток и снимем обмотку. Сердечник останется намагниченным .

Вынем выпиленный кусок (рис.52,б) Объем намагниченного вещества уменьшается на объем вынутой части, что приведет к уменьшению магнитного потока в теле сердечника.

В воздушном зазоре δ сердечника проходит магнитный поток. Составляющая м.д.с. постоянного магнита, которая проводит поток в этом зазоре, называется свободной м.д.с.

Величина магнитной индукции в зазоре магнита В_δ зависит от соотношения между длиной воздушного зазора δ и длиной ферромагнитной части магнита ℓ_c (см. рис.52 б).

Обозначим: H _δ – напряженность поля в воздушном зазоре; B_м – магнитная индукция в теле магнита ; H _м –напряженность магнитного поля в теле магнита.

Считая известными кривую размагничивания (рис 52, в), величину зазора δ и длину ℓ_с, определим B_м и H_м.

Из закона полного тока можно получить соотношение:

H _м ℓ _с + H _δ δ =0. (59)

Ноль в правой части выражения (59) объясняется тем, что на постоянном магните нет обмотки с током.

Напряженность магнитного поля H_δ =0,8^.10⁶ B_δ ,[А/м].

Если зазор достаточно мал, то можно пренебречь потоками рассеяния, тогда B_м S _м=B_δ S_δ,

где S_м-площадь поперечного сечения сердечника; S_δ -площадь поперечного сечения воздушного зазора. Тогда

B_δ =B_мS_м/S_δ, H_δ =0,8^.10⁶(S_м /S_δ) ^.B _м. (60) Подставим (60) в (59) и получим

H_м = –0,8^.10⁶ (δ /ℓ_c)^.(S_м /S_δ)^.B _м = –NB_м. (61)

В выражении (61) коэффициент N называется размагничивающим фактором.

Для определения H_м и B_м необходимо построить прямую по уравнению (61). В точке A–пересечения прямой с кривой размагничивания находится решение: H_м и B_м (см. рис 52, в).

Если теперь уменьшить воздушный зазор δ, частично заполнив его по длине ℓ_мс куском магнитомягкого материала, то поток в теле магнита возрастет.

Из-за гистерезиса магнитное состояние постоянного магнита будет изменяться не по участку АЕ (см. рис 52,в) кривой размагничивания ,а по нижней ветви частичного цикла.

Для упрощения расчетов заменяют частный цикл прямой линией, соединяющей его вершины. Эта прямая AC называется прямой возврата.

Тангенс угла наклона прямой возврата к оси абсцисс называется коэффициентом возврата, численное значение которого дается в справочниках для магнитов.

Если обозначить длину оставшегося воздушного зазора δ₁,то

δ₁= δ –ℓ _{м с},

а на основании закона полного тока

H_мℓ_c+H_δ1δ₁+ℓ_мсH_мс=0.

Напряженность поля в магнитомягком материале H_мс много меньше напряженности поля в магнитотвердом материале и в воздушном зазоре при одном и том же значении индукции, поэтому слагаемым H_мс ^.ℓ_мс пренебрегаем.

Тогда

H_м = –0,8 ^.10^{-6 . .}В_м[А/м]. (62)

Магнитное состояние постоянного магнита определяется пересечением прямой возврата с прямой по уравнению (62).

Пример 12.

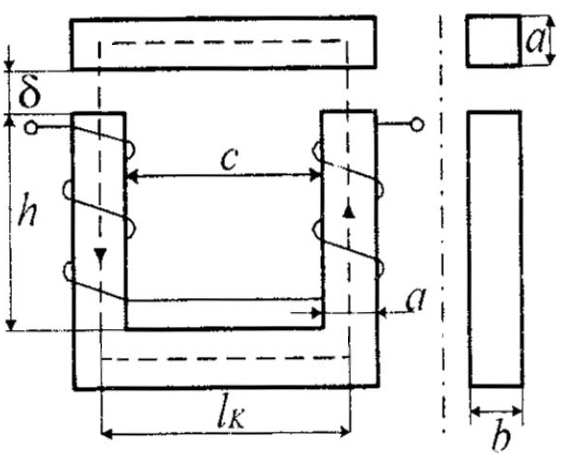
Для приведенной схемы электромагнита (рис. 53) δ = 0,1 мм, Ф_δ =2,5^.10⁴ Вб, а = b = 15мм с = 20 мм, h = 60 мм, материал магнитопровода Э4.Определить намагничивающую силу IW, необходимую для создания заданного рабочего магнитного потока Ф _δ.

Рис. 53