3.8. Определение силы тяги

Рассмотрим процесс возникновения магнитного поля в клапанном электромагните постоянного тока. При включении источника напряжение уравновешивается падением напряжения на активном сопротивлении и э.д.с. самоиндукции:

u(t) = iR + dΨ/dt .

Домножим левую и правую часть выражения на i dt:

u idt = i² Rdt + i dΨ.

Проинтегрируем полученное выражение:

.

Первый интеграл представляет собой энергию, затраченную источником.

Второй интеграл - потери энергии в активном сопротивлении.

Третий интеграл – энергия, затраченная на создание магнитного поля.

Пока сила, развиваемая электромагнитом, меньше силы пружины, якорь электромагнита неподвижен.

Н

i₁

i₂

а рис. 49 представлена зависимость потокосцепления Ψ от тока i, создаю-щего это потокосцепление, при неизменном воздушном зазоре δ₁ и δ₂<δ₁. Как только при Ψ₁ сила элек-тромагнита станет больше силы пружины, так якорь переместится в положение с меньшим воздушным зазором δ₂ < δ₁.

Рис.49

Следовательно, магнитная проницаемость воздушного зазора станет больше, и потокосцепление увеличится, Ψ₂> Ψ₁, а рабочая точка переместится из положения 1 в 2 (см. рис. 49) на кривой Ψ(i) при δ₁ .

Таким образом, за счет изменения магнитной энергии,

которая равна заштрихованной площади S₀₁₂ на рис. 49, якорем электромагнита совершается механическая работа dA.

Для расчета силы, развиваемой электромагнитом, необходимо эту механическую работу разделить на изменение зазора dδ. Причем, сила действует в сторону уменьшения зазора, следовательно, имеет знак минус:

F_ТЯГИ = – dA/ dδ.

Зависимость тяговой силы электромагнита F_T от величины рабочего зазора δ при неизменном значении тока в его обмотке называется статической (тяговой) характеристикой электромагнита.

Если магнитное поле в рабочем зазоре равномерно и

полюсы не насыщенны, то величину силы тяги F_T можно

рассчитать по формуле Максвелла:

F_T = B_mδ²S_δ/(2μ₀). (54)

3.9. РАСЧЕТ МАГНИТНОЙ ЦЕПИ ПЕРЕМЕННОГО

ТОКА

При расчете магнитной цепи переменного тока можно использовать все методы, рассмотренные для постоянного тока, но применять комплексную форму потока , намагничивающей силы , магнитного сопротивления Z_M :

; ; Z_M = R_M + j X_M = Z_M e ^{j(β- α)},

где R_M = ρ_R ℓ / S – активная, X_M = ρ_X ℓ / S – реактивная составляющие магнитного сопротивления, ℓ – длина средней линии магнитопровода, S –площадь поперечного сечения магнитопровода, угол потерь в магнитопроводе

β – α = γ = arctg ρ_X/ ρ_R.

Тогда II закон Кирхгофа в комплексной форме для магнитных цепей, состоящих из N участков и M катушек,

(55)

Mi

Значения ρ_R и ρ_X (удельные магнитные сопротивления) определяются из эмпирических кривых ρ_R(В) и ρ_X(В) [2] для заданного материала магнитопровода.

Рассмотрим последовательную магнитную цепь, в которой проходит один и тот же магнитный поток Ф_m (рис.50).

δ₁

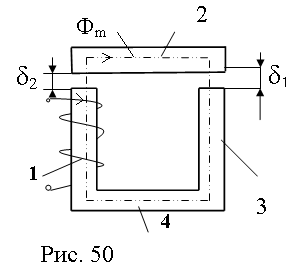
Рис. 50

Магнитная цепь с П-образным магнитопроводом имеет 6 учаcтков: сердечник–1, якорь–2, ярмо–3, основание – 4 и два воздушных зазора δ₁ и δ₂. Комплексное сопрот

1

ивление всей цепи равно сумме комплексных сопротивлений отдельных участков:

Z_M = Z_M1 +Z_M2 +Z_M3+Z_M4 +R_Mδ1+R_Mδ2 =

(ρ_R1 ℓ₁ /S₁+ρ_R2ℓ₂/S₂+ ρ_R3ℓ₃/S₃+ρ_R4ℓ₄/S₄+δ₁/μ₀S_B1

+δ₂/μ₀S_B2)+ j(ρ_X1 ℓ₁ /S₁+ +ρ_X2 ℓ₂ /S₂+ρ_X3ℓ₃/S₃

+ρ_X4ℓ₄/S₄)= R_M + j X_M , (56)

где ℓ_i – длинна средней линии i - го участка;

S_i – поперечное сечение i - го участка.

Решая прямую задачу расчета магнитной цепи, воспользуемся соотношениями (55 и 56).

При заданном магнитном потоке Ф_mi определяем значение магнитной индукции B_mi на каждом участке B_mi =Ф_mi /S_i, а затем по кривым ρ_R(B) и ρ_X(B) определяем соответствующие ρ_Ri и ρ_Xi . После чего вычисляем величину необходимой намагничивающей силы по модулю

. (57)

3.10. ЭЛЕКТРОМАГНИТЫ ПЕРЕМЕННОГО ТОКА

Если магнитный поток создается с помощью обмотки, по которой проходит переменный ток, то такая магнитная система может использоваться в электромагнитах переменного тока.

U

U

Рассмотрим однофазный электромагнит (рис.51).Пусть Ф(t)=Ф_m sin t, где Ф_m = U / (4,44 fW). Тогда из формулы Максвелла (см. 54) можно определить мгновенное значение силы тяги в килограммах.

Рис. 51

F(t) = Ф² /2μ₀S = Ф²_m sin t /2μ₀S=

. (58)

Из (58) следует, что мгновенное значение силы F(t) изменяется от нуля до максимального значения

с частотой, в 2 раза превышающей частоту переменного тока питающей сети.

Первое слагаемое в выражении (58) – среднее значение силы за период, которое используется как расчётное значение полезной силы, действующей на один полюс

.

Второе слагаемое (58) – переменная составляющая силы, которая приводит к вибрации якоря в электромагните, что является отрицательным явлением.

От выражения (58) для силы можно перейти к другому , но учитывая, что в однофазном электромагните 2 полюса (см. рис.51) ,

.

Для снижения вибраций, вызываемых переменной составляющей F(t), применяют расщепление полюса с экранирующей обмоткой или короткозамкнутым витком. В результате получают сглаживание пульсаций магнитного потока.