Алгоритм решения задачи

1. Разбиваем магнитную цепь на участки постоянного сечения и определяем длины их средних линий и площади и поперечных сечений S_k.

2. Исходя из постоянства потока вдоль всей цепи, по заданному потоку и сечению определяем магнитные индукции. Потоками рассеяния пренебрегаем, что возможно при - наименьший размер поперечного сечения магнитопровода. Вк = Ф_K/ S_K .

3. По кривой намагничивания определяем напряженность магнитного поля Нк для ферромагнитных участков магнитной цепи. Напряженность поля в воздушном зазоре находим из ^{соотношения В=} , ^{откуда H воздуха = 0,8.106.В , напряженность Н при этом измеряется в [А/м], а индукция В в [Т].}

4. Составляем уравнение по II закону Кирхгофа и определяем искомую намагничивающую силу

5. Определение магнитного потока в неразветвленной магнитной цепи по заданной намагничивающей силе

В данном случае речь идет о решении обратной задачи.

Дано: геометрические размеры магнитной цепи S_К, ℓ_К; кривая намагничивания В(Н) и намагничивающая сила IW.

Определить: рабочий магнитный поток Ф_δ или индукцию В.

Для решения задачи необходимо построить зависимость потока Ф в функции от намагничивающей силы ∑Н_Кℓ_К = IW, а

затем найти на ней рабочую точку.

Алгоритм расчета.

1. Задаемся значениями: B_δ⁽¹⁾ , B_δ⁽²⁾ , B_δ⁽³⁾ … B_δ⁽ⁿ⁾ .

2. Определяем значения магнитных потоков, Ф_δ⁽¹⁾...Ф_δ⁽ⁿ⁾,

исходя из соотношения Ф⁽ⁿ⁾ = B_δ⁽ⁿ⁾S.

3. Для каждого B_δ⁽ⁿ⁾ определяем намагничивающую силу (∑Н_Кℓ_К)⁽ⁿ⁾ = (IW)⁽ⁿ⁾ по алгоритму предыдущей задачи.

4 . По данным расчета строим зависимость (рис. 45) Ф_δ(∑Н_Кℓ_К)=Ф_δ(IW).

При заданном значении намаг-ничивающей силы (IW)_зад по кривой Ф_δ(IW) определяем Ф_δ, а затем индукцию

B_δ = Ф_δ/S.

Рис. 45

6. Расчет магнитной цепи с учетом магнитного сопротивления и потоков рассеяния

В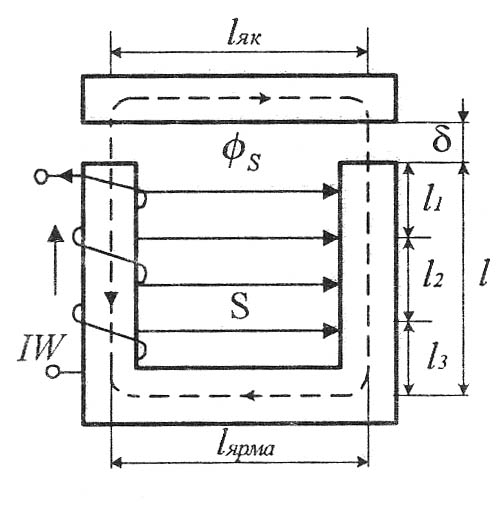 данном параграфе рассмотрим решение прямой задачи при условии, что будем учитывать потоки рассеяния Ф_S.

Пусть заданы геометрические размеры электромагнита постоян-ного тока (рис. 46).

Разобьем длину сердечника на несколько равных участков,

например на три: ℓ₁,ℓ₂,ℓ₃.

Рис.46 Тогда магнитная цепь может быть представлена схемой (рис.47), в которой каждый участок магнитной цепи заменен магнитным сопротивлением: R_δ,R₁₂,R₂₃,R₃₄ , а потоки Ф_δ2, Ф_δ3 - на каждом участке замыкаются через соответствующие магнитные сопротивления: R_S1, R_S2, R_S3. Намагничивающая сила разбита на отдельные источники IW=E=E₁+E₂+E₃ . Причем, E₁ = Eℓ₁/ℓ, E₂ = Eℓ₂/ℓ,

E₃ = Eℓ₃/ℓ.

На основании I и II законов Кирхгофа для магнитных цепей и

учитывая, что магнитное напря-жение воздушного зазора

Рис.47

U_Mδ=Ф_δ/G_δ, где G_δ – магнитная проницаемость воздушного зазора, которая определяется из соотно-шения без учета выпучивания силовых магнитных линий G_δ=μ₀S/δ, из системы уравнений можно рассчитать магнитодвижущую силу Е.