3.3. Магнитная система и магнитная цепь электрических аппаратов

Магнитная система – это совокупность проводников с током (или постоянных магнитов) и элементов из магнитомягких материалов.

Расчет магнитной системы можно сделать либо методами теории поля, либо методами теории цепей.

Методы теории поля, конечно, более точные, но и более трудоемкие.

Методы теории цепей менее точны, так как не учитывают трехмерности магнитных полей, но менее трудоемки, следовательно, решение получаем быстрее.

Магнитная цепь – это упрощенная модель магнитной системы, которая включает в себя такие понятия, как: источники - м.д.с., магнитное напряжение – U_М , магнитный поток Ф, магнитную проводимость G_М, магнитное сопро-тивление R_M.

Вводится аналогия с электрической цепью (схемой):

э.д.с. – соответствует м.д.с.;

току – магнитный поток Ф;

электрическому напряжению – магнитное напряжение между любыми двумя точками магнитной цепи 1 и 2 U_M, которое определяется из соотношения:

электрическому сопротивлению – магнитное сопротив-ление R_M;

электрической проводимости – магнитная проводимость G_М.

Тогда можно сформулировать законы Кирхгофа для магнитных цепей.

I закон Кирхгофа

Алгебраическая сумма магнитных потоков в любом узле магнитной цепи равна нулю:

. (44)

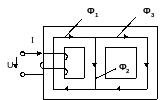
Рис. 42

Первый закон Кирхгофа для магнитной цепи вытекает из условия непрерывности линий магнитной индукции.

Например, для магнитной цепи, изображенной на рис. 42, можно записать уравнение по I закону Кирхгофа

Ф₁ – Ф₂ – Ф₃ = 0.

Ток, проходящий по катушке, создает магнитный поток Ф₁, который, проходя по магнитопроводу, расходится на два потока Ф₂ и Ф₃ .

II закон Кирхгофа

Алгебраическая сумма магнитных напряжений на маг-нитных сопротивлениях любого произвольного замкнутого контура равна алгебраической сумме м.д.с., действующих в этом контуре:

(45)

.

II закон Кирхгофа вытекает из закона полного тока. Учитывая, что м.Д.С. F определяется через ток I и число витков w, ,

II закон Кирхгофа можно записать в другой форме:

^.

Законы Кирхгофа справедливы для линейных и нелинейных цепей.

Закон Ома для магнитной цепи.

Участок магнитной цепи называется линейным, если магнитная проницаемость его постоянна, = const.

Рассмотрим такой участок линейной магнитной цепи, длина которого равна ℓ, а площадь поперечного сечения S.

Справедливо соотношение:

.

Следовательно, ,

где магнитное сопротивление участка цепи,

тогда магнитная проводимость.

Если обозначить удельное магнитное сопротивление материала , то магнитное сопротивление тогда можно вычислить из соотношения

. (46)

3.4. Методы расчета магнитных цепей

Существуют две задачи расчета магнитных цепей: прямая и обратная.

Прямая задача: задан магнитный поток Ф (или магнитная индукция В) на некотором участке магнитной цепи, необходимо определить м.д.с. F, необходимую для создания данного магнитного потока.

Обратная задача: необходимо определить величину магнитного потока Ф по известной м.д.с. F.

Как для прямой, так и для обратной задач известны все геометрические размеры магнитной системы и материал магнитопровода.

Расчет магнитной цепи делают на постоянном или переменном (гармоническом) токе, а также с постоянными магнитами.

Кроме того, модель магнитной цепи для заданной магнитной системы может учитывать поток рассеяния, а может не учитывать (в первом приближении расчета). Рассмотрим магнитную систему прямоходового электро- магнита постоянного тока (рис. 43):

1 ‑ якорь, или подвижная часть магнитной цепи;

2 ‑ намагничивающая катушка;

3 – сердечник ‑ часть магнитной цепи, на которой находится катушка;

4 ‑ корпус, или ярмо;

δ ‑ воздушный зазор, называе-мый рабочим.

Рис. 43

Ярмо, сердечник и якорь электромагнита выполнены из электротехнической стали.

При подаче в обмотку тока якорь притягивается к сердечнику электромагнитным усилием, вызванным взаимодействием микротоков в якоре и сердечнике. В результате воздушный зазор уменьшается и происходит преобразование электромагнитной энергии в механическую.

Воздушный зазор , меняющийся при перемещении якоря, называется рабочим. Соответственно поток, проходящий через рабочий зазор, называется рабочим потоком Ф .

Все остальные потоки в магнитной цепи называются потоками рассеяния Ф_S. Сила, развиваемая якорем электромагнита, определяется в основном потоком Ф в рабочем зазоре.

Рассмотрим решение прямой задачи расчета электромагнита без учета потоков рассеяния, т.е. в первом приближении (рис. 44).

П

Фякоря

Рис. 44

ри решении прямой задачи задано: конфигурация и геоме-трические размеры магнитной цепи, кривая намагничивания ферромагнитного материала сер-дечника, магнитный поток или индукция в каком-либо сечении

магнитопровода.

Необходимо определить: намагничивающую силу или число витков намагничивающей обмотки.