
- •2. Содержание теоретического курса
- •3. Основная и дополнительная литература
- •3.1.Основная литература
- •3.2.Дополнительная литература
- •4. Практические занятия
- •6. Индивидуальные занятия
- •7. Самостоятельная работа
- •Часть I конспекта охватывает первый модуль (из двух) обучения по курсу. По мнению автора, эта часть является основополагающей для понимания всех процессов, связанных с аппаратами.
- •Введение
- •Основные физические явления и процессы в электрических аппаратах
- •1. Тепловые процессы в электрических аппаратах
- •1.1. Источники теплоты в электрических аппаратах
- •1.2. Способы распространения теплоты в электрических аппаратах
- •1.3. Задачи тепловых расчетов
- •1.4. Режимы нагрева электрических аппаратов
- •1.5. Термическая стойкость электрических аппаратов
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Решение.
- •Контрольные вопросы
- •Контактная система электрических аппаратов
- •Классификация электрических контактов
- •Контактная поверхность и контактное сопротивление
- •Нагрев контактов
- •2.4. Режимы работы контактов
- •2.5. Материалы контактов
- •Решение.
- •Решение.
- •Контрольные вопросы
- •3. Электромагнитные явления в электрических аппаратах
- •3.1. Основные понятия теории ферромагнетизма
- •Закон электромагнитной индукции
- •3.2. Кривые намагничивания и петли гистерезиса. Магнитные материалы
- •Динамические петли гистерезиса
- •3.3. Магнитная система и магнитная цепь электрических аппаратов
- •I закон Кирхгофа
- •II закон Кирхгофа
- •II закон Кирхгофа вытекает из закона полного тока. Учитывая, что м.Д.С. F определяется через ток I и число витков w, ,
- •3.4. Методы расчета магнитных цепей
- •Алгоритм решения задачи
- •Определение магнитного потока в неразветвленной магнитной цепи по заданной намагничивающей силе
- •Расчет магнитной цепи с учетом магнитного сопротивления и потоков рассеяния
- •3.7. Расчёт катушки электромагнита
- •3.8. Определение силы тяги
- •3.11. Сравнение электромагнитов постоянного
- •3.12. Магнитная цепь постоянного магнита
- •Решение.
- •Решение.
- •Контрольные вопросы
- •4. Электродинамическая стойкость электрических аппаратов. Расчет электродинамических усилий
- •Пример 14.
- •Решение.
- •Пример 15.
- •П ример 16.
- •Решение.
- •Пример 17.
- •Решение.
- •Контрольные вопросы
- •5. Электрическая дуга и дугогасительные системы
- •5.1. Электрическая дуга в цепи постоянного тока
- •5.2. Дугогасительные системы
- •5.3. Дугогасительные камеры
- •Приложения
- •Медный эмалированный провод пэв-1
- •Продолжение таблицы п.4
- •Часть I
Решение.
Уравнение
кривой нагрева в простейшем случае
имеет вид
 ,
,
где
 ‑ установившееся превышение
температуры.
‑ установившееся превышение
температуры.
Расчет
уст
и Т сделаем
на единице длины проводника
 .
.
Из уравнения Ньютона (10)
Р=КТSохл(-0)= КТSохлуст,
oткуда
 .
.
Охлаждающая
поверхность при
имеет площадь
 .
.
В свою очередь мощность Р постоянного тока I из (1)
 ,
,
 .
.
Следовательно,
установившееся превышение температуры С.
Постоянная времени нагрева:
С.
Постоянная времени нагрева:
 ,
,
где
 - теплоемкость;
- теплоемкость;
 -
удельная теплоемкость для меди,
-
удельная теплоемкость для меди,

 ;
;
 ‑
масса стержня длиной в 1 м;
‑
масса стержня длиной в 1 м;
 -
плотность меди
-
плотность меди

 ;
;
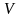 -
объем проводника
-
объем проводника
 ;
;
 -
охлаждающая поверхность.
-
охлаждающая поверхность.

Таким образом, уравнение кривой нагрева:

Для построения рассмотрим две точки (рис.17):
п ри
ри

 ;
;
при
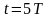
 .
.
5Т- это время, в
течение которого переходный процесс нагрева практически закончится.
Рис. 17
Пример 6.
Найти
конечную температуру медного круглого
проводника диаметром
 ,
который в течение 1,5 с нагружается током
,
который в течение 1,5 с нагружается током
 или (3000*N),
если в начальный момент времени проводник
находился в спокойном воздухе при
температуре
или (3000*N),
если в начальный момент времени проводник
находился в спокойном воздухе при
температуре
 ,
а коэффициент теплоотдачи с его
поверхности
,
а коэффициент теплоотдачи с его
поверхности

 .
.
Решение.
Постоянная времени нагрева:
 ,
,
где
С и
 находим
по таблице П.1 для меди.
находим
по таблице П.1 для меди.
П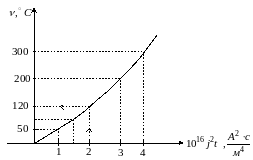 оскольку
оскольку
 ,
процесс можно считать адиабатическим
и температуру проводника определить
по кривой адиабатического нагрева [2]
для меди (рис. 18).
,
процесс можно считать адиабатическим
и температуру проводника определить
по кривой адиабатического нагрева [2]
для меди (рис. 18).
По
условию задачи

Рис. 18
Следовательно,
по кривой
 определим конечную температуру
определим конечную температуру
 .
.
Пример 7.
Решить
пример по условиям предыдущего, но
считать, что в начальный момент времени
проводник был нагрет до температуры
 .
.
Решение.
Для температуры квадратичный импульс плотности тока определим по кривой (рис. 19).

Следовательно, конечный квадратичный импульс плотности тока:

По
кривой адиабатического нагрева (см.
рис. 19) для
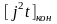 находим
находим
 .
.

Пример 8.
Определить
необходимый диаметр поперечного сечения
круглой проволоки нихромового элемента
сопротивления реостата, если известно,
что в момент времени, когда элемент
сопротивления нагреется до температуры
 ,
через него в течение времени
,
через него в течение времени
 проходит ток
проходит ток
 (или 10*N).
Допустимая температура нагрева нихрома
в кратковременном режиме
(или 10*N).
Допустимая температура нагрева нихрома
в кратковременном режиме
 .
.
Решение.
По кривой адиабатического нагрева для нихрома [2], изображенной на рис. 20, определим конечный, или суммарный квадратичный импульс плотности тока при допустимой температуре
 ,
,
при
 .
.

Рис. 20
Допустимый квадратичный импульс плотности тока:
 Учитывая,
что плотность тока
Учитывая,
что плотность тока

где
 - проходящий ток,
- проходящий ток,
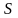 -
площадь поперечного сечения проводника,
-
площадь поперечного сечения проводника,
 ,
,
следовательно
 ,
а
,
а
 .
.
Тогда диаметр поперечного сечения в проводнике:
 .
.
Пример 9.
Определить количество теплоты, передаваемое через S=1м2 плоской текстолитовой стенки толщиной =20 мм. Разность температур на поверхностях стенки =30 С (5*N) .
Решение.
Из закона Ома для теплопроводности
 .
.
Тепловое сопротивление плоской стенки без источников теплоты
 .
.
Теплопроводность определим из таблицы П.2 для текстолита

Сечение стенки S=1 м2 (по условию), тогда тепловое сопротивление

Тепловые потери

