3.3.Моделирование элементов деятельности пользователя с использованием модели интеллектуального агента
Рассмотрим для примера моделирование деятельности модели интеллектуального агента.
Содержательный анализ позволяет выявить следующие возможные варианты организации делятельности.
Вариант 1
Студент мотивирован получить оценку 3и имеет в запасе 45 минут директивного времени для изучения учубного модуля. Помимо мотивации и директивного времени, студент имеет такие входные параметры (Табл.8):
Таблица 8 – Входные параметры студента
B1n= |
0,83 |
B1s= |
0,70 |
B1v= |
0,60 |
K11= |
1,00 |
K00= |
0,80 |
M(Xp)n= |
10,00 |
M(Xp)s= |
10,00 |
M(Xp)v= |
10,00 |
D(Xp)= |
1,00 |
M(Xk)= |
4,00 |
D(Xk)= |
0,20 |
Директивное время (минут) = |
45 |
Таблица 9 – Выходные параметры для студента
Показатель |
Модели изучения для низкой мотивации |
|
|||||
1 |
2 |
3 |
4 |
|
|||
Вероятность |
В |
0,571787 |
0,869731147 |
0,960648148 |
0,991873805 |
|
|
В(св) |
1,0000 |
0,3236 |
0,2766 |
0,2081 |
|
||
Временной |
M, c |
30 |
51,71656402 |
48,61111111 |
54,32122371 |
|
|
D, c2 |
3 |
215,4727225 |
37,09705075 |
131,4047922 |
|
||
Исходя из полученных результатов, студенту целесообразно взять первую модель изучения модуля (без самоконтролей). В случае своевременного изучения материала по данной модели (вероятность равняется 100%), студент получит оценку 3 с вероятностью ≈ 57%. Студенту не целесообразно изучать материал по второй модели изучения модуля (которая предусматривает итоговый контроль), так как ему вряд ли хватит времени на изучение материала (вероятность своевременного изучения материала составляет 32%). Если студент все-таки успеет изучить материал вовремя, то вероятность получить оценку 3 заметно повышается (выше на ≈ 35% по сравнению с первой моделью). Вероятность получить оценку 3 увеличивается с каждой моделью в связи с тем, что промежуточные и итоговые контроли обеспечивают лучшее усвоение учебного материала.
Теперь можно произвести наблюдение – сколько же времени нужно выделить студенту, что бы ему было целесообразнее выбрать вторую модель изучения учебного модуля. Построим график зависимости вероятности своевременного изучения модуля от директивного времени студента (Рис.3.6).
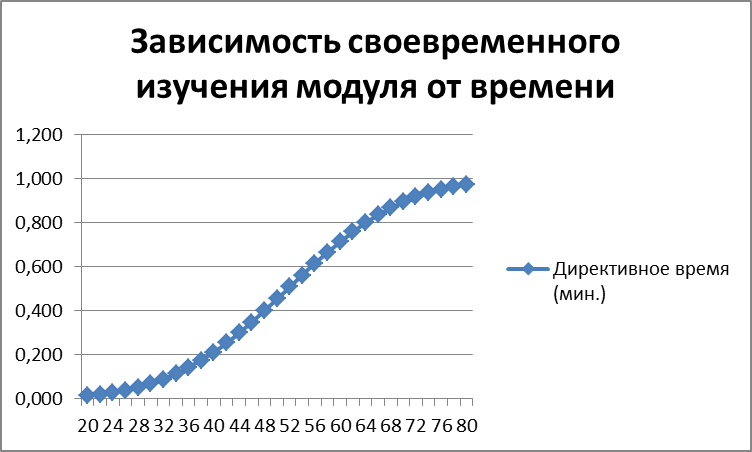
Рисунок 3.6 – Зависимость вероятности своевременного изучения модуля от директивного времени
Исходя из полученных результатов, можно сделать вывод, что студенту необходимо выделить хотя бы 60 минут (на 15 минут больше), что бы целесообразность выбора второго модуля изучения материала была выше, чем первого.
Вариант 2
Необходимо произвести статистический расчет по студентам с разной мотивацией и проследить, как изменяется их математическое ожидание а так же вероятность получить оценку 3, 4 и 5 в зависимости от их мотивации. При этом, всем студентам выделено одинаковое количество директивного времени на изучение всех учебных модулей, соответствующих своей оценке. На изучение модулей на оценку 3 студентам выделено 45 минут, на 4 – 125 минут, на 5 – 250 минут. Для отслеживания статистики будет взято по 3 студента с разной мотивацией (3 с низкой мотивацией, 3 со средней и 3 с высокой).
Помимо директивного времени, студенты имеют следующие входные параметры (Табл.10):
Таблица 10 – входные параметры студентов
9 |
Студент 1 |
Студент 2 |
Студент 3 |
Студент 4 |
Студент 5 |
B1n= |
0,83 |
0,85 |
0,87 |
0,89 |
0,91 |
B1s= |
0,70 |
0,72 |
0,74 |
0,80 |
0,83 |
B1v= |
0,60 |
0,64 |
0,68 |
0,75 |
0,80 |
K11= |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
K00= |
0,80 |
0,80 |
0,80 |
0,80 |
0,80 |
M(Xp)n= |
10,00 |
10,00 |
10,00 |
10,00 |
10,00 |
M(Xp)s= |
10,00 |
10,00 |
10,00 |
10,00 |
10,00 |
M(Xp)v= |
10,00 |
10,00 |
10,00 |
10,00 |
10,00 |
D(Xp)= |
1,00 |
1,00 |
1,00 |
1,00 |
1,00 |
M(Xk)= |
4,00 |
4,00 |
4,00 |
4,00 |
4,00 |
D(Xk)= |
0,20 |
0,20 |
0,20 |
0,20 |
0,20 |
Продолжение таблицы 10.
9 |
Студент 6 |
Студент 7 |
Студент 8 |
Студент 9 |
B1n= |
0,93 |
0,95 |
0,97 |
0,99 |
B1s= |
0,86 |
0,90 |
0,95 |
0,99 |
B1v= |
0,85 |
0,90 |
0,95 |
0,99 |
K11= |
1,00 |
1,00 |
1,00 |
1,00 |
K00= |
0,80 |
0,80 |
0,80 |
0,80 |
M(Xp)n= |
10,00 |
10,00 |
10,00 |
10,00 |
M(Xp)s= |
10,00 |
10,00 |
10,00 |
10,00 |
M(Xp)v= |
10,00 |
10,00 |
10,00 |
10,00 |
D(Xp)= |
1,00 |
1,00 |
1,00 |
1,00 |
M(Xk)= |
4,00 |
4,00 |
4,00 |
4,00 |
D(Xk)= |
0,20 |
0,20 |
0,20 |
0,20 |
Для начала проведем общий расчет параметров (Табл.11, Табл.12, Табл.13):
Таблица 11 – расчитанные параметры для студентов по моделям изучения модулей на оценку 3
Студенты |
Параметры |
Модели изучения для низкой мотивации |
|||
|
|
||||
1 |
2 |
3 |
4 |
||
Студент 1 |
B |
0,571787 |
0,869731 |
0,960648 |
0,991874 |
M |
30 |
51,71656 |
48,61111 |
54,32122 |
|
D |
3 |
215,4727 |
37,09705 |
131,4048 |
|
B(св) |
1,0000 |
0,3236 |
0,2766 |
0,2081 |
|
Студент 2 |
B |
0,614125 |
0,888363 |
0,965909 |
0,992991 |
M |
30 |
49,1827 |
47,72727 |
53,17757 |
|
D |
3 |
183,7612 |
31,73554 |
109,9542 |
|
B(св) |
1,0000 |
0,3788 |
0,3141 |
0,2177 |
|
Студент 3 |
B |
0,658503 |
0,906028 |
0,970982 |
0,994059 |
M |
30 |
46,78025 |
46,875 |
52,0841 |
|
D |
3 |
154,1557 |
26,72991 |
90,54455 |
|
B(св) |
1,0000 |
0,4430 |
0,3584 |
0,2283 |
|
Студент 4 |
B |
0,704969 |
0,922764 |
0,975877 |
0,995081 |
M |
30 |
44,50406 |
46,05263 |
51,03757 |
|
D |
3 |
126,4955 |
22,05294 |
72,95954 |
|
B(св) |
1,0000 |
0,5176 |
0,4113 |
0,2398 |
|
Студент 5 |
B |
0,753571 |
0,938612 |
0,980603 |
0,99606 |
M |
30 |
42,34877 |
45,25862 |
50,03503 |
|
D |
3 |
100,6341 |
17,67985 |
57,00914 |
|
B(св) |
1,0000 |
0,6042 |
0,4755 |
0,2524 |
|
Студент 6 |
B |
0,804357 |
0,953611 |
0,985169 |
0,996998 |
M |
30 |
40,30893 |
44,49153 |
49,07376 |
|
D |
3 |
76,43814 |
13,58805 |
42,52586 |
|
B(св) |
1,0000 |
0,7042 |
0,5549 |
0,2661 |
|
Студент 7 |
B |
0,857375 |
0,967801 |
0,989583 |
0,997899 |
M |
30 |
38,37905 |
43,75 |
48,15126 |
|
D |
3 |
53,78576 |
9,756944 |
29,36182 |
|
B(св) |
1,0000 |
0,8167 |
0,6555 |
0,2804 |
|
Студент 8 |
B |
0,912673 |
0,981223 |
0,993852 |
0,998764 |
M |
30 |
36,5537 |
43,03279 |
47,26524 |
|
D |
3 |
32,56558 |
6,167697 |
17,38607 |
|
B(св) |
1,0000 |
0,9306 |
0,7859 |
0,2935 |
|
Студент 9 |
B |
0,970299 |
0,993915 |
0,997984 |
0,999596 |
M |
30 |
34,82753 |
42,33871 |
46,41357 |
|
D |
3 |
12,67565 |
2,80307 |
6,482469 |
|
B(св) |
1,0000 |
0,9979 |
0,9440 |
0,2894 |
|
Таблица 12 - расчитанные параметры для студентов по моделям изучения модулей на оценку 4
Студенты |
Параметры |
Модели изучения для средней мотивации |
||||
1 |
2 |
3 |
4 |
5 |
||
Студент 1 |
B |
0,196123 |
0,667506 |
0,909403 |
0,925784 |
0,953403 |
M |
60 |
108,3032 |
153,0007 |
127,6365 |
139,9454 |
|
D |
6 |
440,1715 |
6826,686 |
1493,362 |
14730,23 |
|
B(св) |
1,0000 |
0,7869 |
0,3673 |
0,4728 |
0,4510 |
|
Студент 2 |
B |
0,229221 |
0,698976 |
0,920698 |
0,933609 |
0,958518 |
M |
60 |
104,4084 |
142,7964 |
124,1609 |
135,3497 |
|
D |
6 |
379,1572 |
5410,187 |
1273,98 |
12066,72 |
|
B(св) |
1,0000 |
0,8549 |
0,4044 |
0,5094 |
0,4625 |
|
Студент 3 |
B |
0,266841 |
0,729898 |
0,931089 |
0,941073 |
0,963352 |
M |
60 |
100,6937 |
133,5518 |
120,8762 |
131,0543 |
|
D |
6 |
324,1068 |
4267,756 |
1079,332 |
9824,193 |
|
B(св) |
1,0000 |
0,9115 |
0,4479 |
0,5499 |
0,4756 |
|
Студент 4 |
B |
0,360944 |
0,791853 |
0,950054 |
0,955777 |
0,972745 |
M |
60 |
93,55509 |
117,0451 |
114,5201 |
122,8669 |
|
D |
6 |
226,924 |
2553,713 |
741,0953 |
6232,806 |
|
B(св) |
1,0000 |
0,9816 |
0,5625 |
0,6499 |
0,5108 |
|
Студент 5 |
B |
0,430882 |
0,828326 |
0,960199 |
0,963958 |
0,977898 |
M |
60 |
89,52551 |
108,4151 |
111,0197 |
118,4346 |
|
D |
6 |
177,0667 |
1819,749 |
572,8902 |
4594,134 |
|
B(св) |
1,0000 |
0,9962 |
0,6513 |
0,7204 |
0,5386 |
|
Студент 6 |
B |
0,511616 |
0,863683 |
0,9694 |
0,971685 |
0,982718 |
M |
60 |
85,73062 |
100,7138 |
107,7447 |
114,3346 |
|
D |
6 |
133,4122 |
1256,124 |
428,0794 |
3273,61 |
|
B(св) |
1,0000 |
0,9997 |
0,7534 |
0,7979 |
0,5739 |
|
Студент 7 |
B |
0,625026 |
0,904777 |
0,979385 |
0,980469 |
0,988142 |
M |
60 |
81,44796 |
92,49401 |
104,0602 |
109,7755 |
|
D |
6 |
87,99062 |
747,1799 |
279,8215 |
2017,812 |
|
B(св) |
1,0000 |
1,0000 |
0,8828 |
0,8947 |
0,6327 |
|
Студент 8 |
B |
0,782503 |
0,950581 |
0,989709 |
0,990001 |
0,993964 |
M |
60 |
76,82458 |
84,15152 |
100,1042 |
104,9436 |
|
D |
6 |
43,53038 |
325,4975 |
137,4448 |
913,6293 |
|
B(св) |
1,0000 |
1,0000 |
0,9882 |
0,9831 |
0,7465 |
|
Студент 9 |
B |
0,94148 |
0,987916 |
0,99756 |
0,997577 |
0,998544 |
M |
60 |
73,16478 |
77,91804 |
96,98997 |
101,1861 |
|
D |
6 |
11,7046 |
70,71328 |
37,38346 |
205,32 |
|
B(св) |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
0,9517 |
|
Таблица 13 - расчитанные параметры для студентов по моделям изучения модулей на оценку 5
Студенты |
Параметры |
Модели изучения для высокой мотивации |
||||
1 |
2 |
3 |
4 |
5 |
||
Студент 1 |
B |
0,042363 |
0,385747 |
0,758452 |
0,848772 |
0,900286 |
M |
90 |
150,3508 |
303,4834 |
215,4323 |
249,6336 |
|
D |
9 |
1315,583 |
47846,35 |
3127,419 |
112975,2 |
|
B(св) |
1,0000 |
0,9970 |
0,4034 |
0,7318 |
0,5004 |
|
Студент 2 |
B |
0,060089 |
0,44419 |
0,799835 |
0,868123 |
0,914124 |
M |
90 |
140,2568 |
259,7575 |
204,6745 |
233,2866 |
|
D |
9 |
1069,954 |
31929,14 |
2502,688 |
83214,36 |
|
B(св) |
1,0000 |
0,9996 |
0,4782 |
0,8175 |
0,5231 |
|
Студент 3 |
B |
0,083903 |
0,503679 |
0,835367 |
0,885928 |
0,926558 |
M |
90 |
130,855 |
223,6614 |
195,0039 |
218,9883 |
|
D |
9 |
861,5355 |
21291,77 |
1995,063 |
61030,15 |
|
B(св) |
1,0000 |
1,0000 |
0,5716 |
0,8909 |
0,5499 |
|
Студент 4 |
B |
0,152273 |
0,617171 |
0,889633 |
0,916377 |
0,947187 |
M |
90 |
114,7959 |
171,2406 |
178,9774 |
196,096 |
|
D |
9 |
550,9683 |
9775,148 |
1265,425 |
33085,55 |
|
B(св) |
1,0000 |
1,0000 |
0,7872 |
0,9771 |
0,6165 |
|
Студент 5 |
B |
0,220612 |
0,691224 |
0,917985 |
0,934258 |
0,95894 |
M |
90 |
105,3568 |
145,2322 |
169,8435 |
183,4941 |
|
D |
9 |
395,1677 |
5735,332 |
910,968 |
21449,72 |
|
B(св) |
1,0000 |
1,0000 |
0,9167 |
0,9960 |
0,6751 |
|
Студент 6 |
B |
0,314196 |
0,763344 |
0,941615 |
0,950633 |
0,969478 |
M |
90 |
96,79189 |
124,3308 |
161,658 |
172,4693 |
|
D |
9 |
270,93 |
3261,058 |
630,5578 |
13359,75 |
|
B(св) |
1,0000 |
1,0000 |
0,9861 |
0,9998 |
0,7488 |
|
Студент 7 |
B |
0,455644 |
0,839835 |
0,963259 |
0,967175 |
0,97991 |
M |
90 |
88,27857 |
105,84 |
153,5622 |
161,8115 |
|
D |
9 |
163,5956 |
1623,212 |
387,2102 |
7279,796 |
|
B(св) |
1,0000 |
1,0000 |
0,9998 |
1,0000 |
0,8493 |
|
Студент 8 |
B |
0,670899 |
0,919258 |
0,982736 |
0,983692 |
0,990118 |
M |
90 |
79,96979 |
89,76828 |
145,6491 |
151,6273 |
|
D |
9 |
74,37003 |
600,2399 |
181,2772 |
2937,191 |
|
B(св) |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
0,9652 |
|
Студент 9 |
B |
0,913517 |
0,981857 |
0,996318 |
0,996365 |
0,997814 |
M |
90 |
73,75242 |
78,8976 |
139,6907 |
144,1097 |
|
D |
9 |
17,63843 |
108,4533 |
46,52549 |
561,623 |
|
B(св) |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
|
Теперь построим соответствующие графики, на которых мы будем наблюдать изменение вероятности получить каждую из оценок по каждому из модулей (Рис.3.7 – Рис.3.16):
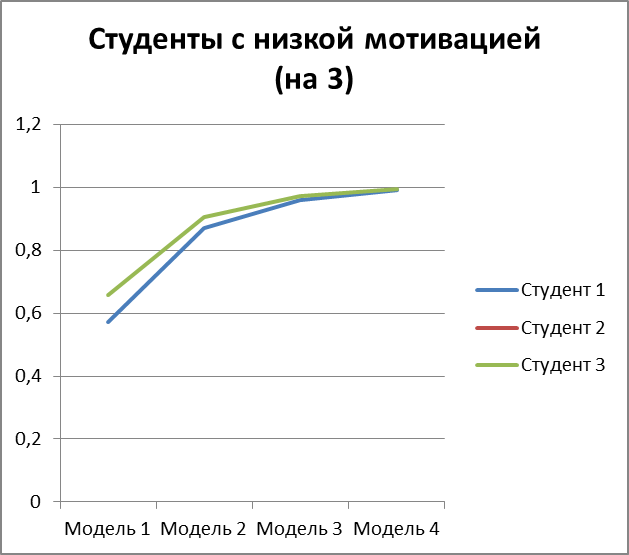
Рисунок 3.7 – вероятность получить оценку 3 для 3 студентов с низкой мотивацией.
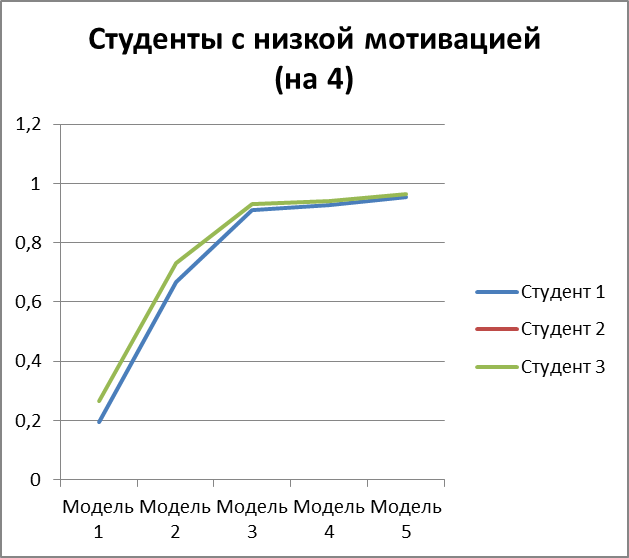
Рисунок 3.8 – вероятность получить оценку 4 для 3 студентов с низкой мотивацией.
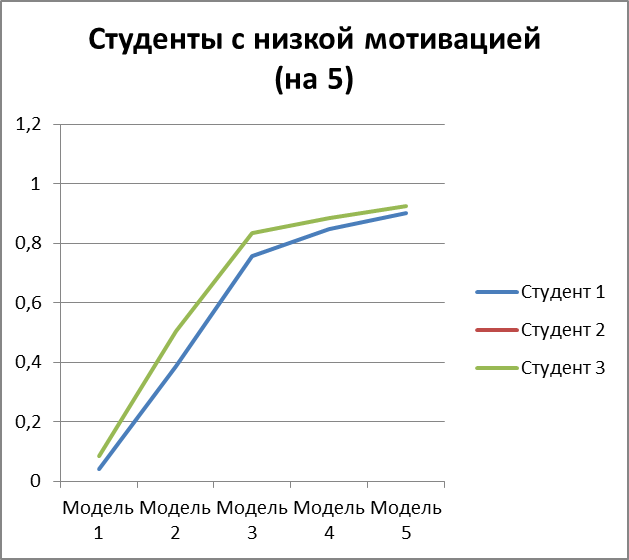
Рисунок 3.9 – вероятность получить оценку 5 для 3 студентов с низкой мотивацией.
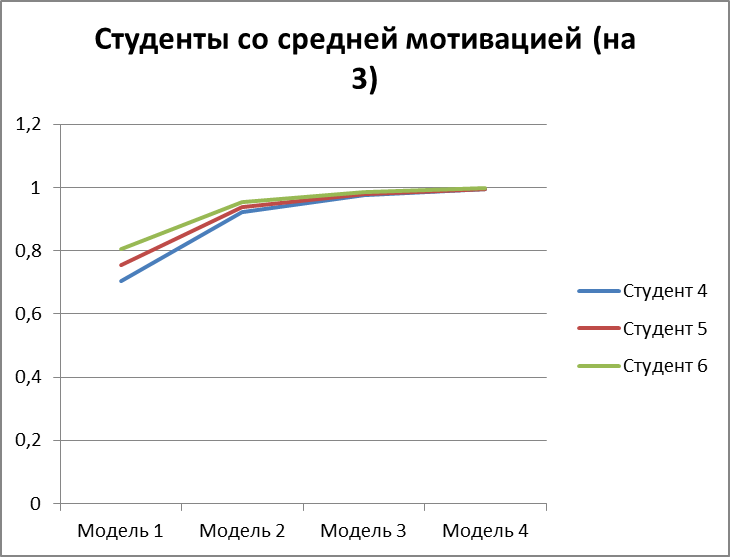
Рисунок 3.10 – вероятность получить оценку 3 для 3 студентов со средней мотивацией.
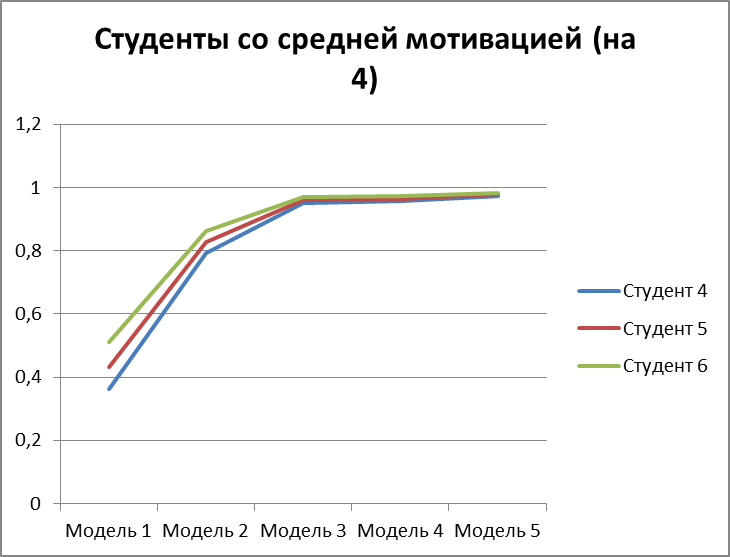
Рисунок 3.11 – вероятность получить оценку 4 для 3 студентов со средней мотивацией.
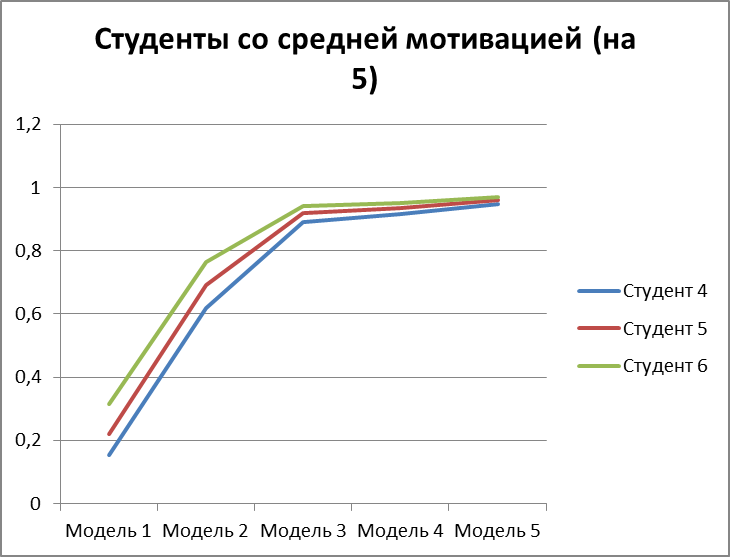
Рисунок 3.12 – вероятность получить оценку 5 для 3 студентов со средней мотивацией.
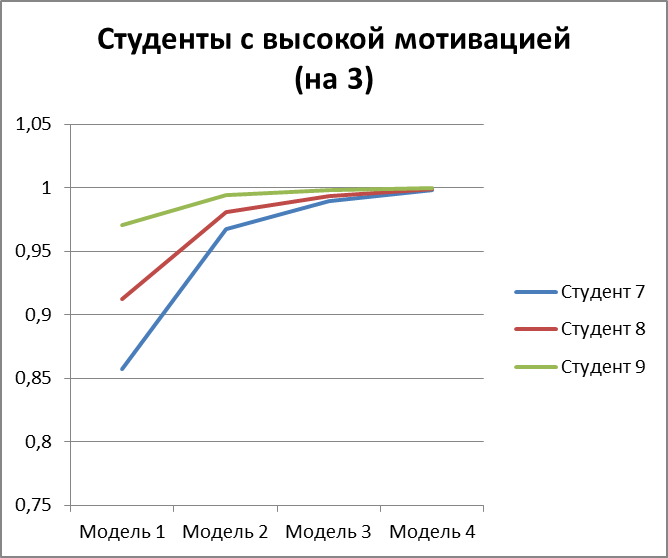
Рисунок 3.13 – вероятность получить оценку 3 для 3 студентов с высокой мотивацией.
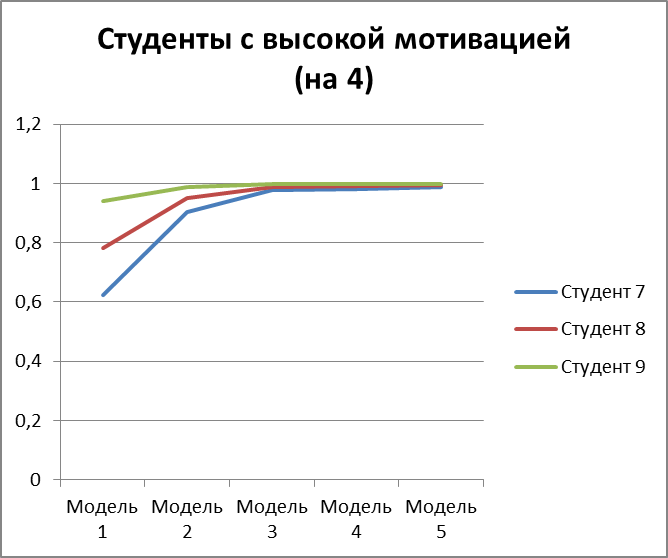
Рисунок 3.14 – вероятность получить оценку 4 для 3 студентов с высокой мотивацией
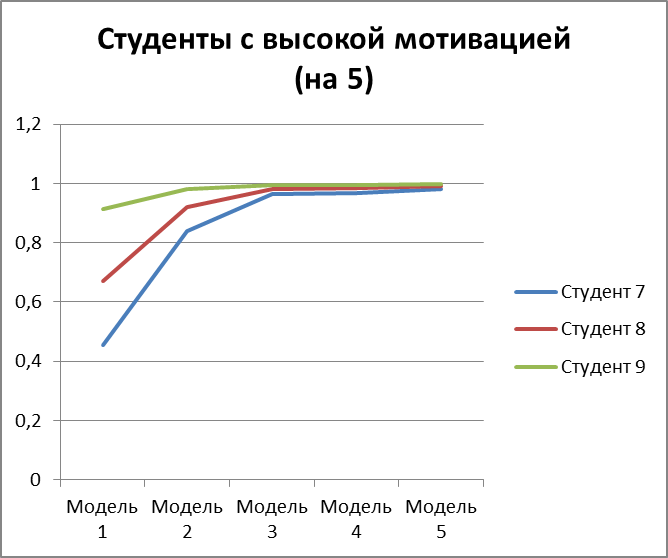
Рисунок 3.15 – вероятность получить оценку 5 для 3 студентов с высокой мотивацией
Теперь построим соответствующие графики, на которых мы будем наблюдать изменение математического ожидания по каждому из модулей (Рис.3.15 – Рис.3.24):
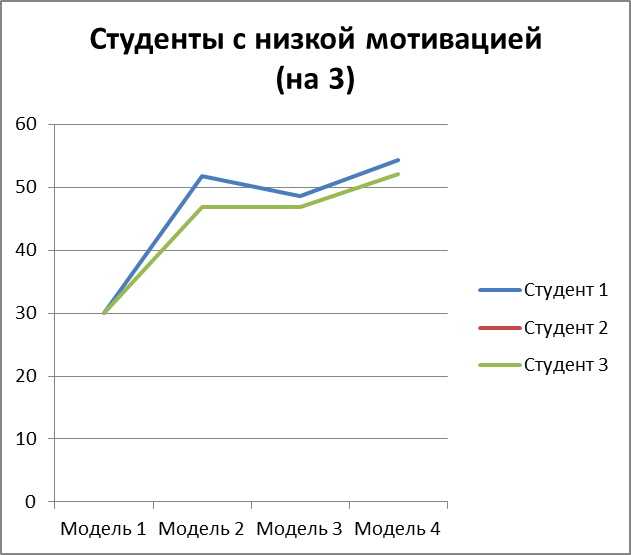
Рисунок 3.16 – мат. ожидание изучения модулей по каждой из моделей для 3 студентов с низкой мотивацией на оценку 3
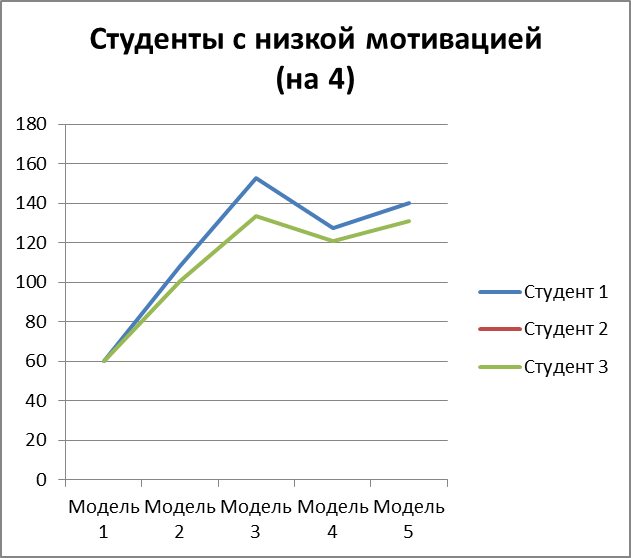
Рисунок 3.17 – мат. ожидание изучения модулей по каждой из моделей для 3 студентов с низкой мотивацией на оценку 4
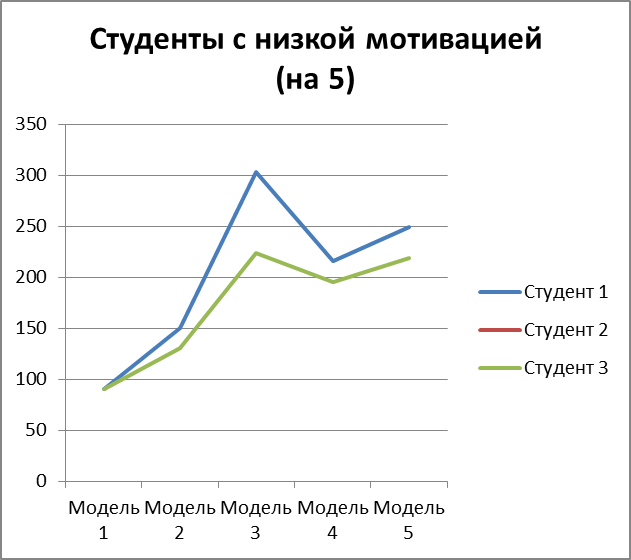
Рисунок 3.18 – мат. ожидание изучения модулей по каждой из моделей для 3 студентов с низкой мотивацией на оценку 5
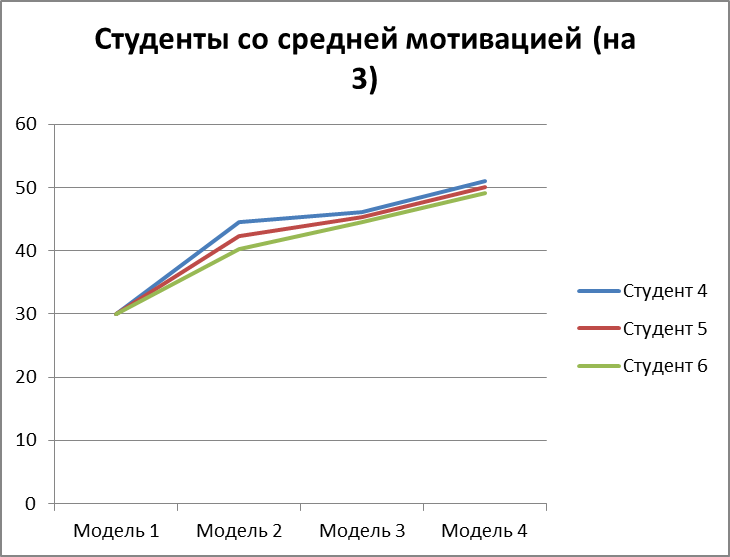
Рисунок 3.19 – мат. ожидание изучения модулей по каждой из моделей для 3 студентов со средней мотивацией на оценку 3
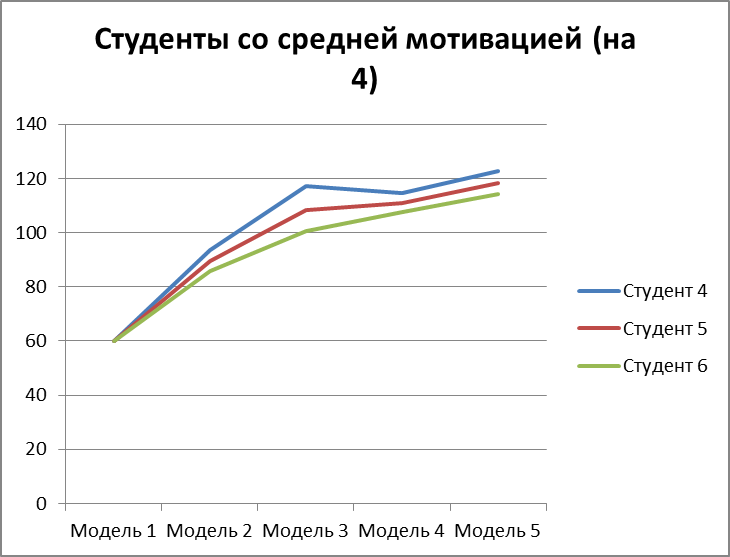
Рисунок 3.20 – мат. ожидание изучения модулей по каждой из моделей для 3 студентов со средней мотивацией на оценку 4
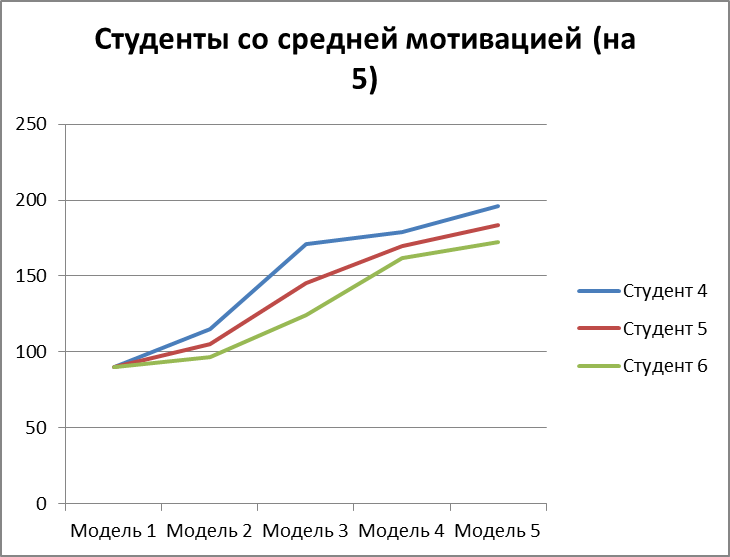
Рисунок 3.21 – мат. ожидание изучения модулей по каждой из моделей для 3 студентов со средней мотивацией на оценку 5
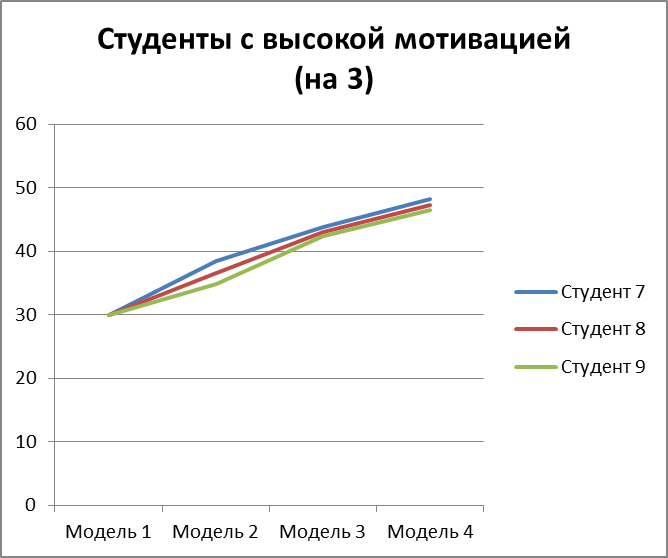
Рисунок 3.22 – мат. ожидание изучения модулей по каждой из моделей для 3 студентов с высокой мотивацией на оценку 3
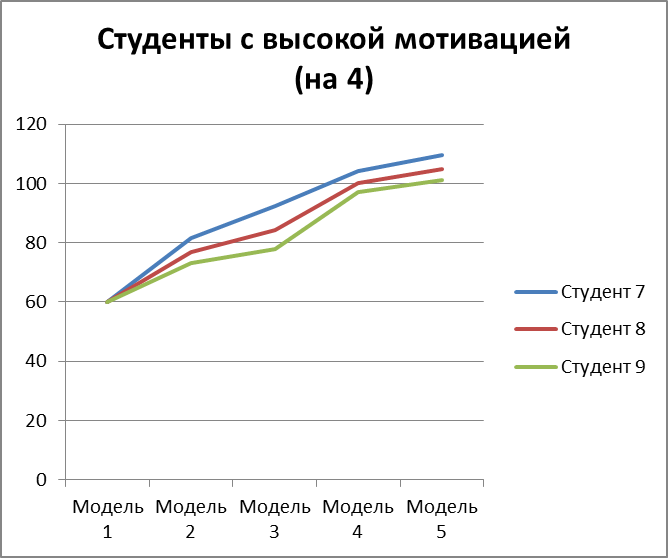
Рисунок 3.23 – мат. ожидание изучения модулей по каждой из моделей для 3 студентов с высокой мотивацией на оценку 4
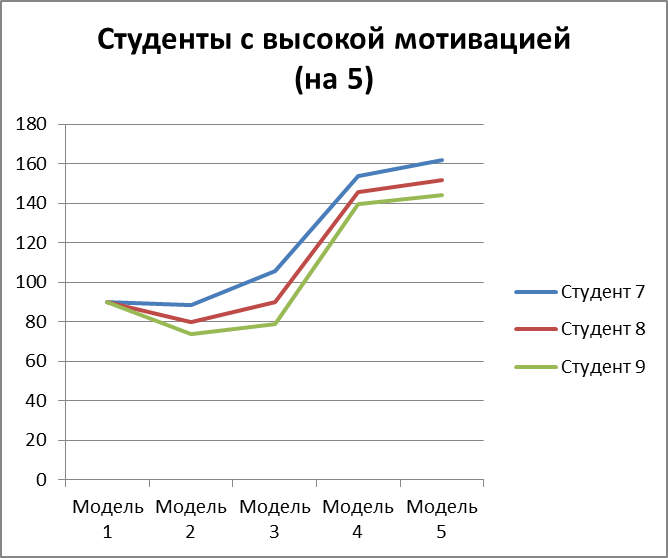
Рисунок 3.24 – мат. ожидание изучения модулей по каждой из моделей для 3 студентов с высокой мотивацией на оценку 5
Из полученных результатов можно сделать вывод, что чем выше мотивация студента – тем выше вероятность получить желаемую оценку не зависимо от модели изучения модуля. Так же, с повышением мотивации студента снижается математическое ожидание изучения модуля любой сложности.
Выводы
Эффективным аппаратом моделирования деятельности интеллектуального агента может быть аппарат функциональных сетей проф. Губинского А.И.
Компьютерно ориентированое описание деятельности студента целесообразно осуществлять с использованием языка описания функциональных сетей, которую предложила Пасько Н.Б.
Разработанная технология, основанная на использованние Excel и VBA, позволяет моделировать деятельность интеллектуального агента.
Проведенное тестовое моделирование подтверждает достоверность результатов, полученных с помощью программного комплекса.