5.2 Вільні коливання в коливальному контурі без активного опору

2.1. Коливальний контур

- утворюється контур, який може коливатися за рахунок накопиченому в ньому енергії.

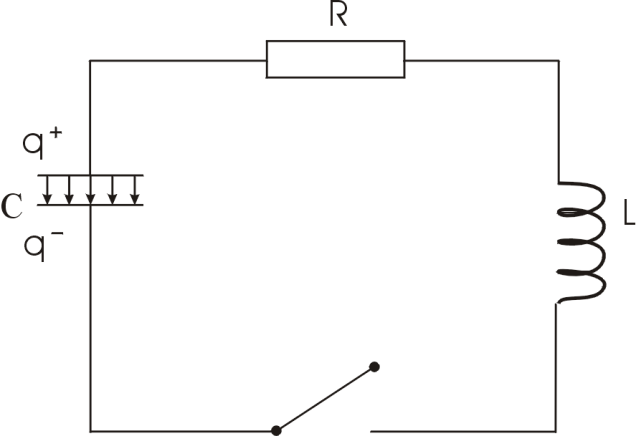
- струму немає

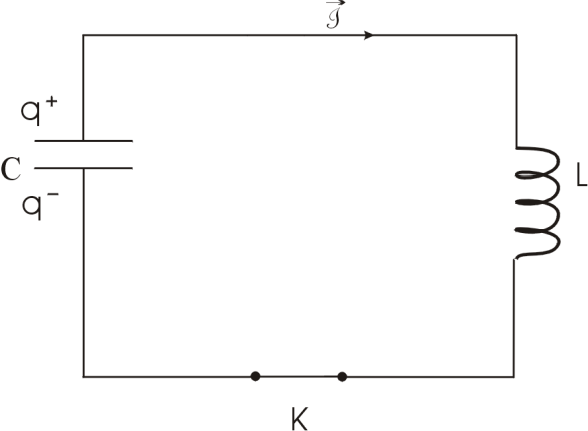
Замикаємо ключ:

Величини, які змінюються:

Коливання вільні, оскільки вони відбуваються за рахунок енергії накопиченої в самому контурі, і не зазнають зовнішнього впливу.

5.3 Вільні загасаючі коливання

3.1. Рівняння вільні коливань в контурі з активним опором.

коефіцієнт загасання;

частота загасаючих коливань.

-(11.6) рівняння вільних загасаючих коливань.

(11.7) –

розв‘язок диференційного рівняння (11.6) за умови слабкого затухання.

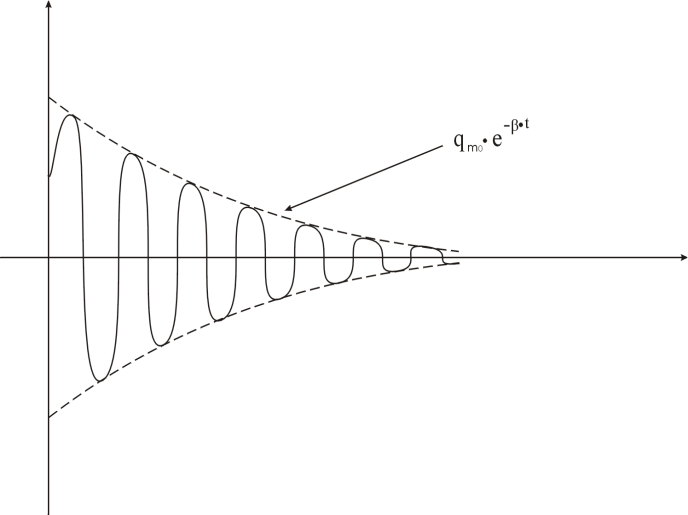
Сила струму випереджає за фазою напругу на конденсаторі на .

5.4 Вимушені електричні коливання

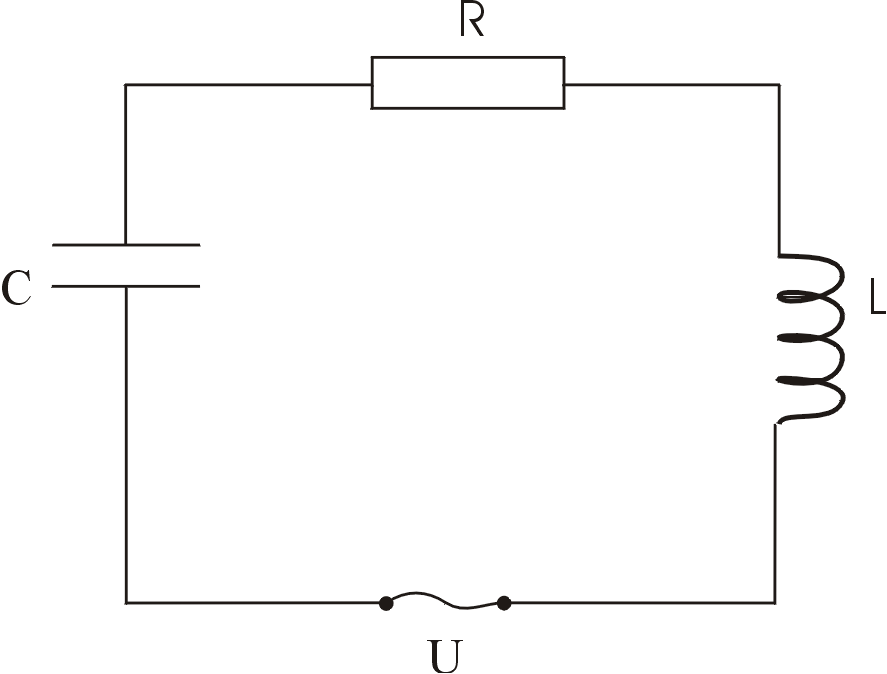
; (11.7)

; (11.8)

(11.9)

Розв’язок рівняння (11.9) є сумою загального розв’язку відповідного однорідного рівняння та частинного розв’язку неоднорідного.

Загальний розв’язок однорідного рівняння містить множник , тобто амплітуда зменшується, коливання загасають. Нас цікавлять усталені коливання, тобто частинний розв’язок рівняння (11.9).

6.1 Процес поширення змінного електромагнітного поля в просторі з плином часу називають електромагнітною хвилею. Максвелл показав, що швидкість поширення електромагнітної хвилі є величиною скінченною і у вакуумі дорівнює швидкості світла (тобто c   3·10⁸ м/с). Електромагнітні хвилі є поперечними, оскільки в кожній точці простору електрична напруженість , магнітна індукція і швидкість поширення цих хвиль взаємно перпендикулярні (рис.5.2.16). Із теорії Максвелла випливає, що швидкість поширення електромагнітної хвилі у речовині визначається за формулою

,                    (5.2.7)

де c - швидкість електромагнітних хвиль у вакуумі; e - діелектрична проникність; m - магнітна проникність середовища. Із формули (5.2.7) видно, що швидкість поширення електромагнітної хвилі в середовищі залежить від електричних і магнітних властивостей цього середовища.

Відстань, на яку поширюється електромагнітна хвиля за один період, тобто найкоротша відстань між таким двома точками хвилі, в яких і коливаються в однакових фазах, називають довжиною електромагнітної хвилі і позначають через l. За аналогією з механічними хвилями:  = ln = l /  T, де T - період, n - частота електромагнітних коливань. Із теорії Максвелла випливає, що довільний заряд, що рухається із прискоренням або коливається, випромінює електромагнітні хвилі.

Електромагнітна хвиля поширюється в діелектрику, але ще краще у вакуумі. Наявність прискорення - головна умова випромінювання електромагнітної хвилі.

У вакуумі електромагнітні хвилі досягають найбільшої швидкості - швидкості світла (c = 3·10⁸ м/с). Властивості електромагнітних хвиль найлегше вивчати, використовуючи передавач і приймач, які працюють на сантиметровому діапазоні. Випромінювання і приймання таких хвиль можна зробити спрямованими. Досліди Герца і пізніше проведені експерименти показали, що електромагнітні хвилі мають такі властивості:

1) в однорідному середовищі поширюються рівномірно і прямолінійно;

2) відбиваються діелектриками, а ще краще провідниками, при цьому виконуються закони відбивання хвиль;

3) заломлюються;

4) фокусуються;

5) дають явища дифракції і інтерференції;

6) поляризуються.

Властивості електромагнітних хвиль виявились такими ж, як і властивості хвиль будь-якої іншої природи.

Електромагнітні хвилі мають майже необмежений діапазон частот і довжин хвиль. Шкалу цих хвиль наведено в дод. Весь діапазон поділяють на декілька вузьких ділянок, для яких установлено конкретні межі.

6.2 Хвильове́ рівня́ння — рівняння, яке описує розповсюдження хвиль у просторі.

Хвильове рівняння є зазвичай рівняння другого порядку у часткових похідних гіперболічного типу, хоча існують хвильові рівняння інших порядків та інших типів.

У одномірному випадку хвильове рівняння записується.

де u — невідома функція, яка описує хвилю, x — просторова координата, t — час, s — фазова швидкість поширення хвилі.

Розв'язки

Хвильові рівняння мають багато можливих розв'язків. Реалізація того чи іншого із них залежить від граничних та початкових умов: від того, як хвиля народилася, які перешкоди зустрічає на своєму шляху, тощо.

Загальний розв'язок хвильового рівняння подається суперпозицією функцій типу

де u0 — амплітуда хвилі, k — хвильове число, ω — циклічна частота, — фаза хвилі.

Хвильове число та частота зв'язані між собою дисперсійним співвідношенням

Інші типи хвильових рівнянь

Вільна частка описується у квантовій механіці рівнянням Шредінгера. Це рівняння параболічного типу, проте комплексне.

Дисперсійне співвідношення у ньому зв'язує енергію частки із її хвильовим вектором.

У релятивістській квантовій механіці використовуються рівняння Дірака, рівняння Клейна-Гордона, тощо. Ці рівняння теж описують поширення хвиль, тож належать до групи хвильових рівнянь.

6.3 Досліди Фарадея, які сприяли відкриттю явища електро­магнітної індукції, досить прості і їх легко відтворити.

Приєднаємо до гальванометра довгий гнучкий провідник і помістимо його між полюсами магніту Якщо провідник і магніт нерухомі, струму в провіднику немає. Але варто почати рухати провідник, як гальванометр відразу ж покаже наявність у провіднику струму. Якщо під час руху провідника в одному напрямі стрілка гальваномет­ра відхиляється, наприклад, вправо, то під час руху в зво­ротному напрямі стрілка відхиляється вже вліво, що свідчить про зміну напряму струму в провіднику. Струм у провіднику виникає і тоді, коли магніт переміщається відносно нерухомого провідника.

Під'єднаємо тепер до гальванометра котушку. Коли все­редину цієї котушки вводити або виймати з неї магніт, гальванометр теж покаже виникнення в колі елек­тричного струму. Отже, струм виникає лише під час відносного руху магніту і провідника.

Замкнемо котушку В через гальванометр і вставимо все­редину неї соленоїд А, який можна під'єднати до джерела струму. У момент замикання кола соленоїда стрілка гальванометра відхилиться, тобто під час зміни (виникнен­ня) магнітного поля соленоїда котушкою проходить елект­ричний струм. Однак після встановлення в соленоїді струму магнітне поле перестане змінюватися, струм у котушці зни­кає — стрілка гальванометра встановлюється на нулі.

Тепер розімкнемо коло соленоїда. У разі зникнення стру­му в соленоїді, а разом з ним і його магнітного поля, стрілка гальванометра відхиляється в протилежний бік. Це означає, що в котушці виникає електричний струм, напрям якого протилежний напряму струму, що проходив при замиканні соленоїда. В цих дослідах під час замикання кола соленоїда виникає магнітне поле, а під час розмикання — зникає. У разі таких змін магнітного поля в котушці виникає струм, який називають індукційним.

У коло соленоїда можна увімкнути реостат і ним зміню­вати силу струму в колі. Легко переконатися, що під час зростання сили струму в колі соленоїда у котушці виникає індукційний струм одного напряму, а під час зменшення — струм протилежного напряму. При зміні сили струму в соле­ноїді змінюється і його магнітне поле, і в котушці виникає індукційний струм.

Отже, ми переконалися, що виникнення індукційного струму пов'язане зі змінами магнітного поля, причому причина цих змін не має значення. Магнітне поле може змінюватися з різною швидкістю. На розглянутих вище дослідах неважко переконатися, що сила індукційного стру­му в замкнутому провіднику визначається швидкістю змін магнітного поля (його індукції).

Для виникнення індукційного струму в замкнутому про­віднику має значення не лише зміна магнітного поля. Важ­ливо ще, як індукція цього поля спрямована відносно поверхні, охоплюваної замкнутим провідником (контуром). Якщо в досліді (мал. 1) провідник переміщати вздовж ліній магнітної індукції, то струм у провіднику не виникає. Не виникає індукційний струм і тоді, коли котушка рухається поступально в однорідному магнітному полі вздовж ліній індукції. В цьому легко переконатися, якщо невелику ко­тушку переміщати всередині довгого соленоїда (мал. 4). В той же час просте вмикання і вимикання струму в соленоїді, якщо всередині закріплена котушка, викликає виникнення в ній індукційного струму. Звідси зробимо ще один висновок: причиною виникнення в замкнутому провіднику індукційно­го струму є зміна кількості ліній магнітної індукції, які пронизують площу, обмежену цим контуром. І чим швидше змінюється ця кількість, тим більшої сили виникає струм. У цьому легко переконатися на такому простому досліді.

Візьмемо рамку з великою кількістю витків тонкого і гнучкого дроту. Різко змінимо площу рамки, вміщеної в сильному магнітному полі (мал. 5). Увімкнутий в коло рам­ки гальванометр і в цьому випадку показує наявність елект­ричного струму. Індукція магнітного поля тут постійна.

Змінюється лише площа, обмежена рамкою, внаслідок чого змінюється кількість ліній магнітної індукції, що прони­зують контур. А ви знаєте, що,добуток модуля магнітної індукції В на площу S контуру, перпендикулярної до цієї площі, називається магнітним потоком. Таким чином, мож­на зробити висновок, що під час зміни магнітного потоку че­рез площу, обмежену будь-яким замкнутим провідним конту­ром, в останньому виникає індукційний електричний струм.

6.4 ЕНЕРГІЯ ЕЛЕКТРОМАГНІТНОГО ПОЛЯ - кількісна характеристика ел - магн. взаємодії. Величина Е. е.. п. може бути встановлена ​​на підставі вимірювання роботи, виробленої ел - магн. полем ( Лоренца силою ) над носіями електричні. зарядів. З визначення напруженості електричні. поля Е і індукції магн. поля В слід вираз для роботи р, яку здійснюють над рухомими зарядами в одиничному об'ємі в одиницю часу:

В (1) -Вектор щільності електричні. струму; u _a - швидкість розподіленого просторів. заряду сорту a, що має щільність r _a; підсумовування проводиться по всіх сортах просторів. зарядів (електронні заряди в металах і вакуумі, іонні заряди в газах та електролітах; пов'язані просторів. заряди, що входять до складу нейтральних молекул діелектриків і магнетиків, і т. д.), беруть участь у взаємодії з ел - магн. полем.

Формально з Максвелла рівнянь , застосованих до вакууму (E = D, У = Н-використовується Гаусса система одиниць ), що пов'язують вектори ел - магн. поля Е, D, Н, У сплотностямі електричні. зарядів r і струмів j, слід співвідношення

6.5 Импульс электромагнитного поля, динамическая характеристика поля - количество движения, которым обладает электромагнитное поле в данном объеме. Тела, помещенные в электромагнитное поле, испытывают действие механических сил. Воздействие поля на тело при этом связано с поглощением телом электромагнитных волн или изменением направления их распространения (отражение, рассеяние, преломление). При излучении телом электромагнитных волн, в частности света, импульс тела также меняется. Так как импульс замкнутой материальной системы в результате излучения, поглощения или отражения электромагнитных волн не может измениться (в силу закона сохранения полного импульса системы), то из этого следует, что электромагнитная волна также обладает импульсом. Существование И. э. п. впервые было экспериментально обнаружено в опытах по давлению света (П. Н. Лебедев, 1899).   Из классической теории электромагнитного поля - Максвелла уравнений - следует, что Импульс электромагнитного поля распределен в пространстве с объемной плотностью  - в системе СГС (Гаусса), или  - в системе СИ, где (ЕН) - векторное произведение напряженностей электрического Е и Н полей, численно равное EH sin a, a - угол между E и , с = 3×10¹⁰ см/сек - скорость света в вакууме. Таким образом, вектор плотности Импульс электромагнитного поля g перпендикулярен Е и Н и направлен в сторону поступательного движения правого буравчика, рукоятка которого вращается в направлении от Е к .   В квантовой теории электромагнитного поля (квантовой электродинамике) носителем энергии и импульса поля являются кванты этого поля - фотоны. Фотон частоты n обладает энергией hn и импульсом h n/c, где h - Планка постоянная. Существование импульса у фотона проявляется во многих явлениях. Например, обмен импульсом между электромагнитным полем и частицей имеет место в Комптона эффекте (упругом рассеянии фотонов на электронах).

6.6 Дипольне випромінювання - випромінювання електромагнітних хвиль диполем, величина якого змінюється з часом.

Нерухомі заряди й заряди, які рухаються рівномірно та прямолінійно, не випромінюють електромагнітних хвиль. Для того, щоб заряд випромінював, потрібно, щоб він рухався з прискоренням.

Математичний опис

Найпростіший випромінювач електромагнітних хвиль - це точковий диполь, величина якого змінюється з часом (d = d(t)). На великій віддалі R від диполя (на віддалі, яка набагато перевищує його розміри) напруженість електричного та магнітного полів матиме вигляд

,[1]

де θ - це кут між напрямком до спостерігача та напрямком диполя, c - швидкість світла, E_θ - напруженість електричного поля, яка направлена перпендикулярно до напрямку розповсюдження хвилі й лежить в площині, утвореній напрямком диполя й напрямком до спостерігача, - напруженість магнітного поля, перпендикулярна до напрямку розповсюдження хвилі й до площини диполя.

Вектор Пойнтінга випроміненої електромагнітної хвилі дорівнює

Таким чином, диполь випромінює електромагнітні хвилі не ізотропно, а здебільшого у напрямках перпендикулярних до себе.

Загальна інтенсивність випромінювання

Якщо диполь здійснює гармонічні коливання d = d0cosωt, то усереднений щодо часу потік електромагнітної енергії, випроміненої диполем, дорівнює

Інтенсивність випромінювання дуже швидко зростає із частотою.