1.

1.1 Магні́тне по́ле — особлива форма матерії, за допомогою якої здійснюється взаємодія між рухомими електрично зарядженими частинками.

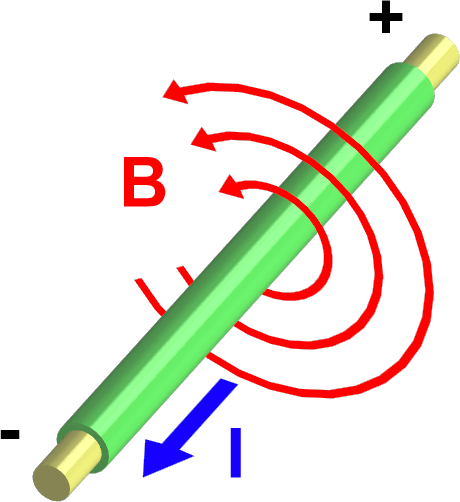
Магнітне поле - складова електромагнітного поля, яка створюється змінним у часі електричним полем, рухомими електричними зарядами або спінами заряджених частинок. Магнітне поле спричиняє силову дію на рухомі електричні заряди. Нерухомі електричні заряди з магнітним полем не взаємодіють, але елементарні частинки з ненульовим спіном, які мають власний магнітний момент, є джерелом магнітного поля і магнітне поле спричиняє на них силову дію, навіть якщо вони перебувають у стані спокою.

Магнітне поле утворюється, наприклад, у просторі довкола провідника, по якому тече струм або довкола постійного магніту.

Магнітне поле є векторним полем, тобто з кожною точкою простору пов'язаний вектор магнітної індукції який характеризує величину і напрям магнітого поля у цій точці і може мінятися з плином часу. Поряд з вектором електромагнітної індукції , магнітне поле також описується вектором напруженості .

У вакуумі ці вектори пропорційні між собою: , де k - константа, що залежить від вибору системи одиниць. В системі СІ, k = μ₀ - так званій магнітній проникності вакууму. Деякі системи одиниць, наприклад СГСГ, побудовані так, щоб вектори індукції та напруженості магнітного поля тотожно дорівнювали один одному: .

Однак у середовищі ці вектори є різними: вектор напруженості описує лише магнітне поле створене рухомими зарядами (струмами) ігноруючи поле створене середовищем, тоді як вектор індукції враховує ще й вплив середовища:

^]

де - вектор намагніченості середовища.

1.3 Магні́тна інду́кція — векторна фізична величина, яка характеризує величину і напрямок магнітного поля з урахуванням впливу середовища. Магнітна індукція пов'язана з напруженістю магнітного поля :

,

де μ— магнітна проникність.

У системі СГС магнітна індукція поля вимірюється в гаусах (Гс), в системі СІ — в теслах (Тл).

1.4 Біо-Савара-Лапласа закон — закон, який визначає напруженість магнітного поля електричного струму, що тече у прямолінійному дуже довгому провіднику.

За законом Біо-Савара

де H — напруженість магнітного поля в точці М на відстані r від прямолінійного провідника із струмом I (мал. 1); k — коефіцієнт пропорційності, величина і розмірність якого залежать від вибору системи одиниць, r — радіусвектор.

Закон Біо-Савара експериментально відкрили 1820 Жан-Батіст Біо і Фелікс Савар. Цей закон є частковим випадком більш загального закону Біо-Савара-Лапласа, сформульованого П. Лапласом 1820 на підставі матеріалів з численних дослідів Ж.-Б. Біо і Ф. Савара.

Мал. 2.

За цим законом величина напруженості магнітного поля в точці М на відстані r від елемента М провідника довільної форми визначається формулою:

де α — кут між напрямом струму I і напрямом радіуса-вектора r (мал. 2). Повна напруженість магнітного поля H, створюваного струмом у провіднику довільної форми і скінченної довжини, дорівнює геометричній сумі елементарних напруженостей.

Наприклад, інтегруванням (2) одержують формули напруженості магнітного поля навколо нескінченно довгого прямолінійного провідника зі струмом, тобто формулу Б. — С. з. (1), напруженість магн. поля в центрі колового струму

напруженість магнітного поля в середній частині дуже довгого соленоїда H = k4πIn та ін. Напрям напруженості магнітного поля в усіх випадках визначається за правилом ґвинта.

1.5 Вихрові поля- вид полів , силові лінії яких ніде не починаються і ніде не закінчуються, вони замикаються самі на себе. Вони названі так через подібність силових ліній у вигляді концентричних кіл із вихром. Розглянемо особливості цих полів. Стаціонарне магнітне поле створюється рухомими зарядами.

Зі шкільного курсу добре відомі силові лінії природних магнітів.Такий же вигляд полів можна отримати, використовуючи замкнутий провідник, по якому тече струм.

Силові лінії утворюють замкнуті криві. Їх напрямок визначається за правилом правого гвинта. Якщо ручку буравчика обертати за напрямком струму у витку, то вістря показує напрям силових ліній. Стаціонарне магнітне поле створюється рухомими зарядами. Напрям силових ліній також можна визначити за допомогою правила гвинта. Для цього треба направити вістря буравчика у напрямку струму, тоді напрямок обертання ручки буравчика співпаде з напрямком силових ліній.

Правило гвинта - мнемонічне правило, що дозволяє просто визначати напрям силових ліній магнітного поля.

Існують суворі закони, що дозволяють визначати величину і напрям силових ліній довільного за формою провідника зі струмом.

Напруженість магнітного поля визначається законом Біо-

Саварра -Лапласа. Ми не будемо розглядати в явному вигляді цей закон. У принципі, з його допомогою можна розрахувати напруженість магнітного поля, створювану будь-яким провідником зі струмом. Так напруженість магнітного поля нескінченно довгого провідника зі струмом на відстані r від нього дорівнює: H = I/2pr.

На достатньо віддаленій відстані від провідника зі струмом магнітне поле можна вважати однорідним. Тобто силові лінії такого поля розташовані паралельно один від одного. На провідник зі струмом, поміщений в однорідне магнітне поле діє сила. Величина сили визначається за законом Ампера.

Для ділянки провідника зі струмом, довжиною L його можна записати в векторному вигляді в системі одиниць СІ як:

F = m0 I [HL] (15.12 )

Тут m0 - постійна, зумовлена вибором системи одиниць (СІ), L-провідник зі струмом I, який задається у векторному вигляді, тому що має напрямок у просторі. Його напрямок збігається з напрямком руху струму, тобто позитивних зарядів.

на провідник зі струмом в однорідному магнітному полі діє сила, спрямована перпендикулярно вектору напруженості магнітного поля H і напряму руху струму (провідника зі струмом L). У цьому полягає принципова відмінність силового впливу вихрового магнітного поля на пробний елемент від поля консервативних сил.

1.6 Скористаємось рівнянням Максвелла для циркуляції вектора напруженості магнітного поля , (1.1) де j – густина струму провідності вільних електричних зарядів;  - струм зміщення, не пов’язаний з наявністю вільних електричних зарядів; Н – напруженість магнітного поля. У провідниках, в яких є вільні електричні заряди, струм зміщення відсутній (він може існувати лише у діелектричному середовищі), тобто . У цьому випадку рівняння (1.1) набуває вигляду: . (1.2) Рівняння (1.2) називається законом повного струму. Для написання закону повного струму через індукцію магнітного поля слід замінити Н у формулі (1.2) на

1.7 Потік і циркуляція магнітного поля

Оскільки на провідник з струмом в магнітному полі діє сила Ампера, то при переміщені провідника в поле на відстанні здійснюється робота A = ( _А ). Нехай провідник довжиною l з струмом I поміщений в однорідне магнітне поле з індукцією , вектор якої направлений перпендикулярно площини рисунка 4.7 від нас. На провідник діє сила Ампера F_A = IlB, під дією якого цей провідник переміщується, паралельно самому собе на відстанні dr. Тоді

A = IbldS , (4.18)

де dS = ldr - площа, описана провідником при своєму русі.

з рис. 4.7 видно, що при цьому вектори , "пронизувють" площину dS (чи "протікають" крізь dS). Вводиться поняття потока вектора магнітной індукції (магнітного потока) через площину dS: элементарним магнітним потоком dФ вектора крізь поверхню площини dS називається скалярная величина, рівна

Рис.4.7.

( 4.14)

де - одиничний вектор зовнішньої нормалі до площини dS. Повний магнітний потік крізь поверхні тоді рівний:

(4.15)

Очевидно, у випадку однорідного магнітного поля Ф = ( ) = Bs·cos , де - кут між направленим вектором магнітной індукції і нормалю до площини . Розмірність [Ф] = Вебер (Вб);.1 Вб = 1 Тл·м². Відсутність в природі магнітних зарядів і той факт, силові лінії індукції магнітного поля замкнуті, приводять до теореми Гаусса для потока магнітной індукції - магнітний потік скрізь довільну замкнуту поверхню рівний нулю

(4.16)

Чи в диференціальній формі

div = 0 (4.17)

Тоді робота по переміщенню провідника з струмом в магнітному полі (4.13) буде у вигляді:

A = IdТ. (4.18)

Робота по переміщенню замкнутого контура з струмом в магнітному полі:

A = I (dТ₂ - dФ₁), (4.19)

де (dФ₂ - dФ₁) – зміна магнітного потоку крізь поверхню

Магнітне поле, володіючи замкнутими силовими линіями, називається вихровим. Циркуляціей вектора по замкнутому контуру називають інтегралом виду де - элемент довжини контура; - кут між векторами і . Для розрахунку магнітних полів постійнного струму в вакуумі використовується закон повного струму: циркуляція вектора магнітной індукції по довільному замкнутому контуру пропорційна алгебраїчній сумі струмів цього контуру:

. (4.20)

Тут N - число всіх провідників . При цьому струм рахується позитивним, якщо з кінца вектора I обхід контура l проходить проти часової стрілки; в протилежному випадку струм рахується негативним. Струми які не охоплюються контуром l , не дають вкладу в циркуляцію , а кожний струм в (4.20) застосовується стільки разів, скільки він охоплюється контуром. Наприклад, для системи струмів, зображених на рис. 4.8, отримаємо

.

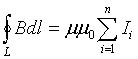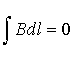1.8 Скористаємось законом повного струму для розра-хунку магнітного поля соленоїда і тороїда. а) знайдемо циркуляцію вектора В вздовж замкнутого контуру ABCD (рис.1). У нашому випадку витки в соленоїді щільно прилягають один до одного. Соленоїд має довжину, значно більшу за Рис.1 . На ділянках DA і BC  ; Тут  а На ділянці CD 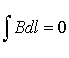; Цю ділянку можна вибрати досить далеко від соленоїда, де магнітне поле відсутнє. Тому з урахуванням цих зауважень маємо: .                                         (1.4) де N – число витків, які вкладаються в інтервалі довжини соленоїда АВ; І – струм, який протікає в цих витках. Але  , де l = AB. Закон повного струму в цьому випадку перепишеться: .                                            (1.5) Звідки індукція магнітного поля на осі довгого соленоїда буде дорівнювати: .                                             (1.6) Вираз (13.1.6) показує, що на осі довгого соленоїда зі струмом І індукція магнітного поля дорівнює: В = ₀nI.

б) магнітне поле на осі тороїда. Розглянемо тороїд, який має вигляд довгого соленоїда, кінець і початок якого збігаються (рис.13.2).   Рис.2 Витки в такій котушці щільно прилягають один до одного, а радіус осьової лінії R. Знайдемо циркуляцію вектора  вздовж осьової лінії тороїда , де N - число витків у тороїді; І - струм у витках. Але  - довжина кола вздовж осьової лінії, тому , де  - число витків на одиницю довжини осьової лінії тороїда. Таким чином, індукція магнітного поля на осі тороїда визначається такою ж формулою, що і для довгого соленоїда, тобто В = ₀nI .                  (1.7)

1.9 Магнітне поле - особлива форма матерії, через яку здійснюється взаємодія між рухомими електрично зарядженими частинками.

Для дослідження магнітного поля використовують рамку зі струмом. При цьому напрям вектора магнітної індукції визначають за правилом свердлика: якщо напрям поступального руху свердлика збігається з напрямом струму в провіднику, то напрям обертання ручки свердлика збігається з напрямом вектора магнітної індукції.

Рамка зі струмом у магнітному полі повертається внаслідок дії поля спочатку на кожну ділянку рамки зі струмом. До такого висновку вперше дійшов 1820 року французький фізик Ампер. Провівши багато дослідів, він встановив закон, названий його іменем,

F_A = BIlsina.

Сила Ампера F_A дорівнює добутку модуля вектора магнітної індукції на силу струму I, довжину ділянки провідника l і на синус кута a між вектором і напрямом струму.

Напрям сили Ампера визначають за правилом лівої руки (рис. 4.4.5). Якщо ліву руку розташувати так, щоб перпендикулярна до провідника складова вектора магнітної індукції входила в долоню, а чотири витягнутих пальці були напрямлені так само, як струм, то відігнутий на 90° великий палець покаже напрям сили, що діє на відрізок провідника.

Закон Ампера використовують для розрахунку сил, що діють на провідники зі струмом, у багатьох технічних пристроях, зокрема в електродвигунах.

Дія магнітного поля на провідник зі струмом є результатом дії поля на рухомі заряджені частинки всередині провідника.

Силу, яка діє на кожен рухомий заряд з боку магнітного поля, називають силою Лоренца. Її можна знайти за допомогою сили Ампера:

,                                                                   (4.4.1)

де N - кількість вільних носіїв заряду в провіднику.

Розглянемо ділянку провідника зі струмом (рис.4.4.6). Нехай його довжина Dl і площа поперечного перерізу S настільки малі, що індукцію магнітного поля можна вважати незмінною в межах провідника. Сила струму в провіднику згідно з формулою (4.2.1)

.                                                             (4.4.2)

З урахуванням рівняння (4.4.2) сила Ампера:

,                                          (4.4.3)

де nSDl = N - кількість вільних носіїв заряду.

Підставивши вираз для сили Ампера (4.4.3) у формулу (4.4.1), знаходимо вираз для сили Лоренца:

;

,

де a - кут між векторами швидкості вільних носіїв заряду і магнітної індукції.

Напрям сили Лоренца, як і напрям сили Ампера визначається за допомогою правила лівої руки (рис.4.4.7). Якщо ліву руку розмістити так, щоб складова магнітної індукції , перпендикулярна до швидкості заряду, входила у долоню, а чотири пальці були напрямлені за рухом позитивного заряду (проти руху негативного), то відігнутий на 90? великий палець покаже напрям сили Лоренца F_л, що діє на заряд.

Оскільки сила Лоренца перпендикулярна до швидкості частинки, то вона не виконує роботу. Згідно з теоремою про кінетичну енергію це означає, що вона не змінює кінетичної енергії частинки і, отже, модуля її швидкості. Під дією сили Лоренца змінюється лише напрям швидкості частинки. Якщо частинка влітає перпендикулярно до вектора магнітної індукції, то в магнітному полі вона буде рухатися по колу (рис.4.4.8). Якщо частинка влітає під кутом , то вона далі в магнітному полі буде рухатися по спіралі (рис.4.4.9).

 1.10 а) Оскільки магнітне поле вивчається за допомогою рамки із струмом- по орієнтуючій дії магнітного поля на рамку, то домовились визначати положення рамки в просторі з допомогою вектора , перпендикулярного до площини рамки (нормаль до рамки).

За додатній напрямок нормалі до рамки приймають нормаль, зв’язану зі струмом правилом свердлика (рис.2).

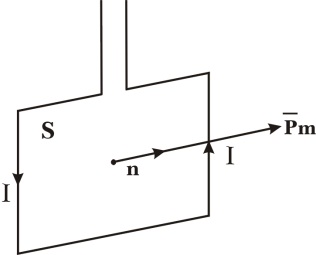
Рис. 2

Для визначення напрямку магнітного поля рамки розміщують в полі і дають їй можливість вільно повертатись і зайняти в просторі таке положення, при якому обертальний момент дорівнює нулю і рамка знаходитиметься в положенні стійкої рівноваги. Тоді напрям нормалі до рамки співпадає з напрямком магнітного поля ( ).

Обертальний момент пари сил, що діє на рамку з струмом в магнітному полі дозволяє використати її для кількісної характеристики поля. Розглянемо, які властивості рамки впливають на обертальний момент.

Досліди показують, що обертальний момент М має максимальне значення, якщо нормаль рамки перпендикулярна до магнітного поля. Крім цього обертальний момент М пропорційний силі струму в рамці І , та площі рамки S, тобто

Величину P_m=I·S називають магнітним моментом рамки із струмом. Отже

М~P_m

Магнітний момент рамки із струмом – величина векторна. Напрям вектора співпадає з напрямком нормалі (рис.2).

Б) Розглянемо струмопровідний контур прямокутної форми, одна сторона якого перебуває в магнітному полі.

– струм в контурі. На нього діє сила і він переміщується. На шляху його сторона описує площу:

Малюнок 63. Замкнений виток із струмом в магнітному полі.

При русі контуру із струмом електромагнітна сила на шляху виконує роботу:

(168)

Магнітний потік крізь поверхню окреслену провідником, є різницею потоків що пронизують контур в кінцевому та початковому положеннях:

Робота витрачена на переміщення контуру:

(169)

Висновок:

1) Робота електромагнітних сил, витрачена на переміщення контуру зі струмом, дорівнює добуткові струму в контурі на зміну магнітного потоку, зчепленого з контуром.

2) Усякий контур зі струмом у магнітному полі намагається зайняти положення, при якому магнітний потік, що пронизує контур, виявляється найбільшим.

(Електромагніти, реле).

3) При визначенні роботи, здійснюваної електромагнітними силами, було взято рамку, що має один виток.

Якщо рамку взяти з кількома витками, то робота збільшиться.

Припустимо ми взяли рамку яка має витків. Тоді:

Добуток кількості витків і зчепленого з цими витками магнітного потоку називають потокозчепленням.

(170)

(171)

Отже, робота електромагнітних сил виражається добутком струму в витках і приросту магнітного потокозчеплення:

(172)

Якщо у відокремленому контурі будь-якої форми є струм, то його магнітне поле зчеплене із самим контуром.

1.11 Якщо частинка влітає перпендикулярно до вектора магнітної індукції, то в магнітному полі вона буде рухатися по колу (рис.4.4.8). Якщо частинка влітає під кутом , то вона далі в магнітному полі буде рухатися по спіралі (рис.4.4.9).

 

2.1 При вивченні магнітного поля в речовині (магнетику) розрізняють два типи струмів: макроструми і мікроструми. Макрострумами називають електричні струми провідності, а також конвекційні струми, які зв’язані з рухом заряджених макроскопічних тіл. Мікрострумами, або молекулярними струмами, називаються струми, які зумовлені рухом електронів в атомах, іонах і молекулах.

Магнітне поле в речовині складається з двох полів: зовнішнього поля , яке створюється макрострумами, і внутрішнього поля , яке створюється молекулярними струмами. Вектор магнітної індукції результуючого магнітного поля в речовині дорівнює векторній сумі магнітних індукцій зовнішнього і внутрішнього полів:

.

Вектор залежить від магнітних властивостей речовини.