4. Виды таблиц по характеру подлежащего

По содержанию подлежащего все статистические таблицы можно разделить на следующие группы:

1) Простые таблицы, в подлежащем которых отсутствуют группировки. Они содержат обобщающие показатели, относящиеся к перечню единиц совокупности (перечневые таблицы (табл.1)), к перечню хронологических дат (хронологические таблицы (табл. 2)) или к перечню территорий (территориальные таблицы (табл. 3)).

Таблица 1. Перечневая таблица [3, c. 54]

Подлежащее – марка бензина.

Таблица 2. Простая перечневая таблица по временному принципу [3, c. 57]

Цифры условные

Подлежащее – годы.

Таблица 3. Простая перечневая таблица по территориальному признаку [3, c. 58] (Шмойлова 57)

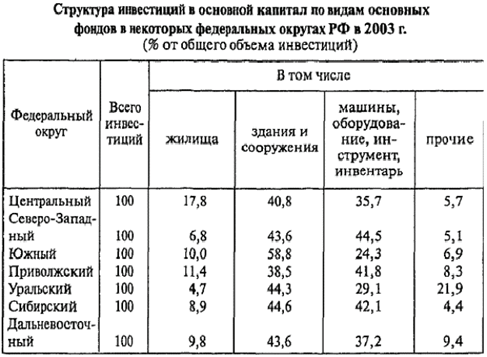
Подлежащее – перечень федеральных округов.

2) Групповые таблицы (табл. 4), в подлежащем которых изучаемый объект разделен на группы по определенному признаку. При этом каждая группа может быть охарактеризована рядом показателей.

Таблица 4. Групповая таблица [3, c. 58]

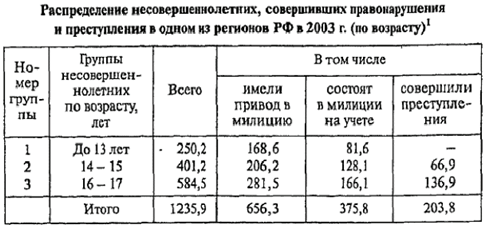
1 Цифры условные

Подлежащее – группы несовершеннолетних, совершивших правонарушения и преступления по возрасту

3) Комбинационные таблицы (табл. 5), в подлежащем которых дана группировка единиц совокупности по двум и более признакам, взятым в комбинации.

Таблица 5. Сложная комбинационная таблица [3, c. 58]

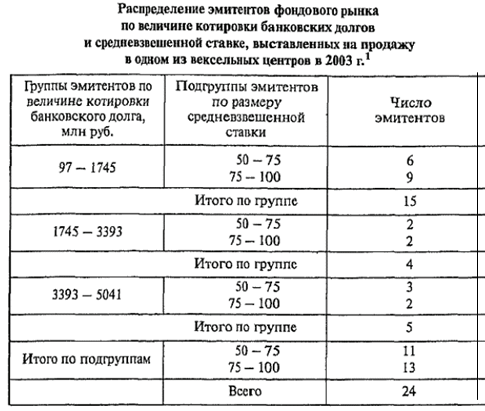
1 Цифры условные. Подлежащее – группы элементов фондового рынка, распределенных по величине котировки банковских долгов и средневзвешенной ставке [3, c. 59].

5. Виды таблиц по характеру сказуемого

Система показателей, которыми характеризуется объект изучения, т.е. подлежащее таблицы, образует сказуемое статистической таблицы. Сказуемое формирует заголовки граф и составляет их содержание.

По структурному строению сказуемого различают статистические таблицы с простой и сложной его разработкой. При простой разработке сказуемого показатель, его определяющий, получается путем простого суммирования значений по каждому признаку отдельно независимо друг от друга (табл. 4). Сложная разработка сказуемого предполагает деление признака, его формирующего, на группы (табл. 6).

Таблица 6. Распределение клиентов страховых компаний по категориям и страховым суммам в I квартале 2003 г. [3, c.60]

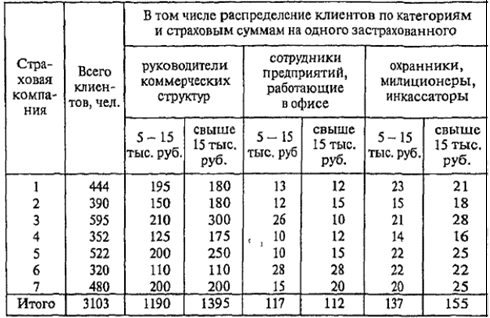
1 Цифры условные

Статистическая таблица со сложной комбинированной разработкой сказуемого содержит два связанных между собой признака: атрибутивный – качественный – категории застрахованных и количественный – страховая сумма [3, c. 60].

Задача № 6

При изучении покупательского спроса на обувь зарегистрирована продажа следующих размеров детских ботинок:

34	32	33	31	33	34	33
32	34	34	32	33	34	31
33	32	31	33	34	33	34
34	34	32	34	33	32	33
33	33	34	34	34	34	34
31	32	31	33	32	33	32
32	33	34	33	33	34	33
33	32	31	34	31	33	34
34	34	32	31	34	32	32
34	31	34	33	33	34	34
32	33	34	33	33	34	33
33	32	31	34	31	33	34
34	34	32	31	34	32	32
34	31	34	33	33	34	34
34	32	33	31	33	34	33
32	34	34	32	33	34	31
33	32	31	33	34	33	34
34	34	32	34	33	32	33
33	33	34	34	34	34	34
31	32	31	33	32	33	32

1 Для обобщения данных реализованного спроса постройте ряд распределения и проанализируйте полученные результаты, сравнив их с типовой шкалой поставки обуви в магазин.

Размер	31	32	33	34	Всего
Число пар к итогу, %	22	24	26	28	100

2. Данные распределения покупательского спроса и типовой шкалы поставки обуви изобразите на графике.

3. Укажите модальную и медианную величины ряда распределения.

4. Результаты разработок изложите в таблице. Сделайте выводы о соответствии предложения обуви покупательскому спросу.

Решение:

Размер	31	32	33	34	Всего
Число пар	18	28	42	52	140
Число пар к итогу, %	12,86	20,00	30,00	37,14	100

Сравним полученные данные с типовой шкалой поставки обуви в магазин.

Размер	31	32	33	34	Всего
Число пар к итогу факт, %	12,86	20,00	30,00	37,14	100
Число пар к итогу типовая шкала, %	22	24	26	28	100
Отклонение, +,-	-9,14	-4	4	9,14	0

Таким образом, по сравнению с типовой шкалой на обувь 31 размера и 32 размера спрос был в меньшей доле (на 9,14 процентных пункта и 4 процентных пункта соответственно), а на обувь 33 размера и 34 размера в большей доле – на 4 процентных пункта и 9,14 процентных пункта соответственно.

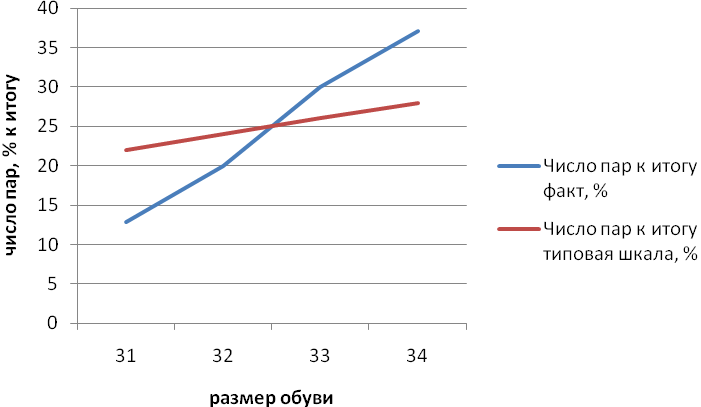
Рисунок 1 - Данные распределения покупательского спроса и типовой шкалы поставки обуви

Модальная величина – обувь 34 размера.

Медианная величина – обувь 33 размера.

Таким образом, мы видим, что предложение обуви не соответствовало спросу, предприятием был переоценен спрос на обувь 31 и 32 размера и недооценен спрос на обувь 33 и 34 размеров.

ЗАДАЧА № 7

Используя построенный в задаче № 6 ряд распределения магазинов определите:

- среднее квадратическое отклонение;

- коэффициент вариации;

- модальную величину.

- медианную величину.

Постройте гистограмму распределения и сделайте выводы.

Решение:

Определим среднее квадратическое отклонение

Размер (х)	31	32	33	34	Всего
Число пар	18	28	42	52	140
х-хср	-2	-1	0	1	-2
(х-хср)2*m	72	28	0	52	152

Средний размер обуви определим так:

(31*18+32*28+33*42+34*52)/140=32,91≈33.

σ²=

σ²=152/140=1,08

σ=1,04.

v= σ/ *100%

v=1,08/33*100=3,27%.

Таким образом, исследуемая совокупность однородная.

Модальная величина – обувь 34 размера.

Медианная величина – обувь 33 размера.

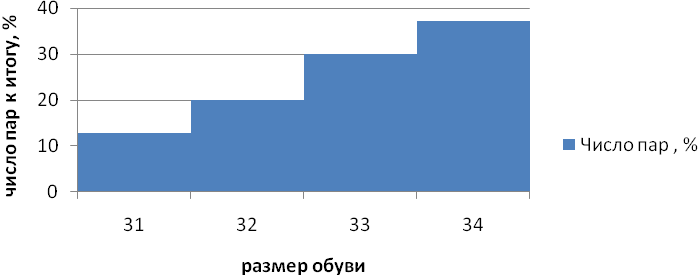
Рисунок 2 – Гистограмма распределения

ЗАДАЧА № 8

Имеются данные о численности (среднесписочной) работников предприятия за 2000 – 2005 гг.:

Годы	2000	2001	2002	2003	2004	2005
Численность работников, (чел.)	1215	1100	1280	1320	1370	1440

На основе этих данных:

1. Для анализа динамики численности работников предприятия за 2000 – 2005 гг. вычислите следующие показатели динамики:

1. абсолютный прирост (на цепной и базисной основе);

2. темпы роста и прироста (цепные и базисные);

3. средний абсолютный прирост и средний темп прироста.

Интенсивность развития ряда динамики изобразите графически.

2. Произведите анализ общей тенденции развития численности работников:

1. фактические и теоретические уровни ряда динамики нанесите на график;

2. используя полученную модель, рассчитайте возможную численность работников в 2007 г.

Решение:

Для расчетов воспользуемся следующими формулами:

Таблица 2 – Формулы для расчетов

Абсолютные и относительные показатели динамики
Темп прироста		Tn=(Kp-1)100 Tn=Tp-100 Tn=(/yi-1)100	Tn=(Kp-1)100 Tn=Tp-100 Tn=(/y0)100
Абсолютное значение 1% прироста		A=/Tn A=Yi-1/100	A=/Tn A=Y0/100
Средние показатели динамики
Средний уровень ряда динамики В интервальном ряду: с равностоящими уровнями
Средний абсолютный прирост
Средний коэффициент роста

Для удобства проведения расчетов составим табл.3.

Таблица 3 – Вспомогательный расчет

Годы	2000	2001	2002	2003	2004	2005	Среднее значение
Численность работников, (чел.)	1215	1100	1280	1320	1370	1440	1287,5
Абсолютный прирост цепной, чел.		-115	180	40	50	70	45
Абсолютный прирост базисный, чел.		-115	65	105	155	225	87
Коэффициент роста цепной		0,9053	1,1636	1,0313	1,0379	1,0511	1,0346
Коэффициент роста базисный		0,9053	1,0535	1,0864	1,1276	1,1852
Темп роста цепной, %		90,53	116,36	103,13	103,79	105,11	103,46
Темп роста базисный, %		90,53	105,35	108,64	112,76	118,52	1287,5
Темп прироста цепной, %		-9,47	16,36	3,13	3,79	5,11	45
Темп прироста базисный, %		-9,47	5,35	8,64	12,76	18,52
Абсолютное значение 1% прироста		-1,27	1,55	0,39	0,48	0,67	13,02

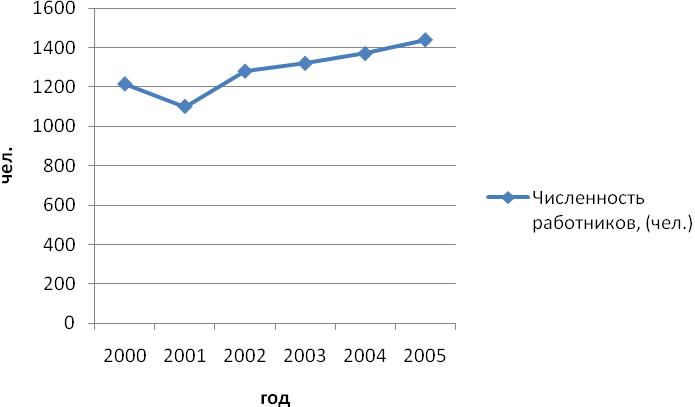
Рисунок 1 – Динамика численности работников в 2000-2005гг

Используя метод наименьших квадратов, находим уравнение зависимости:

,

где у – это уровни эмпирического ряда;

n – количество уровней ряда;

t – время.

Эту систему можно упростить, если отсчет моментов ведется от середины ряда. При четном числе уровней ряда предшествующие периоды обозначаются так: -1, -2, -3…, а последующие за серединным периодом через +1, +2, +3…

а= ; а=7725/6=1287,5

b= ; b=1255/28=44,82

Таблица 4 – Выявление основной тенденции с помощью метода аналитического выравнивания

Годы	Численность работников, чел.	t	t2	у*t	у расч
2000	1215	-3	9	-3645	1153
2001	1100	-2	4	-2200	1198
2002	1280	-1	1	-1280	1243
2003	1320	1	1	1320	1332
2004	1370	2	4	2740	1377
2005	1440	3	9	4320	1422
Итого	7725	0	28	1255	7725

=1287,5+44,82*t

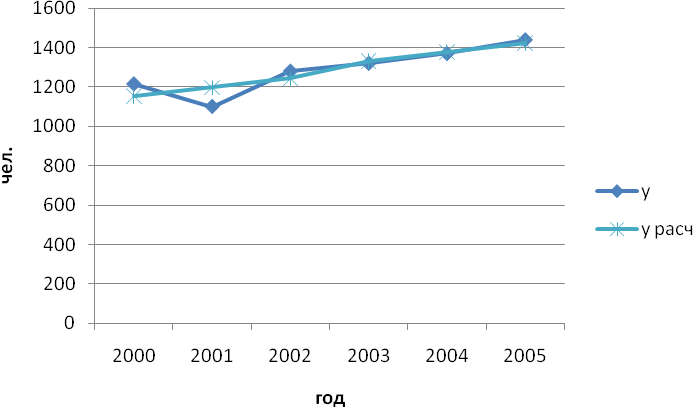
Рисунок 2- Фактические и теоретические уровни ряда динамики

Используя построенную модель, произведем прогнозирование численности работников в 2007г;

у²⁰⁰⁷=1287,5+44,82*5=1512 чел.

ЗАДАЧА № 9

Реализация продукта «Т» на рынках города характеризуется за два периода следующими данными:

Рынок	Модальная цена (руб. за 1 кг)		Количество (т)
	август	ноябрь	август	ноябрь
1	2	3	4	5
1	33,28	42,03	145	120
2	30,44	45,20	182	148
3	36,82	44,36	112	110
4	31,48	39,80	210	175
Итого:			649	553

Определите:

1. Индексы цен: переменного и постоянного состава.

2. Индекс влияния структурных сдвигов.

3. Прирост средней цены в абсолютных величинах – общий и за счет действия отдельных факторов.

Покажите взаимосвязь исчисленных индексов. Сделайте выводы по полученным результатам.

Решение:

Решение 

а) индекс цен переменного состава 

Рассчитаем средние цены: 

Средняя цена за отчетный период 

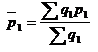
Средняя цена за базисный период 

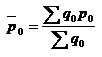
Рынок
1	4825,6	5043,6	3993,6
2	5540,1	6689,6	4505,1
3	4123,8	4879,6	4050,2
4	6610,8	6965,0	5509,0
Итого	21100,3	23577,8	18057,9

Из этих формул следует, что средняя цена по всем группам зависит от средней цены по отдельным группам и доли физического объема продаж в каждой из этих групп.

=23577,8/553=42,64

=21100,3/649=32,51

Индекс цен переменного состава составит:

Iп.с.=42,64/32,51=1,31

Итак, за счет влияния всех факторов цена возросла на 31%.

Индекс цен фиксированного (постоянного) состава рассчитывается по формуле:

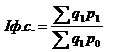
Iф.с.= 23577,8/18057,9=1,31

За счет изменения структуры цены средняя цена возросла на 31% 

в) индекс влияния изменения структуры производства продукции на динамику средней цены 

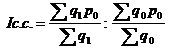
Ic.c.=18057,9/553: 21100,3/649=1

Сравнивая формулы, полученные для расчета вышеуказанных индексов, нетрудно заметить, что индекс структурных сдвигов равен отношению индекса переменного состава и индекса фиксированного состава, т.е.: 

Ic.c.= Iп.с./ Iф.с.

Ic.c.=1,31/1,31=1.

Прирост средней цены в абсолютных величинах – общий и за счет действия отдельных факторов.

Абсолютный прирост цен можно рассчитать так:

Δр= -

Δр=42,64-32,51=10,13 руб.

Изменение средней цены на крахмал по всем группам только за счет изменения средней цены по отдельным группам будет рассчитываться по формуле: 

Δ =42,64-18057,9/553=9,99 руб.

Аналогичные рассуждения проводятся и для расчета изменения средней цены по всем группам только за счет изменения структуры физического объема: 

Δ =18057,9/553-32,51=0,14 руб.

Таким образом, общее изменение цен на 10,13 руб. произошло за счет изменения средней цены по отдельным группам на 9,99 руб. и за счет изменения средней цены по всем группам только за счет изменения структуры физического объема – на 0,14 руб.

ЗАДАЧА № 10

Имеется следующая информация о деятельности торгового дома за два периода:

Товарные группы	Продано товаров в сопоставимых ценах (тыс. руб.)		Среднее изменение цен (%)
	Январь	Март
1	2	3	4
А	1200	2300	+150
Б	800	1800	+250
В	650	1900	+190
Г	1200	2650	+165
Д	1300	2900	+130

Определите:

1. Индивидуальные и общие индексы: цен, физического объема и товарооборота; покажите их взаимосвязь

2. Прирост товарооборота в марте по сравнению с январем (общий и за счет действия отдельных факторов).

Сделайте выводы по полученным результатам.

Решение:

Определим индивидуальные индексы

Взаимосвязь индексов выглядит следующим образом:

i_pq= i_p* i_q

Таблица 2 – Индивидуальные индексы цен, физического объема, товарооборота

Товары	ipq	ip	iq
А	1,92	2,50	0,77
Б	2,25	3,50	0,64
В	2,92	2,90	1,01
Г	2,21	2,65	0,83
Д	2,23	2,30	0,97

Рассчитаем общий индекс товарооборота по следующей формуле:

I_pq=

Товары
А	1200	2300	920
Б	800	1800	514
В	650	1900	655
Г	1200	2650	1000
Д	1300	2900	1261
Итого	5150	11550	4350

I_pq=11550/5150=2,24

Таким образом, за счет влияния всех факторов произошло увеличение товарооборота в 2,24 раза или на 124%.

Общий индекс цен определяется по следующей формуле:

I_p=

I_p=11550/4350=2,66

Таким образом, за счет изменения цен произошло увеличение товарооборота на 166%.

Общий индекс физического объема продаж определяется следующим образом:

I_q=

I_q=4350/5150=0,84.

Таким образом, за счет изменения физического объема произошло снижение товарооборота на 16%.

Проверка:

0,84*2,66=2,24.

Определим прирост товарооборота в марте по сравнению с январем (общий и за счет действия отдельных факторов).

Общий прирост товарооборота

ΔТ=11550-5150=6400 тыс. руб.

Изменение товарооборота за счет изменения цен составит:

ΔТ(р)=11550-4350=7200 тыс. руб.

Таким образом, за счет изменения цен произошло увеличение товарооборота на 7200 тыс. руб.

Изменение товарооборота за счет изменения физического объема:

ΔТ(q)=4350-5150=-800 тыс. руб.

Таким образом, за счет изменения физического объема произошло снижение товарооборота на 800 тыс. руб.

Проверка: 7200-800=6400

Заключение

Статистические данные должны быть представлены так, чтобы ими было удобно пользоваться. Если включить множество цифра в текст, это затруднит их восприятие. Более эффективно представление статических данных в форме таблиц.

В отличие от математических таблиц умножения, тригонометрических функций, логарифмов и других, которые по начальным условиям позволяют получить тот или иной результат, статистические таблицы рассказывают языком цифр об изучаемых объектах.

Анализ данных статистических таблиц как метод научного исследования позволяет выявить соотношения и пропорции между группами явлений по одному или нескольким признакам, провести сравнительный анализ, охарактеризовать типы социально-экономических явлений, выявить характер и направление взаимосвязей и взаимозависимостей между различными, определенными логикой экономического анализа признаками, сформулировать выводы и определить резервы развития изучаемого явления, объекта или процесса.

Значение таблиц определяется тем, что они позволяют изолированные статистические данные рассматривать совместно, достаточно полно и точно охватывая сложную природу явлений.

Соблюдение правил построения и оформления статистических таблиц делает их основным средством представления, обработки статистической информации.

35